不同塑性条件对板料冲压成形有限元模拟分析

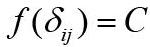
摘 要：本文主要通过有限元软件仿真了不同塑性条件对圆筒形零件冲压成形结果的影响，基于有限元分析软件Abaqus6.11，在零件毛坯和外界条件参数除材料属性以外设置相同的情况下，分别采用Mises屈服准则、Tresca屈服准则和Hill屈服准则进行模拟试验，得到不同的分析结果，并进行对比。

关键词：塑性条件;冲压成形;Mises屈服准则;Tresca屈服准则;Hill屈服准则

1引言

板料冲压成形在汽车、航空航天、石油化工等诸多领域均有广泛的应用。例如，汽车车身覆盖件、大油罐等的成形均采用板料冲压工艺。板料成形过程包括了非常复杂的物理现象，涉及力学中的三大非线性问题：几何非线性、物理非线性和边界非线性，因此，难以用传统的弹塑性理论的解析方法进行研究。随着计算机技术的迅速发展及有限元方法的成熟，特别是商用有限元软件的不断完善，促进了板料成形中数值模拟技术的发展。

有限单元法是当前工程技术领域中最常用最有效的数值计算方法。有限元法的基本思想是把连续体视为离散单元的集合体来考虑。在应用有限元法分析问题时，首先采用“化整为零”的办法，将连续体分解为有限个性态比较简单的“单元”，对这些单元分别进行分析;然后采用“积零为整”的办法，将各单元重新组合为原来的连续体的简化了的“模型”，通过求解这个模型得到问题的基本未知量（例如位移）在若干离散点上的数值解;最后，根据得到的数值解再回到各个单元中计算其他物理量（例如应变、应力）。

塑性条件又称屈服条件或屈服准则，它是变形体由弹性状态向塑性状态过渡的力学条件。或者把在不同应力状态下，变形体某点进入塑性状态并使塑性变形继续进行，各应力分量与材料性能之间必须符合一定的关系，这种关系称为屈服准则。一般可表示为

式中是应力分量的函数，对于各向同性材料，它是应力不变量的函数。C是与材料性质有关的常数，通过试验测得。

屈服准则有很多种，例如，Mises屈服准则、Tresca屈服准则、Hill屈服准则等，在工程实际中需要根据不同的材料性质选用。本文通过使用有限元分析软件Abaqus6.11比较Mises屈服准则、Tresca屈服准则和Hill屈服准则对板料冲压成形的影响，来说明三者的区别。

2计算模型，材料参数和边界条件

板料冲压过程是一个非常复杂的塑性成形过程，许多因素都直接或间接地影响着成形的结果。本文以实际生产中常见的板料冲压成形过程为例，利用Abaqus6.11对该成形过程进行了模拟计算。Abaqus 是一款优秀的有限元分析软件，它可以针对不同操作系统进行单机或多机并行运算，缩短开发设计时间，而且模拟的结果与实际结果相距不大，大大节省了产品设计开发的成本。在外界条件参数设置相同的情况下，分别采用典型的各向同性塑性条件Mises 屈服准则、Tresca屈服准则和各向异性塑性条件Hill屈服准则对板料冲压成形进行对比。

2.1零件的CAD模型和有限元模型

板料与凸模间摩擦系数为0.1，与凹模间摩擦系数为0.1，板料厚度为2mm。模具参数为：凸模直径56mm，凸模圆角8mm，凹模直径60mm，凹模圆角8mm。模型如下图1所示。

在有限元分析过程中，可以充分利用结构的对称性对问题进行简化，将部分结构作为有限元分析对象，降低分析过程的复杂度，减少工作量。具有轴对称结构，若载荷也对称，可取其中的一半作为分析对象，如果对于X、Y轴都对称，只需将四分之一作为分析对象。在Abaqus6.11中分别建立板料冲压模具（包括凸模、凹模、压边圈）以及成形板料的简化模型。

所做简化主要包括：1凸模、凹模、压边圈简化。由于在板料冲压成形过程中，模具的刚性通常远远大于板料的刚性，因此模具的变形相对板料变形来说极小，可忽略不计。它们三个都是刚性体，在冲压过程中不发生变形，故可简化其为一个面。2作用于板料上的外力主要有三个来源，压边圈对板料的作用力;凸模对板料的作用力;凹模对板料的作用力。上述作用力中有包括法向接触力和切向摩擦力，切向摩擦力与法向接触力和接触表面摩擦系数有关。此外板料还受到重力作用，但由于重力作用在板料上的接触力和摩擦力较小，可忽略不计。3忽略冲压过程的热效应。4采用库伦摩擦模型，不考虑接触面上的粘合现象，即摩擦力与接触面上的正压力成正比，且摩擦只发生在在模具与工件的界面，摩擦系数在冲压过程中保持不变。简化模型如图2所示。

2.2定義材料属性

在ABAQUS/CAE中材料屈服准则默认为Misses屈服准则，也就是默认材料为各向同性材料，因此我们在材料属性定义模块中定义各向同性的材料banliao，包括材料的密度7.85E-9、杨氏模量210000、泊松比0.3;并定义塑性应力应变关系，如图3所示。

2.3 定义分析步

添加成形分析步，类型设置为动态显示分析步，定义板材的厚度为2mm。

2.4 定义接触

定义成形过程中的接触属性，包括板材和压边圈的接触摩擦系数、板材和凸模的接触摩擦系数、板材和凹模的接触摩擦系数，均设定为0.1。

2.5 定义载荷及边界条件

定义凸模参考点、压边圈参考点、凹模参考点和对称边界约束，图4所示。

在压边圈上设置集中载荷100KN，方向为竖直向下;将凹模的六个自由度全部约束，压边圈、凸模除竖直向下的平移自由度外其余五个自由度均设置约束;板材的两个直角边设置对称约束;为凸模添加位移约束，冲压方向竖直向下，位移为80mm。

2.6 划分网格

因为凸模、凹模和压边圈作刚体处理，所以划分较大网格，板材需要做塑性变形分析，所以划分较小网格，单元类型选择S4R。最终划分网格如图5所示。

3不同塑性条件对比及结果分析

3.1 Mises屈服准则

该屈服准则由德国力学家Mises于1913年提出的，可以表述为：在一定的变形条件下，当受力物体内一点的应力张量的第二不变量达到某一定值时，该点就进入塑性状态，即。所以，

式中，σ1、σ2和σ3是该点的三个主应力，K是与变形条件下的材料性质有关而与应力状态无关的常数，可以通过均匀拉伸试验求得。

并且，如果Mises屈服条件成立，则拉伸屈服极限与剪切屈服极限之间应满足以下关系

由于这一屈服条件只用一个式子表示，易于数学处理，而且可以不必求出主应力，故使用简便。

将Abaqus中建立好的有限元模型进行提交运算，Abaqus计算得到的板料应力云图，如图6所示。

3.2 Tresca屈服准则

1864年法国工程师屈雷斯加在金属挤压试验中首先发现材料的屈服与最大切应力有关。即当变形体（质点）中的最大切应力达到某一定值时，材料就发生屈服。或者说材料处于塑性状态时，其最大切应力是一不变的定值，该定值只取决于材料在变形条件下的性质，而与应力状态无关。所以该准则又称为最大切应力不变准则。

若规定时，则最大切应力为

所以Tresca准则可以写成：

式中常数C可通过试验求得。由于C值与应力状态无关，故可用最简单的单向拉伸试验来确定C值。Abaqus6.11计算得到的板料应力云图，如图7所示。

3.3 Hill屈服准则

针对各向同性材料来说，Tresca和Mises屈服准则虽然理论上能在假设无包申格效应的情况下用于应变硬化材料。但是，初始为各向同性材料受到塑性变形时，由于滑移机理的特征，结晶轴有趋势转到最合适的方位。因此，塑性变形时，材料有增加各向异性的趋势。

Hill屈服准则是Mises屈服准则的一个简单的扩展，可以描述各项异性材料的屈服，Hill建议用应力张量δij的分量来表示各向异性材料的屈服准则，用直角笛卡尔应力分量表示为

式中F、G、H、L、M和N是通过不同方向的材料实验得到的常数，如下：

式中R11、R22、R33、R12、R13和R23是各向异性屈服应力比，分别定义如下：

其中是当的做为位移应力分量加载时测量的屈服应力值，σ0用户在金属塑性定义中设置的参考屈服应力，。

在Abaqus6.11中创建各向异性材料Steel-Hill，并按照上面密度、杨氏模量、泊松比及塑性应力应变关系定义参数，应用Hill各向异性屈服准则需要在塑性子选项中定义各向异性屈服应力比R11=1.6974、R22=1.4956、R33=1、R12=1.2116、R13=1.35、R23=1.2116，如图8所示。将Abaqus6.11中建立好的有限元模型进行提交运算，计算完成后得到零件毛坯成形后状态的应力云图，如图9所示。

3.4 模拟结果对比

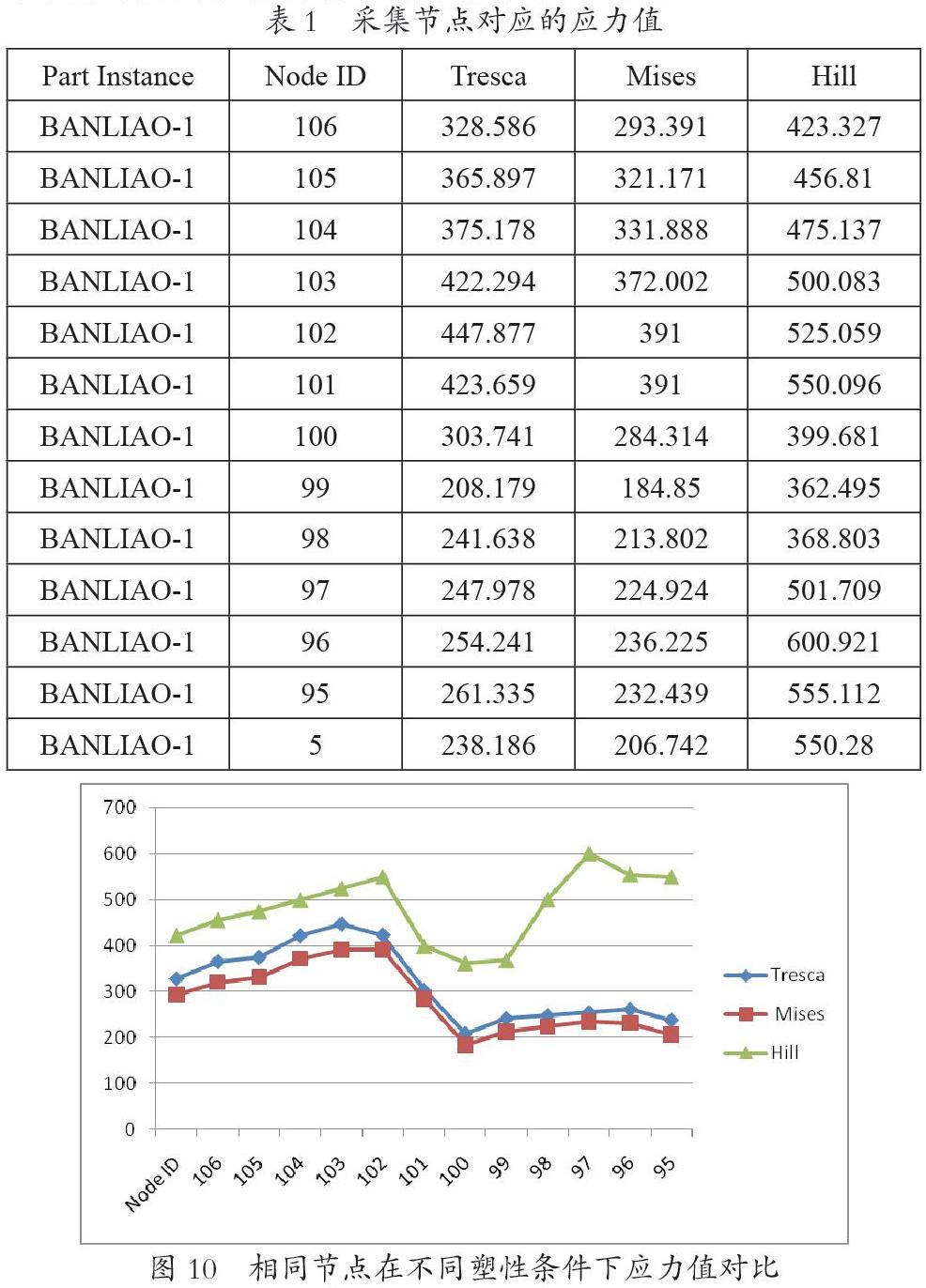
Hill屈服准则相比Mises屈服准则和Tresca屈服准则计算结果，可以看出应力分布有明显的区别。采集13个节点，得出不同节点处在三种不同屈服条件下的应力值，如表1所示;该采集得到13个节点对应不同屈服条件下的曲线图如图10所示。

由相同节点在不同塑性条件下应力值对比图，可以看到应用Mises屈服准则和Tresca屈服准则计算的结果的曲线趋势很接近。而Hill屈服准则的应力相比Tresca应力和Mises应力，整体水平偏大，而且其分布也不尽相同。

4结论

Mises屈服准则和Tresca屈服准则计算的结果很接近。实际上在有两个主应力相等的应力状态下两者分析结果是一致的。Tresca屈服准则没有考虑中间主应力的影响，三个主应力大小顺序不知时，使用不便;而Mises屈服准则考虑了中间主应力的影响，使用方便。

通过对比分析，可以得出在除屈服准则不同其他设置完全相同的情况下，板料在冲压成形后， Mises屈服准则和Tresca屈服准则应力分布与Hill屈服准则应力分布有很大不同。这说明了材料塑性条件的选择对板料塑性成形有限元模拟结果有很大影响，因而在进行模拟材料塑性变形有限元仿真时应该针对材料性质选择正确的材料属性和屈服準则，只有这样才能保证有限元仿真结果的准确。

参考文献：

[1]李宇、于盛睿、王文超、罗云龙、李成.基于板料冲压的有限元数值模拟.热加工工艺，2008，37（23）：61-64.

[2]朱向哲、林伟.影响板料冲压成形质量因素的有限元分析[J].辽宁石油化工大学学报，2005，25（2）：46-49.

[3]张朝志.影响板料冲压成形因素的有限元分析[J].辽宁省交通高等专科学校学报，2005，7（1）：44-46.

[4]董湘怀.轴对称及三维金属板料成形的有限元模拟.武汉：华中理工大学，1992.

[5]曾攀. 有限元分析及应用[M]. 北京： 清华大学出版社， 2004.

[6]俞汉清，陈金德. 金属塑性成形原理[M]. 机械工业出版社，2007年1月.

[7]刘展，祖景平，钱英莉，周华樟. ABAQUS6.6基础教程与实例详解[M]. 中国水利水电出版社，2008年2月.

[8]翟平，林兆荣. 飞机钣金成形原理与工艺[M]. 西安：西北工业大学出版社.

作者简介：

宋锦涛（1986—），男，汉族，陕西延安市人，本科，工程师，机械设计制造及其自动化，研究方向：机械设计制造检验和试验。