基于多传感器融合的机器人位姿估计研究

罗耀耀，钟 山，王 锐，王 楠，杨韵秋

（1.成都理工大学 核技术与自动化工程学院，四川 成都 610059；2.成都理工大学 信息科学与技术学院，四川 成都 610059）

随着人类社会的发展，自动驾驶技术与移动机器人领域成为当今社会研究热点，在移动机器人控制中，机器人定位与位姿估计是机器人研究的核心问题之一。受限于室内复杂环境，诸如GPS 等定位方法无法在室内使用，所以研究者多使用里程计，超声波等传感器完成位姿估计。

传统机器人室内定位一般采用里程计航迹推测或惯性导航定位等方法，如文献[1]利用惯性系统进行定位，但是其定位精度取决于初始位置，姿态信息的精确性以及推算过程中速度的航向信息求解。而且随着时间推移其累积误差很难消除，文献[2]在传统UMBmark 方法下改进校核系统参数，在一定情况下减小了编码器里程计方法进行航迹推测时的累积误差。但是对于车轮打滑等情况造成的漂移问题不能有效解决，累积误差随着时间增大。

为解决此类问题，有研究者采用超宽带（ultrawideband,UWB）技术定位[3]，通过脉冲无线电测距和测向，获得了比较好的定位精度，但是其受限于成本和频谱利用率，目前难以大规模使用。文献[4—5]提出的利用视觉传感器定位方法虽然也能避免累积误差的问题，但是其算法运算量极大，同时受限于视觉传感器性能，是当前的研究热点。Jaimez 等[6]提出RF2O方法，是一种利用激光雷达密集扫描的点云数据，制定范围流方程和几何约束获得运动估计的方法，该方法和视觉定位方法相似，数据处理量远小于视觉方法，所得位姿估计累积误差也较小，具有优异的性能。然而由于激光雷达的转动带来的角度误差，导致RF2O方法的定位存在一定的不确定性。

本文在RF2O 算法的基础上，针对移动机器人建立5 自由度的运动模型，寻求通过扩展卡尔曼滤波来融合激光雷达的数据和IMU 的偏航数据及Y 轴加速度数据[7-10]，进而解决因为激光雷达机械干扰带来的定位误差。

1 RF2O 方法及激光雷达介绍

RF2O 方法是一种快速精确的方法，仿照密集的3D 视觉测距法的方式，对激光雷达从二维平面扫描的密集点云数据进行处理。对点云数据制定基于传感器速度范围流约束方程，对所得几何约束的鲁棒函数最小化，获得运动估计。RF2O 方法运算量低于视觉方法，转换评估较为准确。但是由于激光雷达自身的旋转，会导致旋转不准确，本文通过RF2O 和IMU 的传感器数据融合解决这一问题。

激光雷达[7]是以发射激光束探测目标的位置、速度等特征量的雷达系统。其工作原理是向目标发射探测信号（激光束），然后将接收到的从目标反射回来的信号（目标回波）与发射信号进行比较，适当处理后，就可获得目标的有关信息，如目标距离、方位、高度、速度、姿态、甚至形状等参数。本文所使用激光雷达为镭神LS01G 型二维激光雷达，能在一个二维平面上进行扫描，并将扫描到的数据转换为点云数据，该激光雷达的主要参数如表1 所示。

表1 激光雷达参数

2 坐标系定义及姿态表示

本文坐标系为北东地坐标指向，设导航坐标系为Odom，车体中心坐标系为Base_link。坐标轴 XO，OY，ZO分别指向移动机器人前方、右方、上方。

移动机器人只在二维平面运动，所以在姿态解算时只用解算其偏航角，由姿态转换矩阵易得[11]：

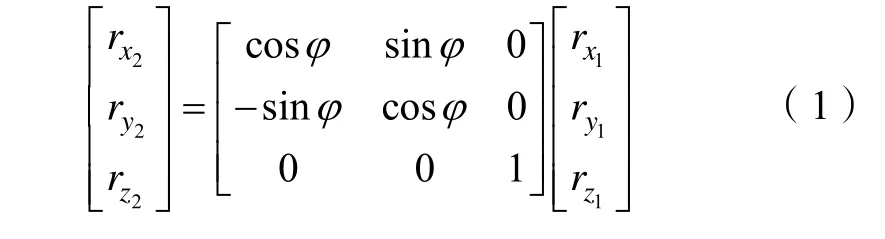
其中：2xr、ry2、rz2为空间矢量在Base_link 坐标系的投影，1xr、1yr、1zr 为在Odom 坐标系投影。φ 为绕Odom 坐标系Z 轴角度，式（1）记作：

3 系统运动学模型

为了确定移动机器人在Odom 下的位姿信息，建立Odom 坐标系与Base_link 坐标系之间的关系，如图1所示。

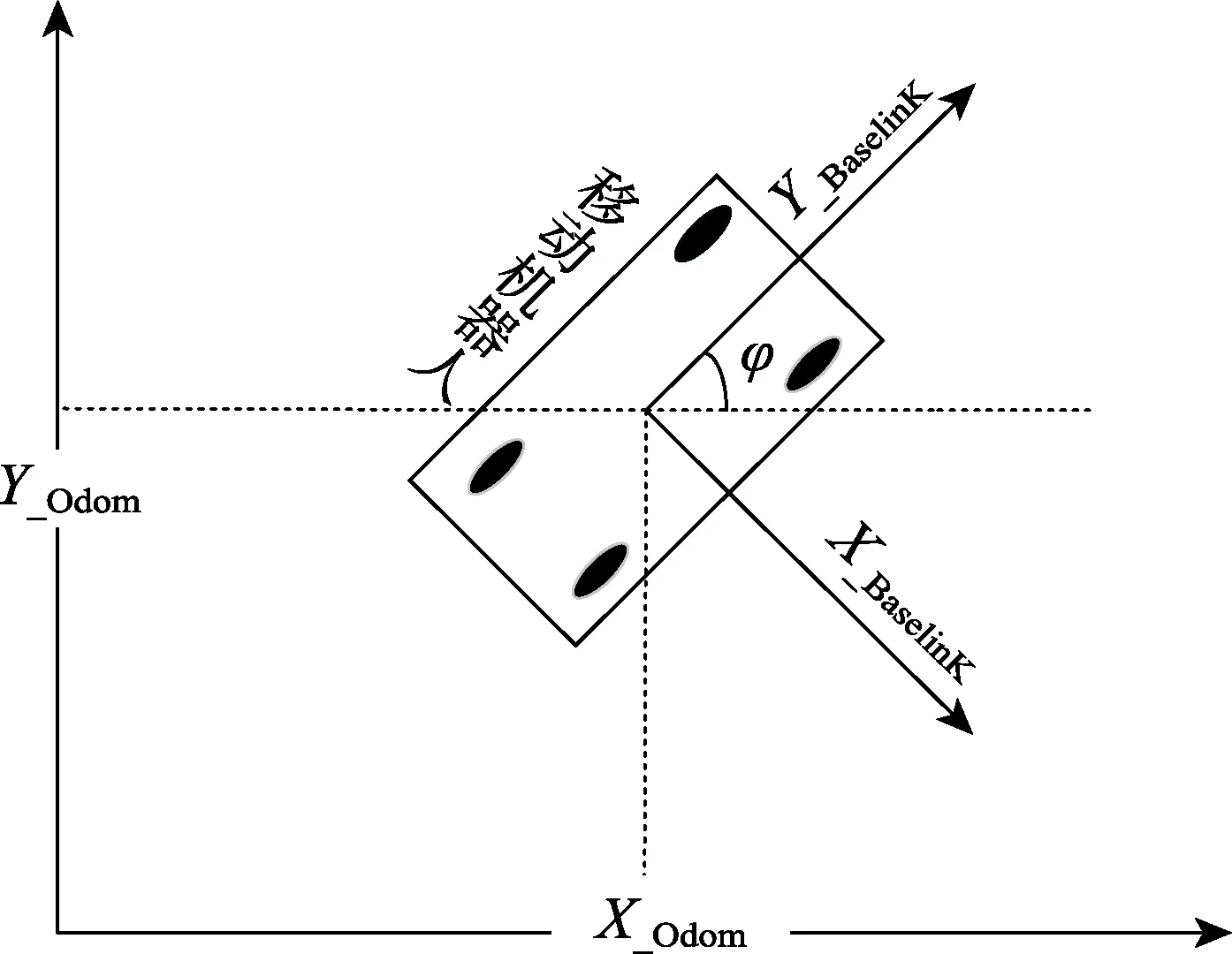
图1 位姿转换关系

X_Odom、Y_Odom、X_Baselink、Y_Baselink分别为Odom坐标系和Base_link 坐标系的坐标轴。由于移动机器人在近似二维平面上运动，所以其在Odom 坐标系的位姿可以用点 P(x, y) 和角度φ 完全确定，因此，可以用方向向量oβ 和旋转矩阵表示其状态：

根据式（2）易得：

则t 时刻Odom 坐标系下的位置βo(t)可以由（t-1）时刻位置oβ 加t 时刻的得到，通过式（2）逆矩阵变换得：

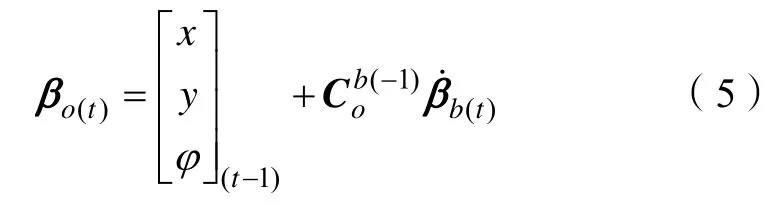
本文所使用移动机器人为四轮驱动结构。前轮舵机控制转向，后轮电机控制速度，所以其运动由后轮线速度速度v 和舵机转向角速度ω 控制。则：

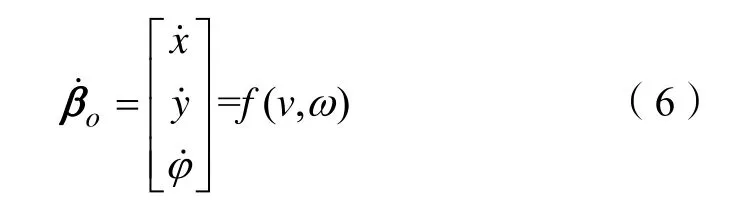
易得：

由上所述，定义移动机器人的状态变量

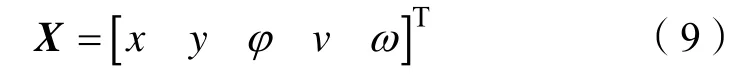
将机器人线加速度及角加速度作为噪声处理，移动机器人运动学模型可以表述为：

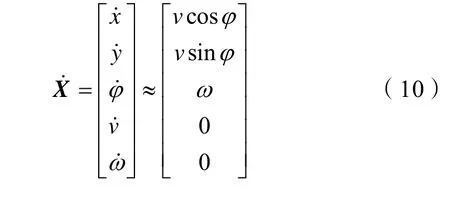
4 传感器观测模型

本文传感器为激光雷达和IMU，通过建立观测模型描述传感器实际测量信号与系统状态变量的联系。

4.1 激光雷达观测模型

移动机器人上配有激光雷达，由于安装问题，激光雷达和移动机器人中心有一定距离，需要通过一次静态TF 变换将激光雷达变换至移动机器人中心。如图2 所示，其中Base_laser 为雷达坐标系，雷达坐标系与机器人本体坐标系Base_link 在Z 轴高度差为12.35 cm，X 轴差7.14 cm。

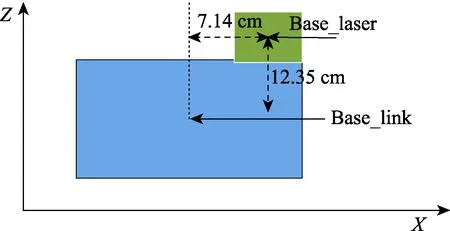
图2 TF 变换示意图

激光雷达通过扫描周围环境获取到点云数据，通过RF2O 方法对点云数据进行处理，获得移动机器人位姿数据，其观测模型为：

对应观测矩阵的雅克比矩阵为：

则RF2O 的观测方程为：

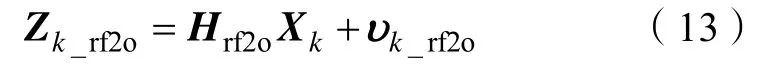
其中：υk_rf2o为RF2O 方法观测噪声，υk_rf2o为高斯白噪声，υk_rf2o～ N(0, Rk_rf2o)。

4.2 IMU 观测模型

对于二维平面运行的机器人，陀螺仪只用测量Z轴的角速度，其观测模型为

本文中对IMU 测得Z 轴的角速度积分得到移动机器人偏航角φ。

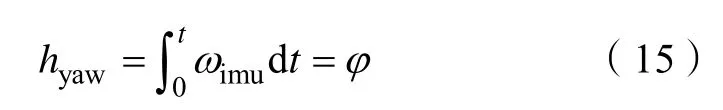
同时对Y 轴方向加速度计测得加速度微分得到速度：

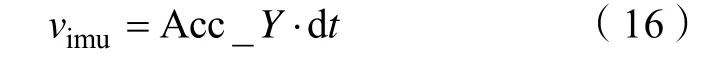
对其积分得到：

由此得IMU 观测模型为：

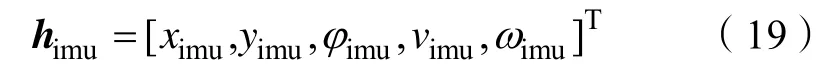
本文将（t-1）时刻 himu值与t 时刻 himu值差分，得到 φΔ、 Δv 作为系统控制输入量。

5 扩展卡尔曼滤波器设计

扩展卡尔曼滤波是一种使用的系统动态模型和一系列随时间变化的观测模型，包含统计噪声和其他不确定性，用来产生估计未知变量的算法[12]。其作用对象是一个非线性控制系统，由于移动机器人的运动学模型存在非线性情况，所以本文采用EKF 融合RF2O数据和IMU 数据。如图3 所示。

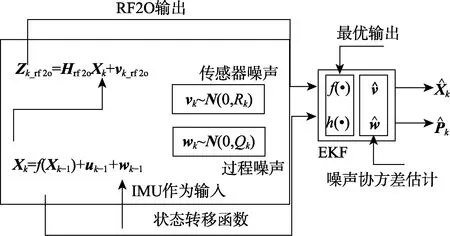
图3 卡尔曼滤波框图

5.1 系统模型及观测方程

移动机器人状态方程为：

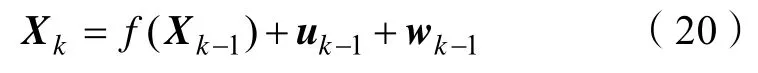
其中：f为非线性系统模型，则f(Xk-1)为移动机器人（k-1）时刻的状态值，uk1-表示（k-1）时刻机器人控制输入。由式（19）差分：

其中wk1-为系统动态噪声，为高斯白噪声。其协方差矩阵为：

将（9）式运用于EKF 时，对其进行离散化非线性处理，以采样周期 Δt 对系统模型离散化，其结果如下：

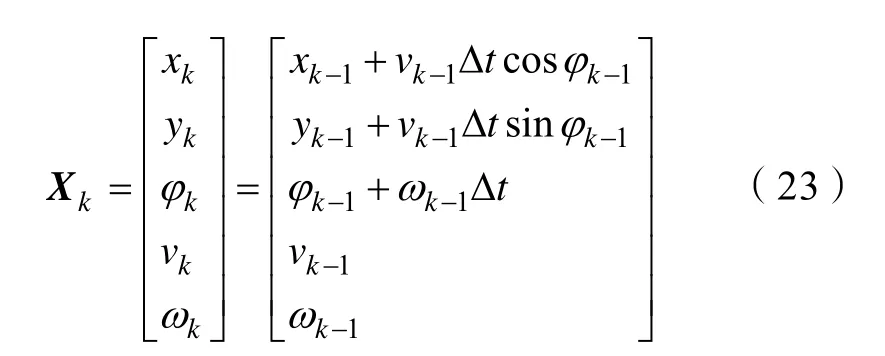
由于系统是非线性的，对函数f 线性化处理，得到雅克比矩阵：

则将状态转移函数一阶泰勒展开得到的雅可比矩阵Fk带入系统方程得，线性化后的系统状态方程为：

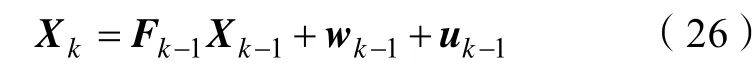
由上述公式，根据卡尔曼滤波基本方程可得，滤波器的预测过程为：

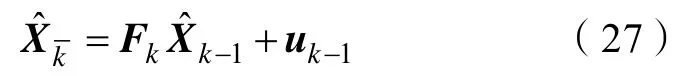
5.2 扩展卡尔曼滤波器更新过程

k 时刻卡尔曼增益矩阵 Kk更新：

k 时刻后验估计值更新：

k 时刻后验估计协方差更新：

6 实验测试与分析

6.1 实验平台设计

本文使用工控机作为主控制器，K-60 单片机作为下级驱动控制器，路由器为主机与从机提供信息交换。机器人实物如图4 所示。

工控机搭载I3-7100U 处理器，4 G 内存，供电12 V，操作系统为Ubuntu16.04+ROS KINETIC。其主要作用是处理激光雷达和IMU 数据并将数据发送给单片机。K-60 单片机接收到工控机消息后输出PWM信号控制舵机和电调驱动移动机器人运行。系统框架如图5 所示。

图4 机器人实物

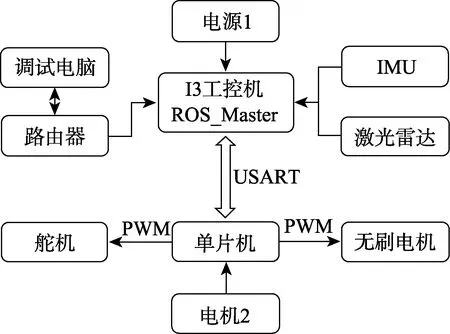
图5 移动机器人系统框图

实验过程如下：

（1）使用键盘控制机器人沿着Odom 坐标系y 方向走2 m，重复10 次。

（2）使机器人绕走廊通过Gmapping 建图并进行路径规划。

6.2 实验结果及分析

实验结果如图6—10 所示，为验证本文融合IMU数据后的位姿估计算法性能，与传统RF2O 方法的误差情况比较，在进行实验步骤1 的实验后，选取其中4 次行走轨迹下的均方根误差分析，其评价函数为

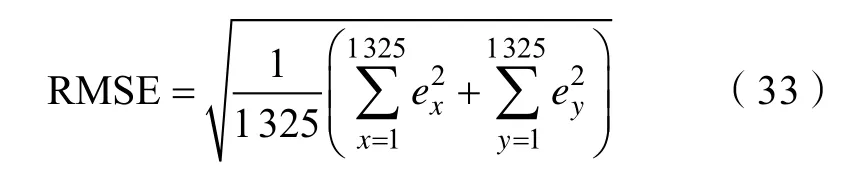
图6 EKF 数据

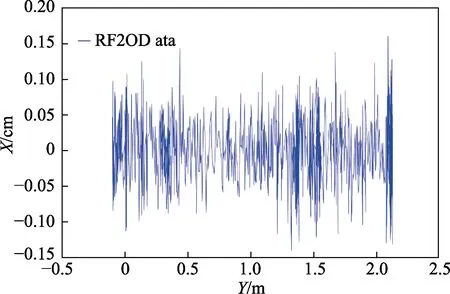
图7 RF2O 数据

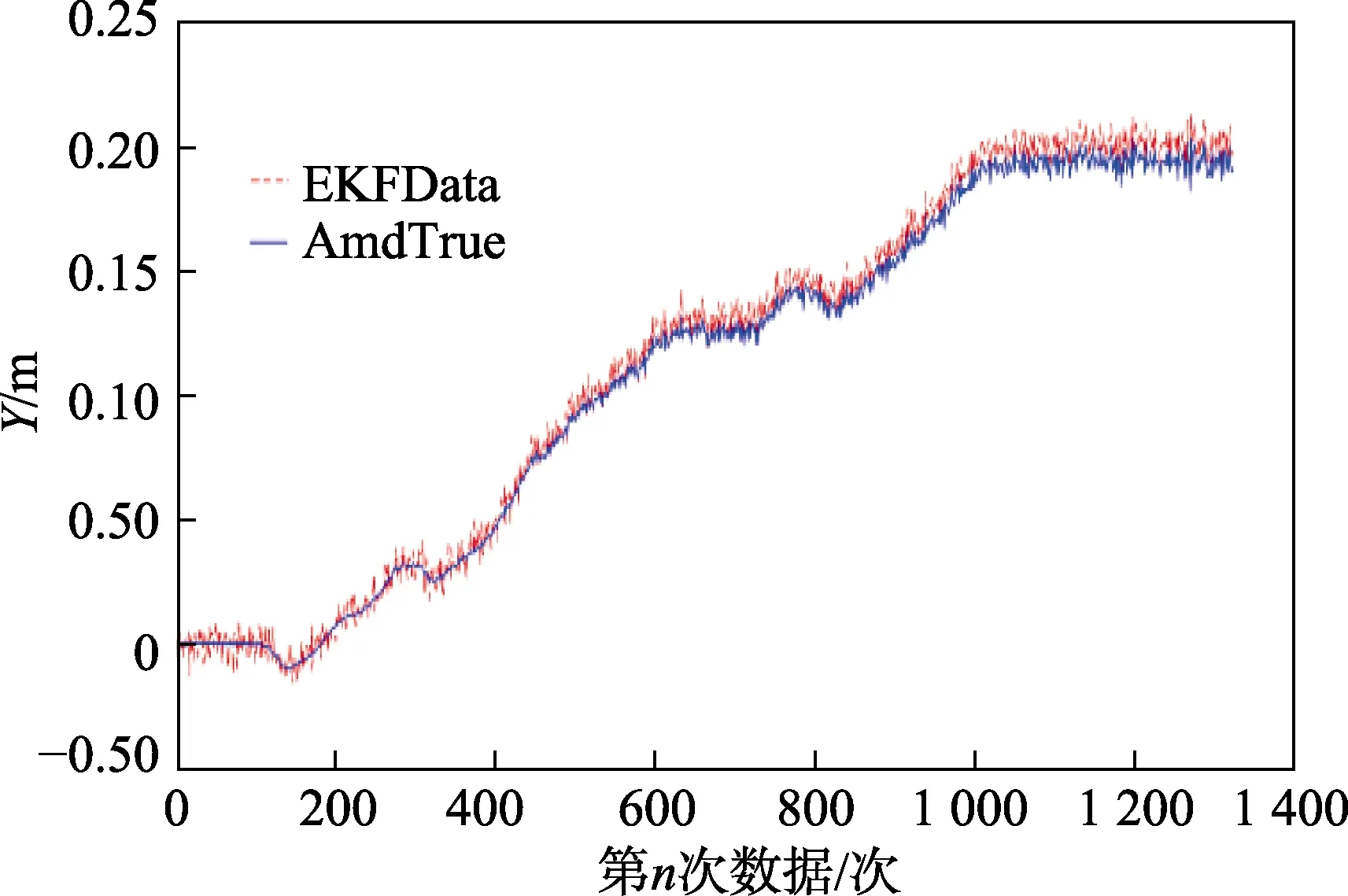
图8 EKF 位姿与真实位姿误差

图9 RF2O 方法与真实位姿误差

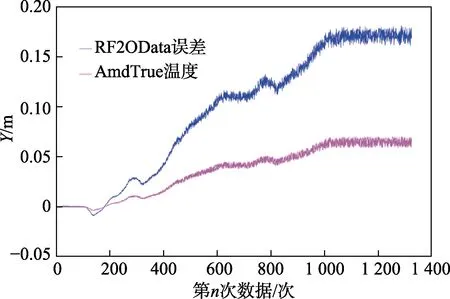
图10 EKF 与RF2O 方法误差对比

表2 均方根误差

可以明显看出，在融合IMU 数据后，RF2O 算法的误差约为融合前误差的76.1%，下降23.9%，效果明显。

使用本文算法所的里程计进行Gmapping 建图效果如图11 所示，所得地图边缘清楚，收敛性好同时距离估计准确。

图11 Gmapping 建图效果

7 结论

通过扩展卡尔曼滤波融合IMU 所得姿态信息与RF2O 所得数据。经过多组实地实验。结果表明：该方法显著降低了由于激光雷达旋转造成的RF2O 方法的累积误差，均方根误差降低23.9%。实现了室内复杂环境下移动机器人的准确定位，该方法不借助编码器等传感器，对于轮胎打滑等造成累积误差的情况能有效避免，在移动机器人室内位姿估计的算法中，具有很大的优越性和实用价值。