中美抗震规范地震记录选取比较

徐朝阳，温瑞智，任叶飞，冀 昆，王宏伟，徐培彬

(1.中国地震局工程力学研究所，哈尔滨 150080； 2.地震工程与工程振动重点实验室(中国地震局工程力学研究所)，哈尔滨 150080)

随着中国强震动记录的积累和结构弹塑性时程分析的普及，相关工程设计人员对强震动记录的选取工作逐渐重视.虽然面向抗震规范的地震动记录选取基本思路与流程是基本一致的，即记录初选、确定目标谱及记录放缩与匹配3个基本步骤，但不同国家抗震规范中的记录选取方案之间存在较大差异[1].中国GB 50011—2010建筑抗震设计规范[2](以下简称中国规范)仅明确规定了加速度时程的最大值，而初选条件、匹配周期等并没有明确规定.作为初选条件的地震动影响参数范围(震级和距离)在中国规范规定相对模糊，国内学者从不同角度提出了地震动记录的选取方案，例如冀昆等[3]提出的地震动全周期匹配法、杨浦等[4]提出的局部周期段匹配法以及陈波等[5]研究的双频段周期匹配法等.除匹配方法外，李爽等[6]和吕大刚等[7]认为目标谱的谱形也会对记录的选取结果产生较大影响.

美国建筑与其他结构的最小设计荷载和相关标准ASCE/SEI 7-16[8](以下简称美国规范)相较于中国规范，甚至美国之前的ASCE/SEI 7-10版本规范都做了全面修订，包括更多的记录选取数量，新的双向反应谱输入方案，更完备的近场地震动选择依据等.和美国规范相比，中国规范并没有明确对记录初选条件，即地震动影响参数范围(震级和距离)明确规定，目标谱匹配周期也较为宽松，采用平均反应谱与目标谱相对误差来判断选波结果，并没有定义下限值.对于三维地震动输入方面的规定也仅有幅值比例要求.

针对以上差异，为了系统性地对国内外抗震规范下的记录选取方法进行对比，本文通过目标谱转换，在同一设防水准下分别按照两国规范的方法进行地震动记录选取，并分别输入到4层和12层框架结构中进行对比.

1 结构模型参数

本文计算所依据的结构为不同层数的两个三维混凝土框架模型，依据中国规范的设防烈度设计配筋.模型1为4层框架结构，层高均为3.6 m，x方向跨度为8 m，共5跨，y方向跨度为6 m，共3跨，采用C30混凝土，钢筋采用HPB300和HRB335；模型2为12层框架结构，1层为5.7 m，2层为4.2 m，其余均为3.3 m，x、y方向跨度均为8 m，共5跨，采用C40混凝土，钢筋采用HRB335，表1给出了相关结构参数，两个框架结构的一阶自振周期分别为0.61 s和1.96 s.

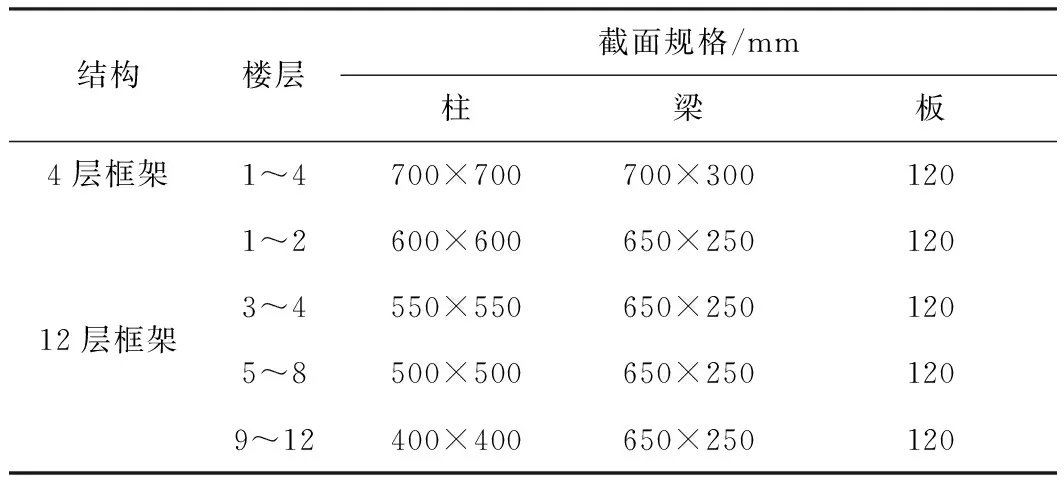
表1 结构模型构件截面尺寸参数

2 中国抗震规范地震动记录选取

2.1 记录初选与调幅

本文随机选用了两种工况：罕遇地震设防烈度7度(0.15g)、场地类别Ⅱ类、设计地震分组第二组(工况1)，和罕遇地震设防烈度8度(0.20g)、场地类别Ⅰ1类、设计地震分组第三组(工况2)，进行地震动记录的选取.

记录选取前首先对地震动和场地参数范围进行初选，冀昆等[9-10]依据不同的震级、震中距范围和场地条件确定了初选条件.但为保证足够的初选记录数量，初选震级Mw定为5.5～8级，场地条件由VS30的范围确定，从美国太平洋地震研究中心(PEER)数据库中初选了330条记录.本节采用保持反应谱谱形不变的线性调幅，调幅目标谱是规范设计谱，调幅系数是由满足规范目标峰值加速度APG的条件下确定.

2.2 反应谱匹配

中国规范在记录选取时，满足“多组时程波的平均地震影响系数曲线与振型分解反应谱法所用的地震影响系数曲线相比，在对应于结构主要振型的周期点上相差不大于20%”的条件.目前国内关于地震动记录匹配的方法有很多，本节采用优化权重最小二乘匹配方法，该方法是全周期最小二乘法的优化，改进了全周期匹配表现差周期段的缺点，用此方法的优势是同种工况可采用同一组选波结果，大大减小了工作量.虽然中国规范要求了中国对于水平两个方向地震动记录幅值比例为1∶0.85，但是本文没有事后对其进行专门的幅值调整，而是尊重了地震动的本来特性，选取时仅对记录的某个水平方向分量进行匹配，另一个分量采用与该分量相同的调幅系数[11].最后选出5条天然地震动记录，而2条人造地震动由Seismomatch软件完成，地震信息见表2.选出的7条地震动反应谱及其均值谱与目标谱比值见图1.由图1可知，选出的地震动在结构主要振型周期点上满足与目标谱相差20%的条件，且谱形与目标谱相似.

3 美国抗震规范中地震动记录选取

由于中美规范在地震动参数的定义上有较大差异，导致二者无法直接对比分析.因此在进行基于美国抗震规范的记录选取工作之前，首先应先进行中美目标谱的地震动参数转换.

3.1 地震动参数转换

中国规范采用了三设防水准，即多遇地震、设防地震和罕遇地震，其50 a超越概率分别对应63.2%、10%和2%～3%；而美国规范仅仅采用了单设防水准，即基于目标风险的最大考虑地震(MCER)，其50 a超越概率为2%，因此张桂铭等[12]和吴桂芳[13]认为MCER与罕遇地震位于同一设防水准.而本文为保证地震动参数的准确对应，参照罗开海等[14]的思路，将罕遇地震分为4个等级，即50 a超越概率分别为3%、2.67%、2.33%和2%，分别对应中国烈度的6度区、7度区、8度区和9度区中的罕遇地震，中国规范给出的50 a超越概率地面运动峰值加速度见表3.

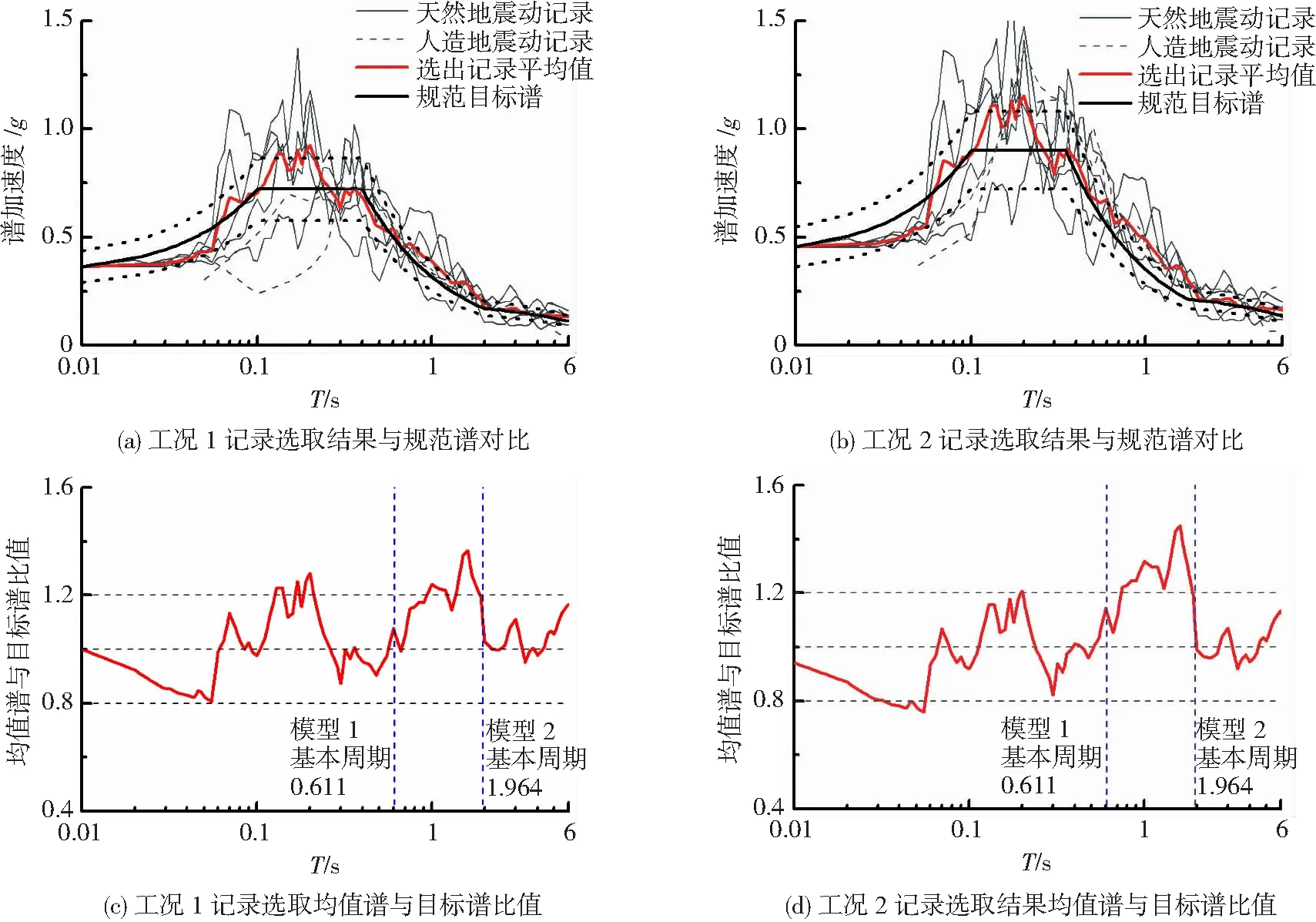
图1 中国规范方法选出的地震动及其均值谱与目标谱比值

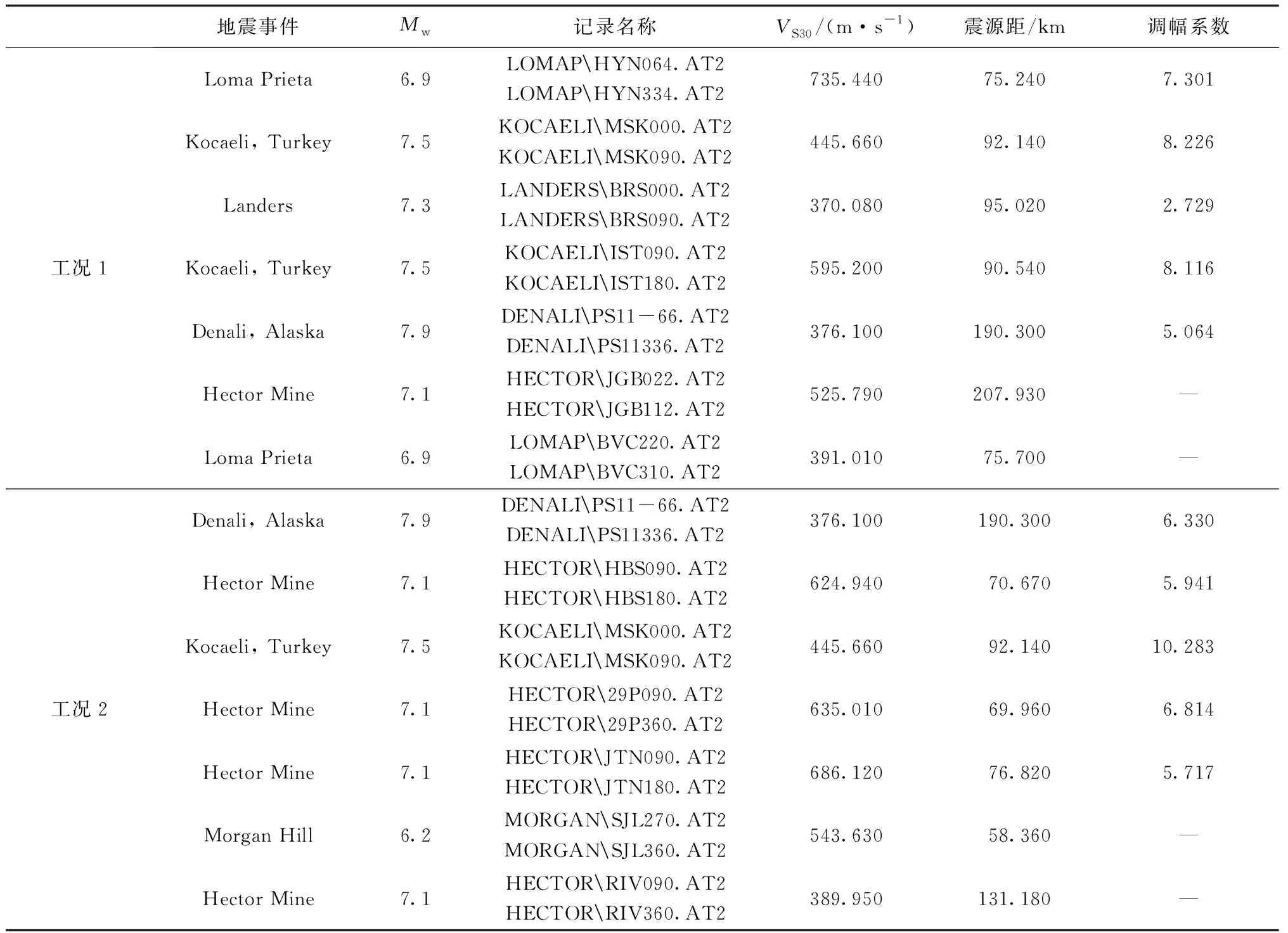
表2 中国规范选出的地震动信息

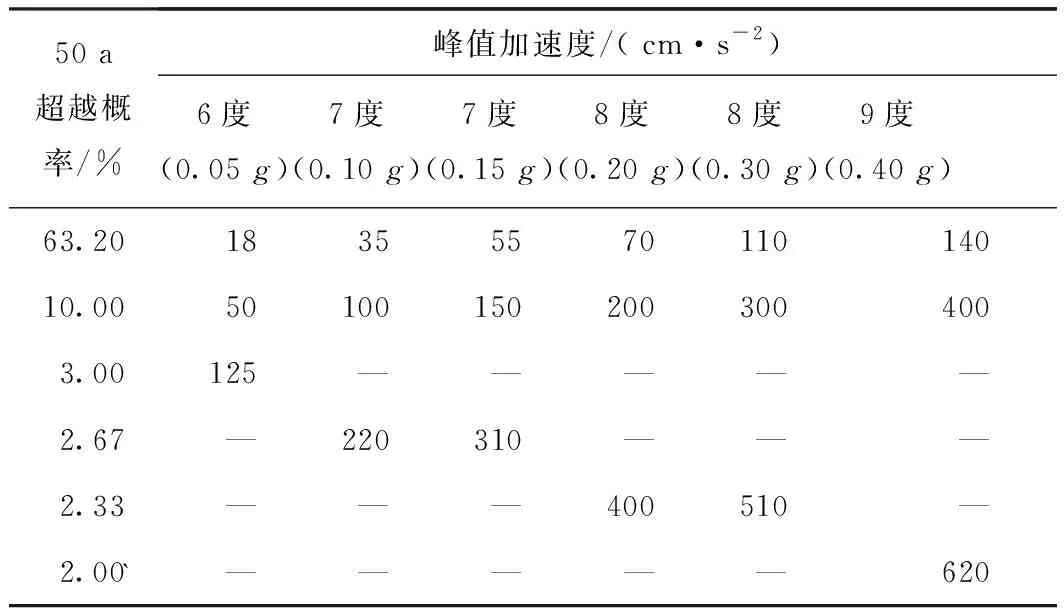
表3 GB 50011—2010规定的地震地面运动峰值加速度

在场地分类上，中国规范按照土层等效剪切波速和场地覆盖层厚度，将建筑的场地类别分为五类(其中Ⅰ类分为Ⅰ0和Ⅰ1两个亚类)；而美国规范仅仅依赖VS30对场地进行分类.Lü等[15]比较了中美场地分类方法，利用VS20与VS30的转换，将中国规范的五类场地与美国的五类场地进行对照.陶林惠等[16]更详细的将场地分类列成表格.本文将延用以上学者的场地分类对照，对地震动记录进行选取.

根据中国规范规定的基本地震烈度和地震分组，按照罗开海等[14]的参数转换思路，将美国规范的地震动参数由式(1)、(2)确定：

SS=2.5γCNACC/Fa,

(1)

S1=2.5γCNTgACC/Fv.

(2)

式中：SS、S1分别为最大考虑地震下(MCER)，B类场地短周期和1 s周期的谱加速度，Fa和Fv分别为与中国规范Ⅱ类场地相对应的某类场地的调整系数，ACC为中国规范与基本烈度相对应的基本地面运动峰值加速度，Tg为中国规范与地震分组相对应的特征周期，γCN为重现期调整系数.

中国规范依据震级和震中距划分了3个地震分组，为充分考虑此方面的不同，在进行地震动参数转换时，应依据中国规范不同烈度分区、不同场地、不同地震分组分别进行计算，最终求得美国规范对应的地震动参数值，表4列出本文两种工况的地震动转换参数.

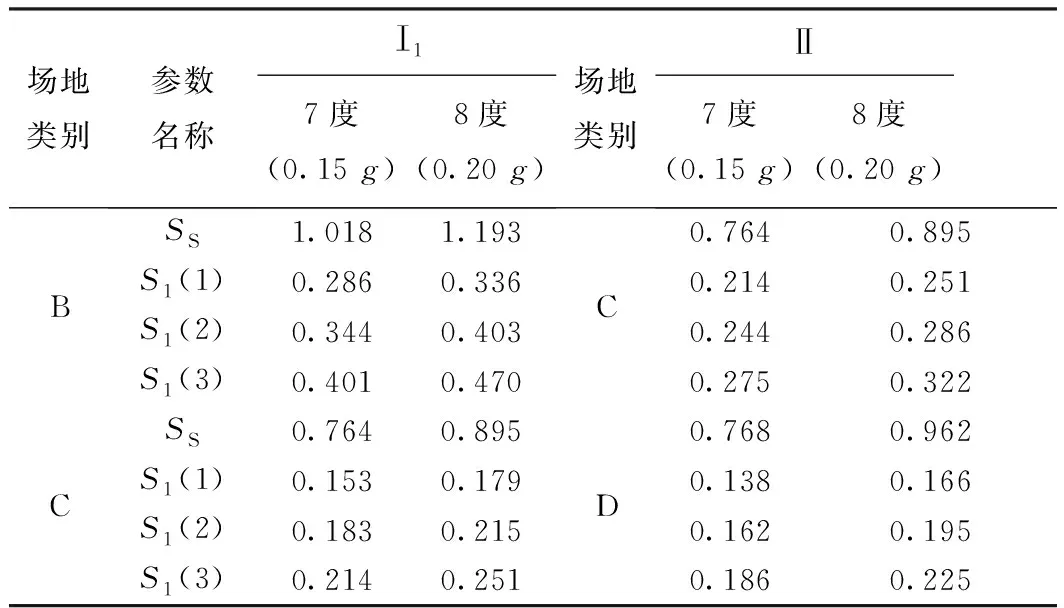
表4 中美地震动参数转换表

因此针对本文中的两种工况，分别将中国规范的参数转换为美国规范的参数，其中工况1将场地对应于C类，工况2也将场地对应于C类.图2给出了两种工况下中美规范谱的对比，可见同种工况下，中国规范的规范谱要大于美国规范的规范谱.对于记录选取依据的目标谱，美国规范规定地震动记录选取时，目标谱值为规范设计谱值的1.5倍，经对比，在本文两种工况下，美国规范的目标谱在0.5 s到2.0 s周期段基本与中国规范目标谱一致.这也是本文所选取框架结构的自振周期所在范围.

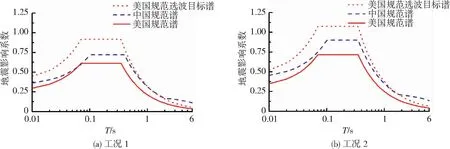
图2 中美规范谱对比

3.2 记录调幅与匹配

不同于中国规范，美国规范的初选条件更加明确，为保证选取结果的可对比性，本文选用与中国规范相同的初选记录库，同时选用与中国规范相同的线性调幅.在调幅时对地震动记录的最大方向谱进行放缩，而不是某一观测方向的记录，其中最大方向谱为Boore等[17]提出的与观测仪器布设方向无关的用来表征两正交水平向地震动的100分位数强度指标，其值参照式(3)，即两正交水平向的强震动记录时程在0°至180°范围内每旋转θ角度后，计算相应的反应谱值，并对不同周期Ti的不同θ条件下对应的值取100分位数.

ACCROT(t,θ)=ACC1(t,θ)×cos(θ)+

ACC2(t,θ)×sin(t,θ),

(3)

式中：ACCROT为旋转后的加速度时程，ACC1和ACC2分别为两观测方向的加速度时程，θ为旋转角度，t为时刻.

美国规范规定经过放缩后的地震动，其最大方向谱的均值在目标周期内不小于90%.其中目标周期段为0.2T和TMIN中的较小值到2.0T之间，其中TMIN表示质量参与系数为90%时的周期，T表示结构基本周期.两框架结构的目标周期分别为0.12～1.3 s和0.38～4.0 s.通过最小二乘周期段匹配法，对目标周期段进行误差排序得到天然地震动的选取结果.

对于美国规范人造地震动的生成，同样采用Atik 等[18]提出的RspMatch2010方法，对调幅后的两水平正交分量地震动记录进行修正，使得在目标周期内，人造地震动的最大方向谱平均值不小于目标谱值的110%，并依据要求排除了近断层地震动.虽然美国规范要求选取不少于11条地震动作为结构的输入，且对于天然和人造地震动比例的选择并没有进行严格的规定，但为保证与中国规范对比的一致性，本文依然选取了7条地震动，选取天然记录和人造记录的比例也定为5∶2.最终依据美国规范选出的7条地震动见图3，地震信息见表5.

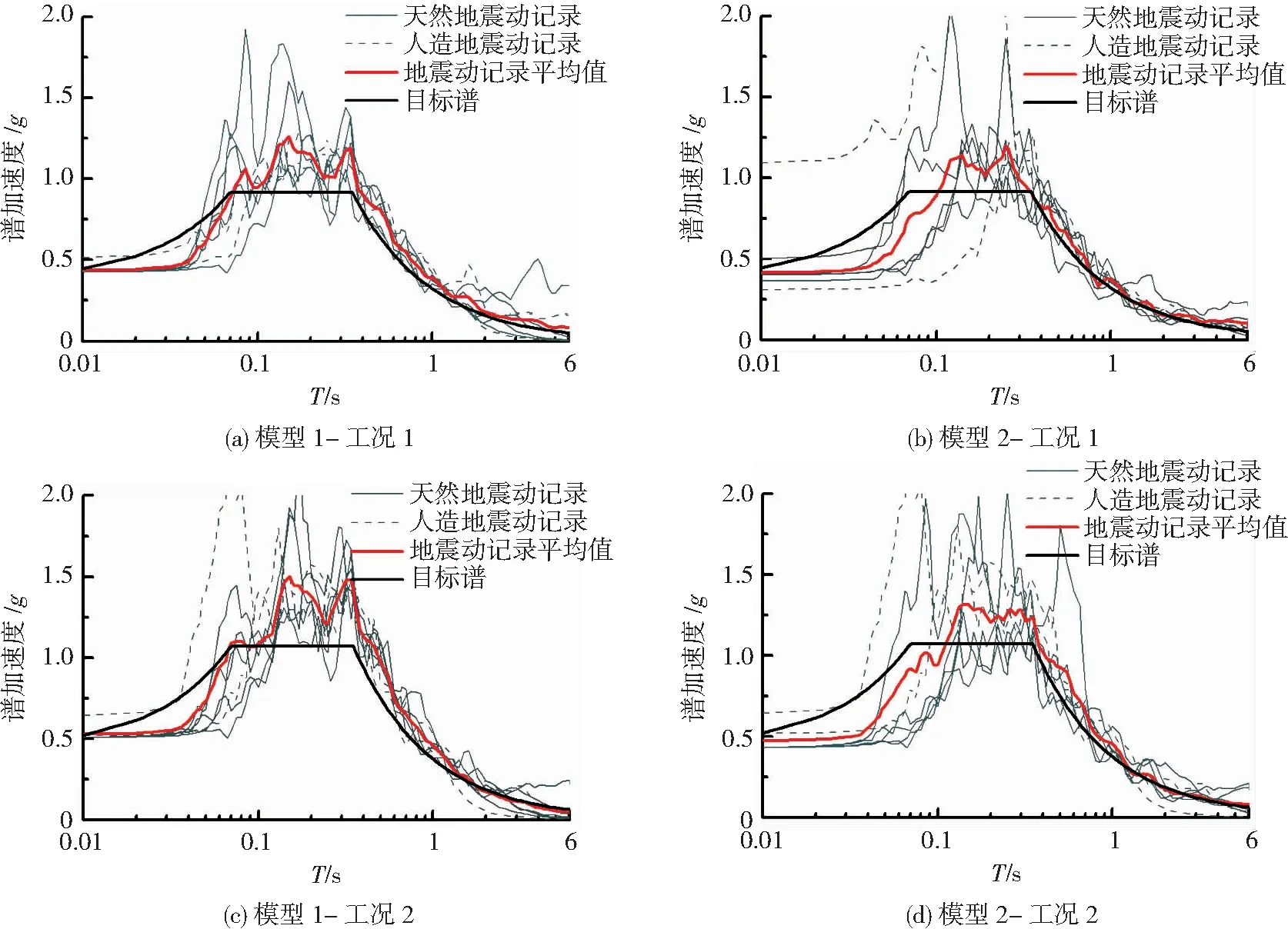
图3 美国规范选出地震动

4 选取结果比较

通过上述步骤，依据中美抗震规范选取工况1、2下适用于模型1和模型2的地震动记录.然后分别将选取结果双向输入到两个结构模型中进行弹塑性时程分析，计算并对比结构的层间位移角和层间剪力.

4.1 中美目标谱下的记录结果对比

本节的相同地震条件指，选用第1节中的两种工况，分别用两种规范下的选波结果作为地震动输入分别对4层和12层框架结构进行双向输入，计算得到两模型在两种工况下的层间位移角和层间剪力，见图4、5.

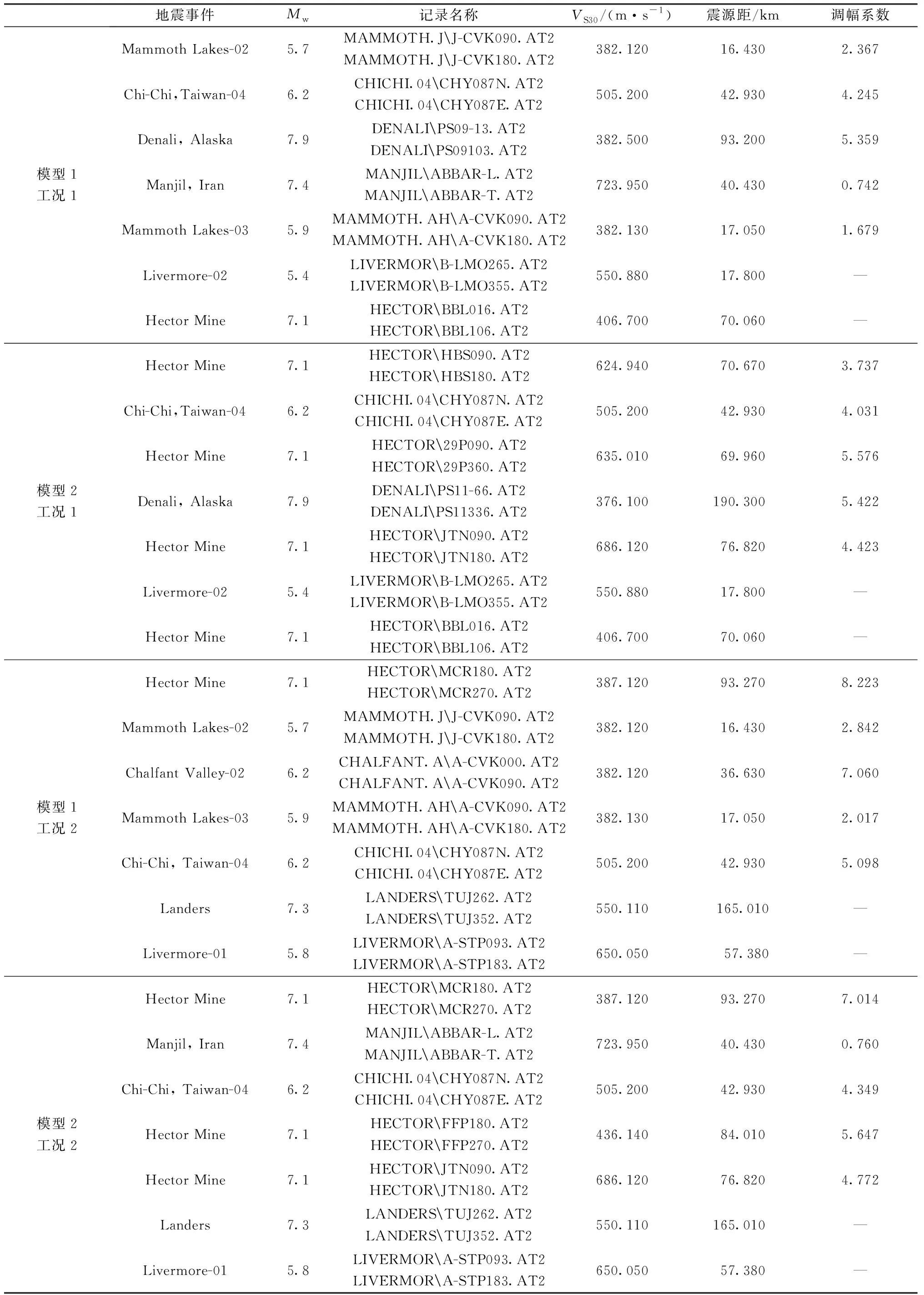
表5 美国规范选出的地震动信息

由对比结果可知，在两种工况下，模型1采用美国规范选取记录得到的层间位移角和层间剪力的平均值和标准差均大于中国规范.作为受一阶振型控制的模型1，虽然中美规范在一阶周期处的目标反应谱值差别不大，但是从图3的记录选取结果来看，美国规范目标谱选波结果的平均反应谱结果均高于目标谱，这主要是由于选波时中国规范仅规定了记录反应谱的相对误差，而美国规范规定了下限，在实际记录选取操作中一般要保证最后平均谱的结果不低于目标谱，这种做法避免了结果的保守，但是可能导致选出的一条或几条记录与目标谱差距过大，这也是造成最后结果存在离散性差异的原因.模型2由于并不单纯受自振周期控制，因此得到的中、美规范下的层间位移角和底部剪力平均值之间没有明显的大小规律.由于中国规范选波时只考虑了某个方向的反应谱匹配(即本文的x方向)，未考虑y方向，从而导致y方向的中国规范记录选取结果可能会离散性较大，如模型2-工况1所示.

4.2 中美匹配方法下的记录结果对比

由于目标谱对选波结果的影响较大，因此为排除不同目标谱的结果差异性，现将两种方法目标谱统一，即均采用中国规范目标谱，分别按2、3节的方法选取地震动，再次比较两种方法的计算结果，见图6、7.

图6和7中表明，当二者统一目标谱后，模型1中的层间位移角和底部剪力的平均值基本相同，目标谱不同导致的结果差异性消失；而美国规范的标准差依然大于中国.模型2中除工况2的y方向，美国规范的层间位移角和底部剪力的平均值依然小于中国，说明美国规范选出的记录与目标谱匹配度高于中国；x方向中国规范的标准差小于美国，y方向中国的标准差大于美国，这与中国规范选波时只考虑x方向有关，美国规范的标准差在两个方向上差异较小.

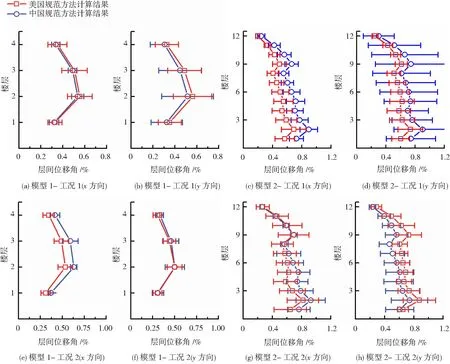
图6 中美匹配方法下层间位移角计算结果对比

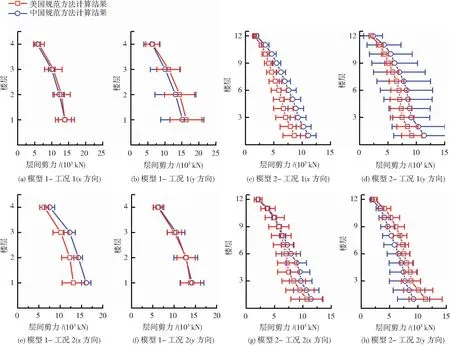
图7 中美匹配方法下底部剪力计算结果对比

5 结 论

本文分别按照中国规范和美国规范进行地震动选取，以4层和12层框架结构为算例，对比了二者方法的表现，得到如下结论：

1)中国抗震规范在地震动记录选取时没有明确可操作的双向地震动选取方案，如基于单一方向选取和调幅，可能导致另一方向的地震动与目标谱匹配度不高，使得计算结果离散度偏大.美国抗震规范采用最大方向谱选取，虽然计算复杂，但是具有更明确的物理意义，可以较好体现记录不同合成方向的最大谱响应.

2)记录选取时中国规范仅规定了记录反应谱的相对误差，而美国规范规定了下限，在实际记录选取操作中一般要保证最后平均谱的结果不低于目标谱，这种做法虽然避免了结果的保守，但是可能导致选出一条或几条记录与目标谱差距过大，这也是造成最后结果存在离散性差异的原因.

建议结合二者的优点，在控制相对误差的同时，也引入下限限制的遴选机制.