基于栈式自编码器的土质边坡失稳风险评估

于 锦，谭 飞，仝德富，郭永楠，马邦闯

(中国地质大学工程学院(武汉)，湖北 武汉 430074)

边坡失稳产生的滑坡灾害同地震灾害、火山灾害一样已经成为影响人类生存和发展的三大地质灾害之一。我国每年由于各种滑坡造成的经济损失高达200亿元[1]。因此，开展边坡风险管理，有效地判断出边坡的风险等级，指导边坡的施工，并降低施工风险，确保生产安全具有重大的意义。

在边坡失稳风险评估方面，国内外学者进行了大量的研究。如Li等[2]基于有限元与可靠度理论确定了边坡最危险滑裂面和滑动体体积，据此定量分析了边坡风险的影响因素和损失；Xiao等[3]提出了一种辅助随机有限元法，在考虑土体性质空间变异性的情况下，可有效地对三维边坡进行可靠性分析和风险评估；Zhang等[4]基于层次分析法和模糊识别理论建立了膨胀土边坡失稳风险分析模型；Ferrero等[5]基于精确的地质结构调查，评估了边坡稳定性条件；Pinheiro等[6]通过对影响边坡的9个参数分配权重计算得到边坡质量系数，并根据经验划定边坡质量系数等级，进而评估边坡失稳风险；Macciotta等[7]定量化计算了边坡失效的风险，力求最小化边坡失效风险评估过程中的不确定性因素；Mori等[8]基于地形数据，提出了一种在暴雨工况下边坡失稳风险评估模型；李东升[9]将可靠度理论与风险评估结合，以决策树作为分析工具，在考虑边坡工程投资和相应风险的基础上，进行边坡工程风险决策，在一定程度上消除了决策过程中人为因素的影响，使决策更具科学性；张雷等[10]在分析高等级公路边坡工程风险因子的基础上，应用层次分析法对边坡失稳风险等级进行了评估研究；何海鹰等[11]基于层次分析法，利用岩质边坡风险的诸多影响因素建立了岩质高边坡风险评估指标体系；梁涛等[12]基于模糊层次分析法原理、步骤和MATLAB语言环境，通过需求分析、界面设计、代码编写、功能模块设计等流程，研发出公路边坡风险评估软件RASlope；李典庆等[13]基于子集模拟的边坡风险评估的高效随机有限元法，推导出基于子集模拟的边坡失效概率和失效风险的计算公式。

上述研究中，大多采用模糊集理论、层次分析法、有限元理论等建立了边坡失稳风险评估模型，或是采用概率论方法计算边坡失效概率并确定边坡失稳风险等级，或是考虑一些特殊工况下边坡风险的影响因素，而在确定边坡风险影响因素的权重值或概率时，通常采用专家打分法、头脑风暴法、事故树分析法、频率统计法等方法，其中一些方法存在许多人为主观因素的影响，且计算权重的过程也较为繁琐。

深度学习源自于机器学习，是一门人工智能科学。机器学习发展至今，最重要的网络模型即人工神经网络模型。深度学习是人工神经网络的进一步深入，也称为深度神经网络，它较普通BP神经网络具有更深的结构层次、更多的激活函数种类、更多的模型结构、更加智能等特点，主要包括卷积神经网络[14]、深度信念网络[15]、循环神经网络[16]、自编码器神经网络[17]等。其中，自编码器神经网络能降低数据维度，获取最优初始参数，是一种无监督学习的神经网络，它可以不断地调整参数以重构经过压缩的输入样本。而栈式自编码器是自编码器的一种多层组合，当维度压缩到合适的状态、参数足够优化时，将多个自编码器连接可得到栈式自编码器。本文基于深度学习模型——栈式自编码器开展了土质边坡失稳风险评估研究，可快速评估土质边坡失稳风险，并克服了传统方法计算量大、处理过程复杂等缺陷，以提高边坡风险管理效率。

1 土质边坡稳定性影响因素的确定

影响土质边坡稳定性的因素较多，一般基于最主要的控制性因素开展土质边坡稳定性研究。如夏元友等[18]以土体容重、黏聚力、内摩擦角、边坡角、边坡高度、孔隙水压力(孔隙水压力系数)6个主要因素为研究对象，应用RBF神经网络开展了土质边坡稳定性影响因素的敏感性分析；冯夏庭等[19]同样基于上述6个土体参数，应用BP神经网络开展了土质边坡稳定性评价；高超等[20]以上述6个土体参数中的5个土体参数为研究对象，应用神经网络开展了黄草坝古滑坡稳定性研究。可见，上述6个因素是影响土质边坡稳定性的最主要因素。此外，夏季暴雨时节往往是滑坡灾害发生的高发时期，因此水的影响不可忽视；地震对土质边坡的影响同样巨大，强震之下土体振动液化时有发生；人类生产生活也会加剧滑坡风险。因此，本文基于上述影响土质边坡稳定性的6个主要土体参数以及年均降雨量、抗震烈度、人类活动共9个因素，开展了土质边坡失稳风险评估研究。

在对土质边坡稳定性各影响因素的风险等级进行划分时，应做到合理布局，风险等级划分过多、过于细化，则会使数据处理过程较复杂，模型训练耗时加大，不利于工程应用；若风险等级划分过少、过于简单，则针对性、差异性不强，总风险评级结果则不具参考价值。土质边坡稳定性的风险等级划分后采用类似二进制方式进行标定处理，方便数据在模型中的输入和输出，有利于提高模型的训练效率和预测结果的准确性。本文在详细阅读和分析相关文献[21-25]的基础上，将土质边坡失稳风险分为3级，1～3级边坡失稳风险程度递增(见表1)，并采用类似二进制方式对每个风险等级进行标定，标定值见表1；分别将上述9个影响因素划分为4～5个风险等级，也采用类似二进制方式对各影响因素的每个风险等级进行标定，其标定值见表2。

表1 土质边坡失稳风险的分级与标定

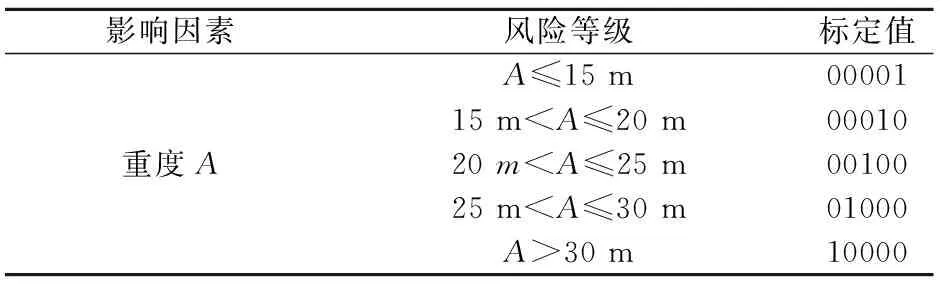
表2 土质边坡稳定性影响因素风险的分级与标定

续表2

2 栈式自编码器网络结构

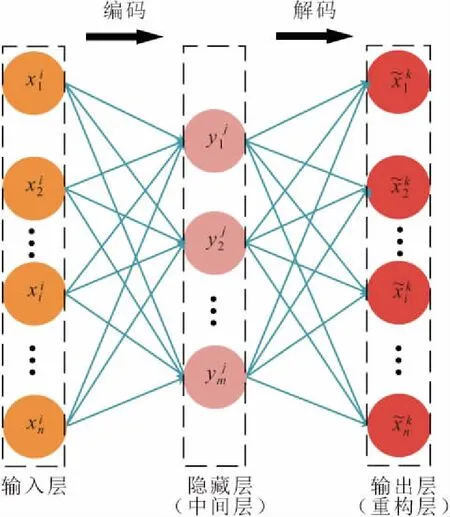
图1 自编码器(三层结构)Fig.1 Autoencoder (three-layer structure)

栈式自编码器由自编码器堆叠构成。自编码器包括编码和解码两个部分，数据先通过输入层进入中间层进行编码，然后压缩成更低维度的数据，从中提取数据特征，最后进入重构层解码还原数据，见图1。经过多组数据训练后，模型可学习到数据的特征及其映射关系。输入数据xi的编码过程如下式：

yj=f[(wij)Txi+bj]

(1)

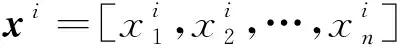
(2)

(3)

f(x)=max(0,x)

(4)

由上述3个函数式可知，Sigmoid函数的值域为[0,1]，Tanh函数的值域为[-1,1]，Relu函数的值域为[0,+∞]。而本文对各影响因素值进行标定后，每个因素都被转换为0、1表示，因此应用Sigmoid函数作为本模型的激活函数是合适且可行的，见图2。

图2 Sigmoid函数Fig.2 Sigmoid function

中间层与重构层之间的解码过程如下式：

(5)

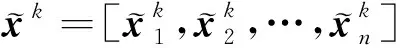
(6)

(7)

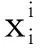
重构层误差项计算公式为

(8)

式中:δk为重构层k上的误差项；zk为重构层的输入值。

中间层误差项计算公式为

(9)

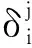
依据上面公式计算得到的误差项需进行连接权值和偏置值的修正。

重构层权值的修正公式为

wjk(n+1)=wjk(n)+η·δk·yj

(10)

式中:η为学习效率；n为权重w被修正的次数。

中间层权值的修正公式为

wjk(n+1)=wij(n)+η·δj·xi

(11)

重构层偏置的修正公式为

bk(n+1)=bk(n)+η·δk

(12)

中间层偏置的修正公式为

bj(n+1)=bj(n)+η·δj

(13)

输入一个样本数据即进行一次上述运算时，则表示完成了一个样本数据的学习。遍历一次训练样本，即完成一次训练。当重构值与输入值之间的误差达到要求精度，停止模型训练，输入测试样本，进行泛化能力测试。

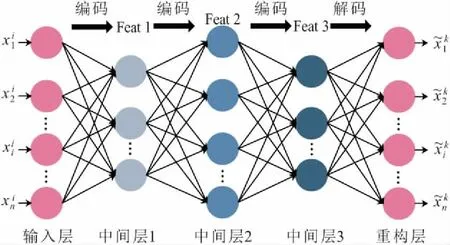
图3 栈式自编码器结构Fig.3 Structure of stacked autoencoder

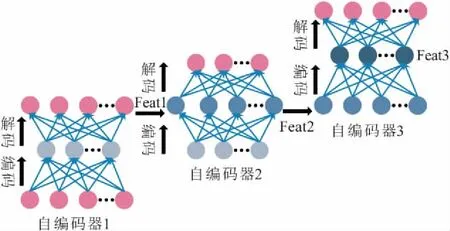
图4 栈式自编码器的训练过程Fig.4 Training process of stacked autoencoder

3 模型构建与训练

本次研究从某高速公路施工便道边坡和湖北秭归县、巴东县等边坡工程收集了44个边坡样本，边坡样本土体以粉质黏土为主，土体容重介于10～24 kN/m2，边坡高度介于1～75 m，边坡角介于20°～75°，黏聚力介于10～25 kPa，内摩擦角介于0°～45°，孔隙水压力系数介于0～1。地震、降雨和人类活动频度依据边坡所在地的实际情况确定。为了避免模型训练过程产生过拟合、精度不高等问题，借鉴深度学习中数据增强(Data Augmentation)的方法将样本集数据增强到156个。数据增强的目的是让有限的数据产生更多的等价数据，增加训练样本的数量和多样性(噪声数据)，提升模型鲁棒性[26]。数据增强方法在图像识别等深度学习模型中应用较为广泛，主要操作方法包括几何变换(旋转、翻转、裁剪、拼接等)、色彩空间变换、随机擦除、对抗训练、神经风格迁移等。通过生成随机数为样本序号，随机划分136个训练样本和20个测试样本，并依据表1和表2对样本数据进行标定处理。

对样本数据标定之后，输入数据维数由9变为39，输出数据维数为3。初步拟定使用一个编码器，样本数据将由39个维度(39个神经元)降低到18个维度(18个神经元)，再经分类层(3个神经元)输出，见图5。自编码器的激活函数采用Sigmoid函数，分类层采用Softmax函数，自编码器单独的无监督训练采用二次代价函数，即以公式(6)为误差函数，分类层训练和栈式自编码器有监督情况下的微调均采用交叉熵代价函数，即以公式(7)为误差函数。自编码器单独训练时，训练误差随迭代次数的变化见图6。

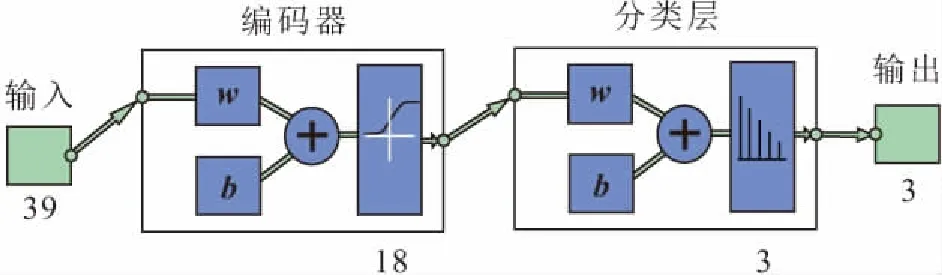
图5 土质边坡失稳风险评估栈式自编码器Fig.5 Stacked autoencoder of instability risk assessment of soil slope

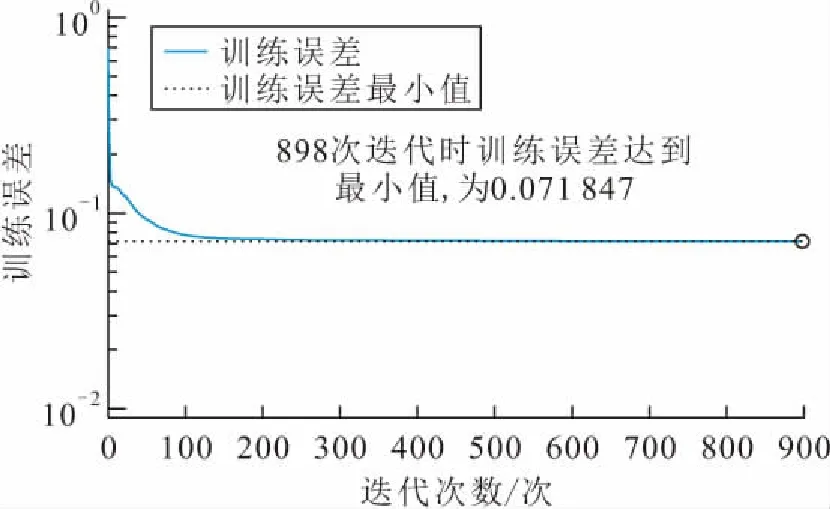
图6 自编码器训练误差随迭代次数的变化Fig.6 Variation of training error of autoencoder with the number of iterations

由图6可见，当自编码器训练到898次时，训练误差最小值约为0.07，可判定此时的精度基本达到要求，可结束训练。

4 模型泛化能力测试

经过训练后，对模型泛化能力进行测试，得到20个测试样本的预测输出值与目标值的对比以及模型泛化能力测试精度的混淆矩阵，见表3和图7。

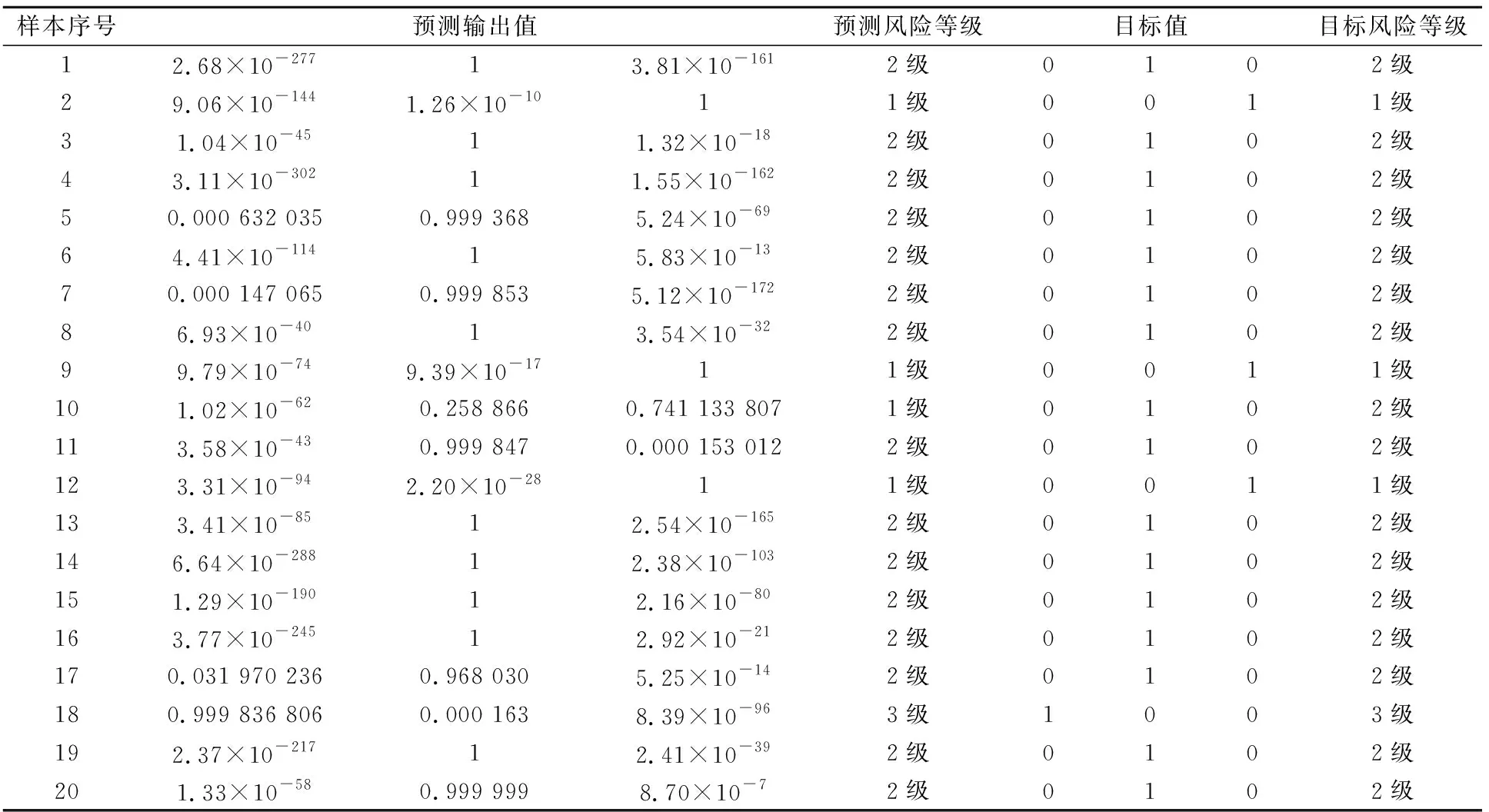
表3 模型泛化能力测试结果

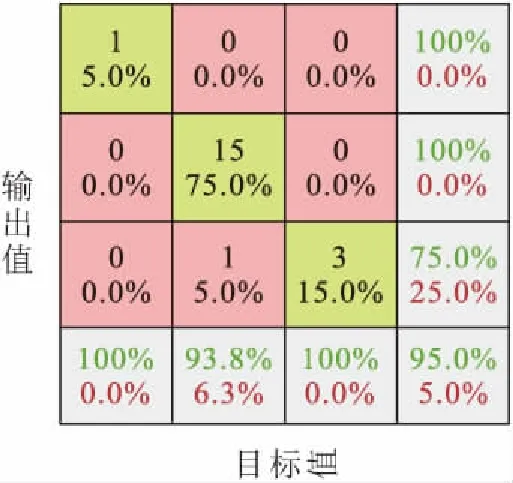
图7 模型泛化能力测试精度的混淆矩阵Fig.7 Confusion matrix of accuracy of generalization ability test accuracy of the model

由表3和图7可见，本文提出的土质边坡失稳风险评估模型，获得了数值上95%的准确率；除10号样本未达到预期值外，其他样本均得到了高精度的预测输出值。由此可见，本文应用栈式自编码器建立的土质边坡失稳风险评估模型是可行且有效的，可将该模型应用于土质边坡工程失稳的风险等级评估。

5 结论与建议

本文基于栈式自编码器深度学习模型，提出了一种快速评估土质边坡失稳风险的方法，主要得到以下结论：

(1) 运用栈式自编码器建立的土质边坡失稳风险评估模型具有计算速度快、评估结果客观性高等特点，并获得了数值上95%的准确率，说明应用深度学习模型构建风险评估模型进行土质边坡失稳风险评估是可行且有效的。

(2) 本文提出的方法仅需依据工程勘察资料，获取边坡稳定性的9个影响因素后，即可快速预测得到边坡失稳的风险等级。由于边坡状态会随着气候、人类活动等外界因素而发生变化，运用本方法可在边坡的不同阶段和不同状态下，多次快速地确定边坡失稳的风险等级，从而为开展边坡全寿命风险管理节约了成本，加快了边坡失稳风险等级评估过程。

(3) 深度学习中有许多模型可以利用，将性能更佳的深度学习模型运用于边坡、隧道、地下空间工程的风险评估、变形预测、超前地质预报等研究，将可获得更多意义重大的研究成果，这也是今后的研究方向。