基于ANSYS的发动机曲轴有限元静力与模态分析
余佳奎 李舜酩 李想 张蒙

摘 要:本文对某V10发动机曲轴进行有限元分析,并运用Solid Works软件构建了曲轴模型,应用ANSYS Workbench软件模拟分析了曲轴在各气缸发火做功时的静态力学性能以及曲轴的振动特性,得出曲轴在模拟工况下的应变、应力分布情况,并得出曲轴的自由振动模态与在约束情况下的振动模态。计算结果表明,曲柄连杆轴颈的过渡圆角与主轴颈的过渡圆角位置是危险区域,最终得到该曲轴的最小固有频率,为该曲轴的可靠性分析、疲劳强度校核提供计算基础。
关键词:曲轴;有限元分析;力学分析;模态分析
中图分类号:U464.13文献标识码:A文章编号:1003-5168(2020)23-0036-06
Abstract: In this paper, a finite element analysis of a V10 engine crankshaft was carried out, and a crankshaft model was constructed by using Solid Works software, and the ANSYS Workbench software was used to simulate and analyze the static mechanical properties of the crankshaft when each cylinder was firing and doing work and the vibration characteristics of the crankshaft, and the strain and stress distribution of the crankshaft under the simulated operating conditions were obtained, and the free vibration mode of the crankshaft and the vibration mode under restraint were obtained. The calculation results show that the transition fillet of the crank connecting rod journal and the transition fillet of the main journal are dangerous areas, finally, the minimum natural frequency of the crankshaft is obtained, which provides a calculation basis for the reliability analysis and fatigue strength check of the crankshaft.
Keywords: crankshaft; finite element analysis; mechanical analysis; modal analysis
曲轴是发动机最主要的部件之一,也是最难加工的部件之一。发动机运转时,气缸内的混合可燃气被点燃,可燃混合气对活塞做膨胀功,迫使发动机活塞上下运动,然后通过活塞接触的连杆带动发动机曲轴,使曲轴做旋转运动。在发动机运行时,气缸内混合可燃气周期性爆发,产生出周期性变化的载荷,该载荷通过活塞连杆施加给发动机曲轴,显然,曲轴在承受弯曲应力和扭转应力下的工作条件极其苛刻,强度与寿命都面临巨大挑战[1];一旦曲轴发生疲劳失效甚至是断裂,会损坏发动机的其他部分,导致安全事故,尤其是在提高发动机性能和可靠性方面,发动机曲轴必须满足强度设计要求后才能安装和运行[2]。
除了强度需要满足设计要求之外,曲轴的振动特性也是在曲轴设计时需要考虑的问题。固有频率指的是当物体受到外部瞬态激励时曲轴响应振动的频率,一个物体往往有许多不同的固有频率,曲轴亦是如此。当上述各种载荷所产生的振动迫使曲轴响应振动时,在激励振动频率与固有频率相近甚至相同时,共振现象将会发生,更可能导致曲轴疲劳失效,甚至在此工作条件下曲轴结构出现破坏[3],如果发生这种情况,会导致安全事故。因此,设计曲轴时,为了避免出現共振现象,必须进行曲轴模态分析,得到曲轴固有频率,只要激励频率超过固有频率的40%,就可以避免共振或在隔振中起作用[4],保证曲轴在发动机运行时的可靠性。
早在19世纪末,就有外国学者考虑曲轴扭转问题,由于技术水平的不足,轴系都是作为绝对刚体处理。伴随着计算机技术的发展和相关计算机分析软件的开发,人们逐渐找到了一些复杂系统扭转振动问题的新解决方案。用有限元方法来进行模态分析,为曲轴的动态分析提供了新方法。Raub等[5]对曲轴进行柔性化处理,结合刚体动力学,对曲轴实行有限元分析,并且对曲轴的振动频率进行追踪,最终获得了与试验数据高度吻合的仿真分析结果。郭磊等[6]对轴系中不同的机构分别采用模态综合技术、雷诺油膜方程,构建了与气缸体耦合的曲轴模型,在通过仿真结果与试验数据的对比之后,验证了耦合系统多体动力学仿真的有效性。有人利用AVL发动机仿真软件设备,对汽车整个传动系进行仿真分析,获得了整个传动系的扭振特性,并且优化了传动系统的扭振频率。当前,曲轴振动的研究大多使用有限元法,除了研究轴系扭转振动特性外,也有研究轴系的三维耦合振动、轴系与机体耦合作用下的振动等[7]。
本文将以曲轴的载荷以及运功轨迹图为基础,分析曲轴在发动机运行时的工作情况,利用Solid Works软件对曲轴建模,并结合ANSYS Workbench进行有限元分析,得出曲轴的应变、应力分布情况,对其强度进行校核,计算出曲轴的振动固有频率。
1 曲轴三维模型建立
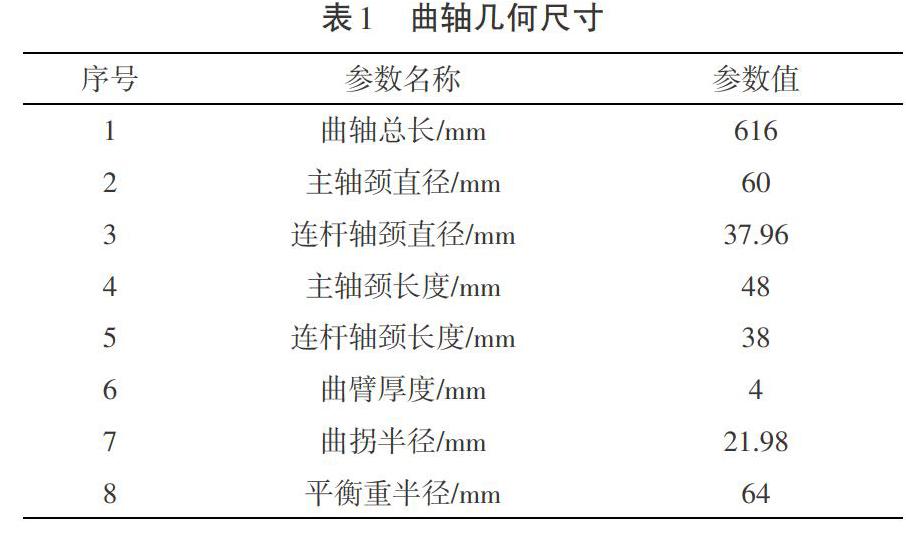
鉴于曲轴的结构并不简单,并且ANSYS自带的三维建模模块的操作也不简单,所以曲轴三维模型采用Solid Works软件完成,曲轴的三维模型如图1所示。曲轴的主要几何尺寸如表1所示。
2 有限元静力学分析
2.1 有限元静力学分析网格划分
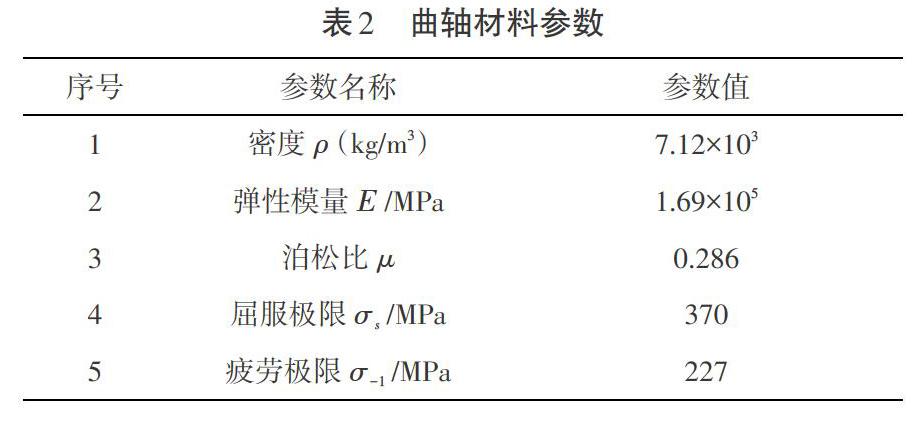
ANSYS软件共有两种构建有限元模型的方法,即直接法和几何模型网格划分法。本文使用的是直接法。创建有限元模型时,首先要定义单元类型、单元实常数、材料属性等参数。对于本文研究的曲轴,其材料选用牌号为QT600-3的球墨铸铁,其属性如表2所示。在ANSYS Workbench的Engineering Date中輸入,密度[ρ]=7.8×10-9 kg/m3,弹性模量[Ε]=1.0×105 MPa,泊松比[μ]=0.23。在本文研究中,体网格设置为2 mm,采用自动划分方法进行网格划分,得出的有限元模型共划分单元63 806个、节点103 413个,如图2所示。
2.2 运动条件加载
发动机曲轴的运动约束条件分别为位移边界约束条件和力边界约束条件。边界条件有连杆对曲轴的推拉作用力、主轴承对曲轴的支撑作用力、飞轮传递的扭矩、曲轴的旋转离心力以及曲轴的重力[8]。
发动机中的活塞、连杆和曲轴是在模拟发动机运行的工况下曲柄连杆机构的位移部件。其中,活塞作往复位移;曲轴绕回转中心旋转;连杆小头与活塞一起做往复位移,连杆大头和曲柄销一起绕回转中心旋转,整个连杆有复杂的平面运动[9]。
本文研究的十缸四冲程发动机的点火顺序为1-6-5-10-2-7-3-8-4-9,如图3所示,图2中右端是曲轴前端。有试验结果表明,在承受最大爆发压力时,曲轴出现最大的载荷和变形情况。曲轴主要损坏原因来自弯曲引起的破坏,可以根据这个缘故进行简化操作,假定活塞处于上止点位置时,对于发火的气缸,连杆轴颈载荷达到最大值[10]。
2.3 位移边界条件
按照发动机结构要求,主轴承不可径向窜动,所以在主轴颈上施加径向约束;因为本次分析是静态力学分析,在后端凸缘端将选中的节点施加全约束,不让曲轴发生旋转,并且防止此端面的轴向、径向移动;在自由端仅限制其径向运动和旋转运动,因为曲轴受力会有轴向伸缩,两端不能都约束轴向运动[11]。
2.4 力边界条件
依照传统方法以及有限宽度轴颈油膜压力分布规律,可以不考虑油孔处压力峰值突起对结果的作用,并可将力边界条件设定(即假定轴承支座反力和连杆轴颈受力遵循以下条件)为:载荷沿连杆轴颈和主轴颈轴线方向按二次抛物线分布,在沿轴颈径向120°范围内按余弦规律分布[11],因此设定曲柄销处的作用力为5 000 N,在飞轮段施加曲轴所受的扭矩为5 000 N·m。
2.5 计算结果与分析
选择第一气缸爆发时,即第一气缸发火状况下活塞处于压缩行程终了时,分析曲轴受力情况。加载情况如图4所示。
由理论分析预测,当第一气缸发火时,第一连杆轴颈与主轴颈相连圆角部位是应力最大的部位。经ANSYS Workbench计算,得到如下结果。图5为第一气缸发火时曲轴整体的应变云图,图6为第一气缸发火时曲轴整体的应力云图。
从曲轴整体应力应变图可以看到,当第一气缸发火时,应力最大的位置是临近第一连杆轴颈的主轴颈过渡圆角位置,最大应力值为50.419 MPa,另外存在应力比较大的位置,比如,另一侧主轴颈过渡圆角位置最大应力值介于20~40 MPa。变形最大的地方是第一连杆轴颈与曲柄连接圆角处,最大应变值为0.013 033 mm。
按同样方法分别计算得出各缸发火时的曲轴整体应力、应变云图,由于篇幅原因,本文只展示最大应力值时的应力、应变云图。将各缸发火时曲轴出现的最大应力值汇总,计算结果如表3所示。
从表3可以看出,最大应力值产生在第一气缸发火时,应力值为50.419 MPa,最小应力值产生在第三气缸发火时,应力值为23.221 MPa。
该曲轴材料的屈服极限[σs][]=370 MPa大于模拟工况下的最大应力值50.419 MPa,所以该曲轴满足结构的刚度要求。
另外,曲轴的循环弯曲疲劳极限为227 MPa,根据[Q=σ-1/σmax]=227/50.419=4.502 3,计算得出的系数大于安全系数最小值1.15,所以该曲轴满足疲劳极限强度的要求。
3 有限元模态分析
3.1 有限元模态分析网格划分
设置体网格为2 mm,利用自动划分方法,进行网格化分,得出的有限元模型共划分单元74 941个、节点119 279个,如图7所示。
3.2 振动方程
计算得出曲轴的固有频率和固有振型是曲轴模态分析中的主要任务。由于曲轴结构阻尼比较小,对其固有振型影响不大,人们可以忽略该参数[12],将其简化为无阻尼振动系统,则有振动微方程:
将特征方程系数项展开,得到一个与[ω2]有关的[n]次多项式,解出该多项式就能得到曲轴的固有频率,再将固有频率带入式(4),就可解得曲轴特征向量,获得给定振动频率下的曲轴振型图。
3.3 自由模态
在进行曲轴振动特性分析时,自由模态分析是研究的一种方法。曲轴固有振动模态与自己的材料和结构有关,而与所受外部约束及外部载荷无关,因此不加载其他约束即可进行曲轴模态分析,为后续曲轴可靠性分析奠定基础。在对曲轴的固有频率进行分析时,通常用弹性绳吊起,让曲轴处于自由状态,因此在进行有限元自由模态分析时,不加载其他约束来分析曲轴的自由模态[13]。
3.4 约束模态
为了防止曲轴发生共振现象,研究曲轴的固有频率和固有振型是很有必要的,对曲轴施加附加约束进行模拟分析,研究结果将更接近曲轴的实际情况。在主轴承和纵向止推轴承的作用下,曲轴运动受到约束,其中止推轴承迫使曲轴不发生轴向位移,由于曲轴有滑动轴承与6个主轴颈配合,因此需要在曲轴的6个主轴颈处施加无摩擦约束[14]。曲轴运动时,除了要保证轴向位移,还要预留一定范围满足曲轴在温度作用下的尺寸变化要求,所以在曲轴结构上只能施加一处轴向定位[15]。
3.5 计算结果与分析
下面进行曲轴固有频率分析。曲轴的振动主要由发动机在运行时的低阶频率激励引起,因此只需要通过分析曲轴的低阶模态来研究发动机激发振动[16]。本文应用ANSYS Workbench软件对曲轴的前8阶振动模态进行了分析,计算固有频率的结果如表4、表5所示,其中,表4为无附加约束的自由振动固有频率,由于在无附加约束时,曲轴前6阶固有频率几乎为0,故表4显示的是7至12阶自由振动固有频率;表5为有附加约束的振动固有频率。
其中,由于自由模態的前6阶及约束模态第1阶固有频率几乎为0,所以可认为是曲轴刚体振动,可以忽略。对比表4和表5可以看出,曲轴在有附加约束条件下的固有频率比无约束条件自由振动的固有频率大很多。如表5所示,最大变形出现在第7阶振动,从应变图中可发现其最大变形表现为曲轴的弯曲变形,如图8所示。从表5可以得到,在有附加约束的条件下,该曲轴最小固有频率为1 180.2 Hz,如果取V10发动机曲轴的转速为3 000 r/min,在该运行工况下,其转动基频为50 Hz,而此时曲轴的最小固有频率远远大于该转速下的基频,所以该曲轴可在发动机运行时避免发生共振现象,满足曲轴振动特性的设计要求。
4 结语
本文采用Solid Works软件完成曲轴建模,利用了ANSYS Workbench完成发动机曲轴静力学有限元分析,获得曲轴的应变和应力分布云图。其间对该曲轴进行结构强度分析,得出不同气缸发火时,最大应力值出现在第一气缸发火时,应力值为50.419 MPa,最小应力值出现在第三气缸发火时,应力值为23.221 MPa,根据疲劳强度校核,计算得出的曲轴安全系数大于要求的最小安全系数,因此可认为该曲轴满足结构强度要求。
从上述各气缸发火时计算结果及应力应变云图可知,在气缸发火时,位于曲轴两端的各曲拐主轴颈及连杆轴颈应力应变均较小;发火时,对应的气缸内,应力及应变最大的位置出现在曲柄连杆轴颈的过渡圆角处以及主轴颈的过渡圆角处,因此可认为此处为曲轴疲劳强度的最弱环节。可以推断,曲轴的曲柄连杆轴颈的过渡圆角处与主轴颈的过渡圆角处容易发生疲劳损伤,甚至是疲劳断裂失效,在优化设计时应注意这些区域,改善应力应变情况。
本文采用ANSYS Workbench分析了曲轴前8阶模态,获得了前8阶固有振型。从该曲轴的各阶模态可以得出结论,曲轴的所受的激励频率远小于曲轴的最小固有频率,不会发生共振现象,符合振动特性设计要求。
从振型图可以看出,曲轴的最大变形表现为曲轴弯曲变形,在优化设计时应注意这些地方,以改善曲轴的振型,避免因共振引起的失效。
参考文献:
[1]贺洋洋,申琪,郭昌盛,等.汽车发动机曲轴有限元分析及优化设计[J].陕西理工大学学报(自然科学版),2018(2):7-11.
[2]陈大荣.船舶内燃机设计[M].北京:国防工业出版社,1995.
[3]明章杰.柴油机曲轴系统动态特性与冲击响应研究[D].大连:大连理工大学,2008.
[4]黄硕.发动机曲轴静态性能和模态分析[J].汽车工艺师,2014(10):54-57.
[5]Raub J,Jones J D,Kley P,et al.Analytical Investigation of Crankshaft Dynamics as a Virtual Engine Module[J].Sae Transactions,1995(412):1990-2002.
[6]郭磊,郝志勇,刘波.曲轴强度多体动力学与有限元子模型法仿真[J].浙江大学学报(工学版),2009(9):1638-1643.
[7]李静,王东方,缪小东,等.发动机曲轴扭振仿真分析与研究[J].机械设计与制造工程,2017(5):41-45.
[8]施兴之,肖金生.连杆有限元分析的边界条件的研究[J].武汉理工大学学报(交通科学与工程版),1994(2):122-127.
[9]郝伟.利用ANSYS软件对曲轴的受力进行分析[J].甘肃科技,2009(18):51-52.
[10]陶文辉.某型16 V柴油机曲轴的强度计算及性能分析[D].哈尔滨:哈尔滨工程大学,2008.
[11]黄建余,牛晓晓,李晓波,等.某大功率柴油机曲轴及主轴承受力和运动分析[J].节能技术,2012(2):136-141.
[12]蔡玉强,赵闯.基于Workbench某V12发动机曲轴有限元模态对比分析[J].华北理工大学学报(自然科学版),2018(4):88-93.
[13]周海超,左言言,鲍林晓.四缸柴油机曲轴的自由模态分析[J].噪声与振动控制,2010(6):63-66.
[14]Mourelatos Z P.SAE Technical Paper Series [SAE International SAE Noise and Vibration Conference and Exposition - (MAY.15,1995)]SAE Technical Paper Series - An Analytical Investigation of the Crankshaft -Fly wheel Bending Vibrations for a V6 Engine[J].Sae Transactions,1995(1):951276.
[15]付贵,郭湘川.基于ANSYSWorkbench的某活塞发动机曲轴有限元模态分析[J].科技创新与应用,2018(6):20-21.
[16]陈龙.发动机曲轴耦合振动分析及控制技术研究[D].重庆:重庆理工大学,2015.

