层理性页岩声波各向异性校正方法研究

李贤胜，刘向君，梁利喜，李 玮，高 阳，熊 健

（1.西南石油大学油气藏地质及开发工程国家重点实验室，四川成都610500；2.中国石油新疆油田分公司勘探开发研究院，新疆克拉玛依834000）

页岩气是重要的非常规油气资源，在我国地质储量丰富，可采储量巨大[1-2]。页岩各向异性通常是由定向排列的黏土矿物和微裂缝导致的，页岩的力学、声波等属性表现出各向异性特征[3-5]，部分页岩弹性各向异性可达51%[6-7]。除黏土矿物和微裂缝外，层理也是导致页岩各向异性的主要成因之一，尤其层理性页岩，即便其基质和层理的各向异性较弱，层理性页岩整体上仍表现出一定的各向异性，且各向异性程度与层理方向、层理密度相关[8-9]。页岩声波各向异性会导致同一页岩地层沿不同测量方向表现出不同的声学特性。为实现页岩气高效开采，大斜度井、水平井已成为页岩气勘探开发的主要井型[10-11]，而受页岩各向异性的影响，在水平井、大斜度井和直井中，即便是同一页岩地层，其声波测井响应仍存在较大差异[12]，对页岩储层测井评价方法和标准的建立及评价效果产生影响，进而影响基于测井数据的井震反演及地层压力预测等研究，因此，有必要开展页岩地层水平井声波各向异性校正方法研究。

关于各向异性校正方法的研究相对较少。HORNBY 等[13]提出椭圆方程理论进行声波各向异性校正，该方法假定深度相近，分布相似的页岩声学性质相似，且各向异性系数难以获取。乔悦东等[14]针对椭圆方程理论中各向异性系数难以获取的问题，提出采用最小二乘法计算Thomsen 各向异性系数，并开展纵波各向异性校正。刘劲歌等[15]综合分析纵波各向异性与围压、泥质含量关系，提出了线性-指数校正公式计算纵波各向异性系数，该方法仍基于椭圆方程理论进行声波校正。时建超等[16]选取研究区纯砂岩层的水平井、直井声波测井响应，用数理统计方法建立了经验校正公式，该校正方法在研究区应用效果较好，但仅适用于纯砂岩，且具有地区适用性。龙马溪组页岩作为我国海相页岩气的主要产层[17]，层理发育，结构复杂[18]，开展该地层声波各向异性校正研究，有利于指导该区块页岩气井施工及测井储层评价。

首先，以数值模拟实验的方法分析了层理性页岩声速各向异性与层理方向、层理密度的关系；然后，通过曲线拟合的方法对所得关系进行函数表征；接着，依据所得函数式建立了声速各向异性校正公式，实现将水平井、大斜度井的声波测井响应校正到直井响应；最后，通过将该校正公式应用于SC 盆地CN 区块龙马溪组页岩水平井声波测井响应校正以说明方法的适用性。

1 各向异性校正方法

相较于室内声波实验，声波数值模拟实验能更好地对层理性页岩声波响应进行分析，从而得到层理角度、层理密度对声波时差的影响。因此，首先，基于数值模拟实验，开展不同层理角度、层理密度的二维页岩声波时差测试；接着，基于数值模拟实验结果处理得到不同层理角度、层理密度下的纵波各向异性系数，进而分析层理性页岩层理密度、层理角度对纵波各向异性系数的影响规律；然后，将层理角度、层理密度对纵波各向异性系数的影响规律进行表征，得到纵波各向异性校正模型。以下详细介绍声波数值模拟方法及二维页岩模型，并分析层理对声速各向异性系数的影响。

1.1 数值模拟方法

基于Matlab 编制程序完成二维页岩声波数值模拟研究。以U表示二维空间任意时刻任一点处的位移，以V表示纵波的传播速度，则可以推导得到二维声波波动方程，对二维声波波动方程进行差分，构建边界条件及稳定性条件，并赋予初始条件，就可以对差分方程进行求解。

1）波动方程

某一时刻t，二维空间上（x，y）处的位移U（x，y），推导可得二维声波方程为：

式中：V（x，y）表示纵波的传播速度，对二维波动方程作离散化处理，得其差分表达式：

式中：Δx为差分网格的水平间距，Δy为差分网格的垂直间距，Δt为时间步长。

2）边界条件

二维页岩模型的上下边界设置为吸收边界，左右边界设置为常规反射边界，即在左右边界上的点位移为0。

3）稳定性和收敛性条件

要使差分方程的解稳定，则差分方程解的误差需要满足不随时间的增加而增加，即需要满足：

4）初始条件

对于有限差分方程，需要赋予初始值就可以求解任意时刻任意位置的值。在零时刻，位移速度为0，即初始条件为：

震源信号采用数值化的纵波探头信号，并将震源信号添加在二维页岩模型上边界中点处，接收点设置在下边界中点处[19]。

5）数据处理

数值模拟记录声波从激发点到接收点的传播时间，用二维页岩模型的长度比上传播时间，则可得到页岩模型声波时差：

式中：ΔT为页岩模型声波时差，μs/m；T为声波在页岩模型中的传播时间，μs；L为二维页岩模型长度，m。

1.2 数值模型

层理性页岩的层理方向和层理密度是影响其声波各向异性的重要因素[20]，借助数模方法研究层理方向和层理密度对页岩声波各向异性的影响。为与物理实验相匹配，构建边长为50 mm 的正方形二维页岩数值模型，x、y方向各取500 个网格，网格精度为0.1 mm；时间网格取3 000，时间精度设置为0.01 μs。等间隔设置页岩基质和页岩层理，层理厚度设置为0.2 mm，依据研究区典型页岩参数将二维模型中页岩层理的声波速度设置为1 825 m/s，将二维页岩模型中页岩基质设置的声波速度设置为5 250 m/s。分别建立层理角度为0o（平行层理面）、10o，20o，30o，40o，50o，60o，70o，80o，90o（垂直层理面），层理密度为0.4，0.6，0.8，1.0，1.2 条/mm 的二维正方形页岩模型。模拟计算不同条件下超声脉冲从激发器到接收器的传播时间，计算得到各种情况下超声波在层理性页岩中的声波时差。

1.3 层理对声速各向异性的影响

目前表征弹性各向异性的主要参数是Thomsen参数，然而，Thomsen 参数仅表征声波传播方向垂直层理与平行层理两种角度下的声波速度差异，而不能表征其他角度下的声波差异大小，即仅适用于讨论直井与水平井之间波速响应差异。为了将各向异性参数扩展至井斜角任意的大斜度井，采用比值法各向异性系数K：

式中：ΔT(θ)为一定层理角度下的页岩声波时差值，μs/m；ΔT0为声波方向平行层理面的声波时差值，μs/m。

比值法各向异性系数考虑了多种层理角度时的声波各向异性，适用的角度更广，在一定程度上起到了归一化的作用，以减弱岩样差异的影响。根据各向异性系数定义，K 值取值越接近于1，此方向上各向异性越弱，即此方向上声波速度越接近于平行层理方向的速度。当层理角度为0o 时，各向异性系数K为1；当层理密度为0（即不存在层理）时，岩心整体呈各向同性性质，则各方向上的各向异性系数K都为1。

基于数值模拟实验结果分析层理角度、层理密度对声波各向异性的影响。首先分析层理密度对纵波各向异性的影响。层理角度为10o，30o，50o，70o，90o时数值模拟结果见图1。当层理角度为10o时，随着层理密度从0.4条/mm增加到1.2条/mm，纵波各向异性系数呈近似线性从1.02 增加到1.05；当层理角度为90o时，层理密度从0.4条/mm增加到1.2条/mm，纵波各向异性系数从1.07 增加到1.22。层理密度较低时，层理角度的增加导致各向异性系数的增加量更小；层理密度较高时，随层理角度增加各向异性系数的增加量更大。此外，低层理角度岩心之间纵波各向异性系数差异大，而高层理角度岩心之间纵波各向异性系数差异较小。

图1 纵波各向异性系数与层理密度变化关系Fig.1 Crossplot of longitudinal wave anisotropy coefficient against bedding density

接着分析层理角度对各向异性的影响，依据数值模拟结果绘制层理角度的正弦值与纵波各向异性系数交会图（图2），可见随层理角度增大，纵波波速呈递减趋势[21]，纵波各向异性系数增大。纵波各向异性系数介于1 ～1.23。层理角度为0o时各向异性系数最小，层理角度为90o时各向异性系数最大。同一层理密度条件下，随着层理角度的增加，纵波各向异性系数逐渐增大。当层理角度较低时，由层理密度的差异导致纵波各向异性系数的差异较小，随着层理角度的增加，不同层理密度导致纵波各向异性系数差异增大。由此，建立各向异性校正关系式时，需同时考虑层理密度和层理角度。

图2 纵波各向异性系数随层理角度变化关系Fig.2 Crossplot of longitudinal wave anisotropy coefficient against bedding orientation

2 校正模型构建

构建校正公式的方法是首先通过数学函数对数值模拟所得单趋势规律进行表征，得到相同层理密度下层理方向与各向异性系数的关系；然后再引入层理密度值，得到能够同时表征层理密度和层理方向影响的模型。

分别用线性形式、指数形式、幂函数形式及二次多项式形式最小二乘拟合，然后比较拟合线与趋势线的关系，以层理密度为1.0的趋势线为例（图2中棕色正方形点），纵波各向异性系数与角度正弦值关系中，幂函数形式相关系数最低，R2为0.874 4，指数形式和线性形式拟合效果相对较好，相关系数R2分别为0.980 2、0.975 8，二次多项式的拟合效果最好，相关系数R2达到了0.999 4（图3）。因此，构建层理角度与纵波各向异性之间关系可用二次多项式形式来表征：

式中：Kc为纵波各向异性系数；θ为层理角度，（o）。

图3 纵波各向异性系数与层理角度函数关系Fig.3 Relation between longitudinal wave anisotropy coefficient and bedding orientation

依据式（7），层理密度一定条件下，层理角度与纵波各向异性系数之间的关系可用二次多项式形式表征。当层理密度不同时，需要对式（7）进行一定修正，使其能够考虑层理密度的影响，采取的方式是在公式中添加层理密度系数m，由于层理角度一定时各向异性系数与层理密度呈线性关系，故将层理密度参数以下式形式添加，使得：

式中：m为层理密度系数，条/mm。

依据式（7）可以对图2中所示数值模拟实验结果进行函数表征（图4），图中数据点为数值模拟实验结果，实线为式（8）计算结果。在5种层理密度条件下，随着层理角度的增加，数值模拟实验结果（数据点）与校正式计算结果（实线）增长趋势一致，且吻合度较好，说明构建的校正关系式合理。由此，可得层理性页岩纵波各向异性系数与层理角度、层理密度的函数关系为：

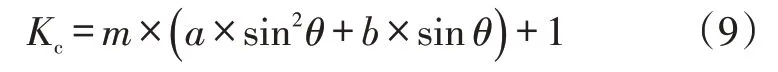
式中：a、b为待定系数，需要通过实验数据拟合得到具体值。构建的关系式满足层理角度或层理密度为0时，各向异性系数为1。

3 应用实例

图4 数值模拟实验结构与模型计算线对比Fig.4 Comparison of numerical simulation experiment and model calculation line

将建立的层理性页岩波速各向异性校正公式应用于SC 盆地CN 区块A1 井龙马溪组优质储层段水平井声波测井响应校正中来说明方法的有效性。该储层段岩性为层理性页岩，直井目的层深度范围为2 506 ～2 513 m，水平井同一层位深度为2 872 ～2 920 m，从井斜曲线上可得页岩目的层深度段，水平井井斜角为76°～80°。

为了检验基于数值模拟构建的校正式的可靠性，选取SC 盆地CN 区块井下龙马溪组优质储层段页岩岩心（2 505.97 ～2 566.70 m），开展室内页岩纵波测试。岩样外观上呈现黑色，层理发育。依据实际水平井井斜角范围（76°～80°），物理实验中将井下页岩岩样加工成层理角度为45o、60o、75o的立方体岩心，岩心尺寸为50 mm×50 mm×50 mm（图5、图6）。

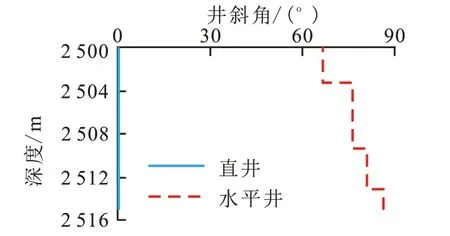
图5 目的层水平井与直井井斜角曲线Fig.5 Deviation curve of horizontal wells and vertical wells

图6 页岩岩心照片及示意图Fig.6 Photograph and diagram of shale cores

实验设备为西南石油大学SCAR-II 高温高压全直径多参数测定仪。该仪器声波测试为脉冲透射法，示波器时间精度为0.01 μs。室温下，将岩心装入釜体后，增加围压至地层围压并完成纵波测试，记录首波初至时间，实验数据见表1。岩心密度介于2.50 ～2.54 g/cm3，岩心观察得到岩样层理密度分布在0.60 ～0.65 条/mm，通过测量平行层理方向与层理方向成45o、60o、75o方向岩心波速值来获取对应方向的各向异性系数Kc，纵波各向异性系数介于1.088 ～1.109。

表1 物理实验数据Table1 Physical experiment data

依据式（9），首先确定层理密度系数，实际实验岩心层理密度平均为0.62 条/mm，故在计算中m值取为0.62，再通过函数拟合的方式得到a、b值（图7）。由式（9）可得纵波各向异性校正公式如下：

式中：DTC为水平井测井纵波时差值，μs/m；DTC0为校正后水平井纵波时差值，μs/m。

图7 物理实验与模型计算线对比Fig.7 Comparison of physical experiment and model calculation line

同一层段水平井与直井井斜曲线差异明显，水平井井斜角分布范围为66o～86o，直井井斜角分布范围为0.796o～0.974o，方位曲线差异较小。校正前，测井曲线上水平井纵波时差分布范围为207.6 ～229.2 μs/m，直井纵波时差分布范围为235.7 ～264.8 μs/m（图8），正态分布图上表明水平井纵波时差中心值为217.2 μs/m，直井纵波时差中心值为245.3 μs/m，两者差异明显（图9）。分别用文献校正方法和文中校正方法对该井纵波时差曲线做校正，效果如图8所示，经式（10）校正后，纵波时差曲线与垂直井纵波时差曲线接近，校正后的纵波时差测井曲线分布在垂直井测井曲线周围，用文献校正方法校正量不足，校正后的纵波时差曲线与直井纵波时差曲线差异仍然明显。水平井纵波时差分布范围为234.1 ～258.4 μs/m，正态分布图中心值为245.1 μs/m，用文中校正方法校正后的水平井纵波时差与直井纵波时差相接近，表明校正效果较好。

图8 CN区块A井测井曲线Fig.8 Well logging curve of well-A in CN block

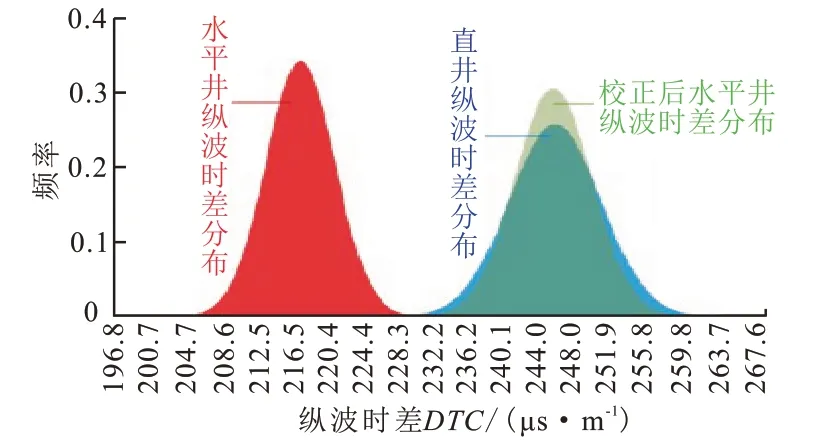
图9 各向异性校正前后纵波时差值正态分布Fig.9 Normal distributions of interval transit time of longitudinal wave before and after correction for anisotropy

文中所提校正方法校正后纵波时差曲线与垂直井纵波时差曲线并不完全重合，部分井段存在差异，主要是因为直井与水平井钻遇的同一地层也会存在差异，另外围岩厚度及井眼轨迹等对水平井和直井测井影响程度不同，因而文中校正方法将水平井测井响应校正为与直井响应规律一致，为基于直井的解释方法的水平井测井解释做出一定的贡献。

4 结论

基于数值模拟方法分析了层理角度、层理密度对页岩声波各向异性的影响，构建了层理性页岩声波速度各向异性校正方法，并通过在长宁区块龙马溪组层理性页岩地层的应用说明了方法的有效性，取得认识如下：

1）层理性页岩会表现出明显的各向异性特征，会导致同一页岩地层在水平井纵波时差值显著高于直井中纵波时差值，不利于区域储层定量评价等，各向异性校正是必要的。

2）层理密度和层理角度是影响层理性页岩各向异性的重要因素，随着层理角度、层理密度的增加，纵波各向异性增强。纵波各向异性系数与层理角度的正弦值之间近似满足二项式规律。

3）实例应用表明本文所提纵波各向异性校正方法能有效地将水平井纵波时差值校正为直井纵波时差值。