计及杆塔绕流效应的风速模型及其对风电机组输出功率的影响研究
安 琪,梁定康,韩肖清,王 鹏
(太原理工大学 电力系统运行与控制山西省重点实验室,太原030024)
近年来,风电场研究和建设取得了很大进步,各种因素影响下的风电机组风速模型研究已经较为成熟。文献[1]建立了山体地形下的尾流风速模型,文献[2]研究了随机风向下风电场的风速分布,并提出一种风向坐标变换法解决尾流遮挡面积计算困难的问题。
随着风电装机容量的逐年增加,风电场所在地微环境对风电场风速的影响日益凸显,进而影响风电机组输出功率,其中风电场中存在众多传输电能的混凝土结构电力杆塔,不合适的杆塔位置对风电机组输出功率的影响不可忽视,这一点已被风电场工程实践与运行证实。2016年对实际风电场的调研结果表明:在特定情况下风力发电组的输出功率与理论计算值之间的差异性较大,通过详细统计每台风电机组的风况和功率,发现当杆塔处于某一机组迎风方向时,该风电机组输出功率明显降低。因此,为了评估杆塔对风电机组输出功率的影响,有必要研究风电机组杆塔绕流效应,然而关于风电机组杆塔绕流的理论建模尚待研究。
在空气动力学研究中,对自然风经过障碍物形成的绕流模型已经成熟。BREUER[3]提出了大涡模拟法对障碍物绕流进行数值模拟,TUTAR et al[4]提出一种模拟两个平行障碍物周围风场的RNG子网格尺度模型,文献[5]提出了能够模拟不同形状障碍物的格子玻尔兹曼绕流理论。但是绕流理论尚未应用到风电机组杆塔绕流模型中,为了分析杆塔布局对下游风电机组输出功率的影响,需要建立风电机组的杆塔绕流效应模型。首先需要研究如何对杆塔的形状进行简化。文献[6]以直立式码头为例,通过空间的离散化仿真对码头中的桩柱进行三维数值模拟,得到空间分布速度云图,并与文献[7]的圆柱绕流模拟结果进行对比,研究表明:Fluent圆柱绕流理论[8]能够近似地模拟杆状物体绕流的风速分布,即,将杆塔近似为圆柱体进行绕流分析是合理的。詹昊等[9]用雷诺数对不同风速和柱体直径下的圆柱绕流进行分类,并确定杆塔绕流处于亚临界雷诺值。
本文将绕流现象融入山体地形和随机风向中,详述杆塔绕流对下游风电机组输出功率的影响。基于亚临界雷诺值建立风吹过杆塔后的动态时序非定向风速模型[10](非定向:风经过杆塔后的风向可能存在正向和逆向两个方向),并将杆塔绕流模型与经典的风电机组影响因素结合,建立考虑杆塔绕流的风电机组风速模型。
1 杆塔对风速的遮挡模型
风电机组的输出功率和风电机组的输入风速有直接关系。为了准确评估风力发电机组输出功率,在以往的风电机组风速模型基础上增加电力杆塔的绕流模型,对风速进行细化分析,进而通过风速-功率模型计算风电机组的输出功率。
1.1 障碍物绕流特性
风吹过有限长圆柱后的一段距离内风速和风向发生变化,从而产生绕流效应[11]。本文将杆塔近似为圆柱体进行绕流分析[3],参考亚临界雷诺值下的圆柱绕流仿真结果对杆塔的风速绕流进行建模。亚临界雷诺值下整个圆柱绕流区域的风场趋向于稳定,因此,杆塔绕流的风速研究忽略绕流所造成的风向变化,认为风吹过杆塔仅会对下游风速的大小产生影响。
图1为有限长圆柱的绕流影响示意图。来流风v0与x轴方向相同,y轴垂直于来流风向,v轴表征风速大小,D为杆塔的直径,设定下游尾流区长度为30D,即来流方向的绕流影响距离为30D;y轴展向长度为20D,即垂直来流方向上杆塔两侧绕流影响距离分别为10D[12].

图1 障碍物绕流影响示意图Fig.1 Diagram of obstruction flow effect
图1 中,x-v平面上曲线vx为y=0处的风速特性曲线[9]。可以看出,在风经过杆塔之后,由于障碍物的绕流特性,风在刚经过杆塔时的一段区域内风向与来流方向相反,并且随着距离x的增加,大小逐渐趋近于初始风速v0.y-v平面上的曲线vx,y为x恒定时,沿y轴方向的风速特性曲线。在x恒定的某一空间位置,绕流风速vx,y随着y绝对值的增加而增大。
1.2 杆塔的风速遮挡模型
在图2所示的水泥杆塔中,杆塔的直径为d1,上部横担的直径为d2,杆塔高度为H,为了方便计算,可将杆塔等效为上粗下细的圆锥台形状物体。由于现有的障碍物绕流理论中缺乏圆锥体的绕流研究,因此本文中按照体积相等的原则进一步将圆锥等效为直径为D,高度为H的圆柱体,并参考圆柱绕流理论对杆塔的绕流模型进行建模。
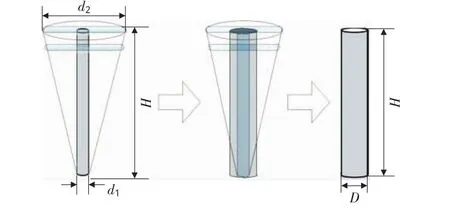
图2 杆塔的等效模型Fig.2 Equivalent model of cement tower
参照图1坐标系统,通过大涡模拟法对风速绕流进行数值模拟,得到图3的风速绕流曲线[13]。根据来流风的方向距杆塔的远近,将风经过杆塔后的影响区域划分为绕流区、过渡区和稳流区,图3(a)为y=0时沿x轴的风速vx的变化特性曲线。其中,x=2D处风速为0,为绕流区和过渡区的临界点;x=20D处为过渡区和稳流区的临界点。绕流区、过渡区和稳流区内沿y轴的风速变化趋势不同,图3(b)为x坐标为x=x0时,沿y轴的风速vx0,y的变化特性曲线,其中y=0时的风速为vx0,m1和m2的值分别为m1=1.3vx0,m2=
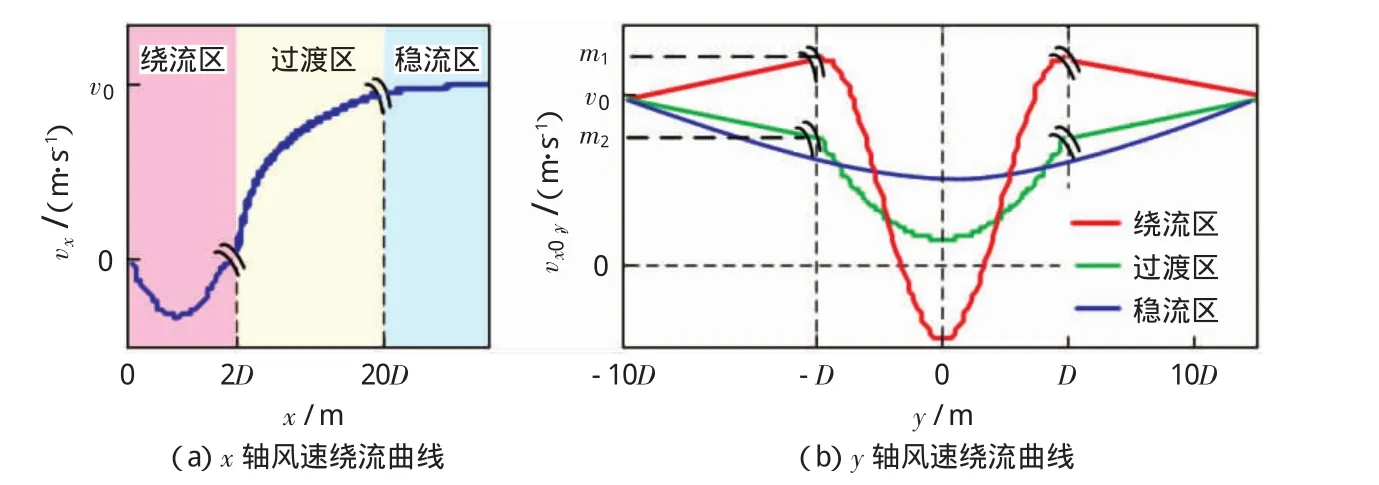
图3 风速分别沿x和y方向的变化特性Fig.3 Wind speed curve along the xaxis and yaxis
由图3(a)中沿x轴方向的风速变化曲线,将x轴上风速vx的值拟合为:
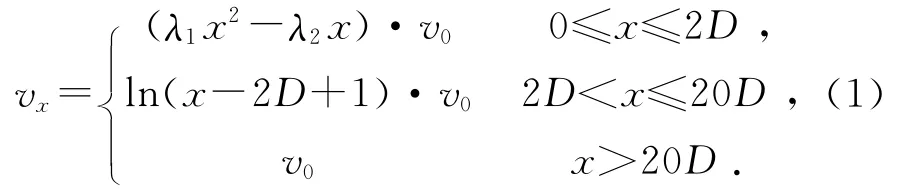
式中:λ1为空气密度修正系数,反映了风速衰减的幅度,λ2为摩擦系数,与杆塔的材质有关。由图3(a)的风速拟合曲线计算得到λ1=0.3,λ2=0.6.
得到x=x0处的风速vx0后,进而通过图3(b)中沿y方向上的风速变化曲线,即vx0,y风速曲线,可以得出空间内任意位置(x0,y0)处的风速vx0,y0.依据图3(b)的风速变化曲线拟合可知:绕流区、过渡区和稳流区内的风速变化分别遵循不同的函数变化规律。
绕流区内沿y方向的风速变化曲线为分段函数,vx0,y曲线拟合的计算公式为:
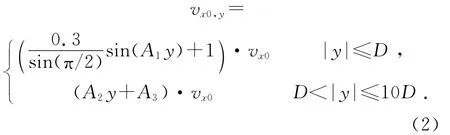
式中:A1,A2,A3为绕流区的特征参数,由绕流区风速变化曲线拟合计算所得:
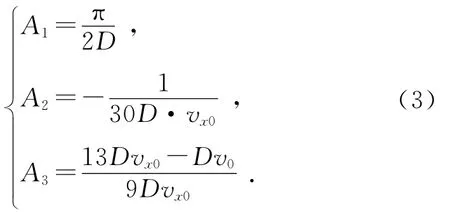
过渡区内,vx0,y的风速变化曲线拟合的分段函数为:

式中:B1,B2,B3为过渡区的特征参数,由过渡区风速变化曲线拟合计算所得:
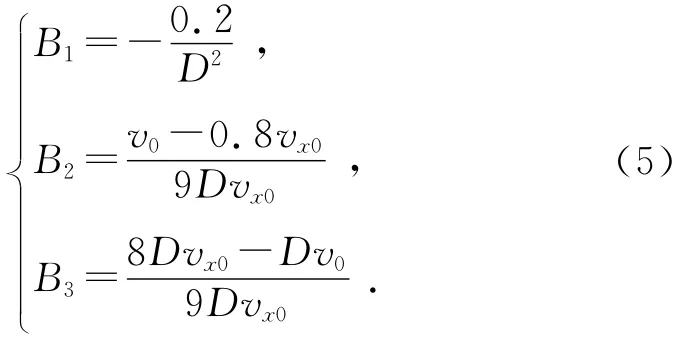
稳流区内,vx0,y的风速变化曲线拟合函数为:

式中:C为稳流区特征参数,由稳流区风速变化曲线拟合计算所得:
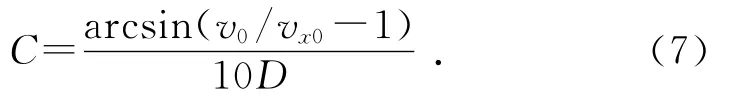
为了表征风经过杆塔后的衰减特性,设定杆塔的风速衰减系数dt为:

2 不同因素时杆塔对风电场输出功率的影响
经典的风电机组输出功率研究表明,风电机组的尾流效应、山体地形、随机风向等经典因素会对下游风电机组造成影响[14]。
2.1 不计及杆塔绕流的经典风电机组风速模型
传统风电场中,综合考虑尾流、山体地形和随机风向的风速模型如图4所示。其中,x1为上游机组到下游机组的距离,蓝色区域为尾流的影响范围,r为风电机组的叶轮半径,rw为上游风电机组尾流投影在下游机组平面的尾流影响半径,Δh为上游风电机组与下游风电机组的高度差,φ为上游机组尾流影响范围的边缘线与来流风向的夹角,自然风速下tanφ取0.04.上游风电机组的初始风速为v0,v1为上游机组尾流影响下的风速。蓝色阴影部分为上游风电机组对下游机组的尾流遮挡面积Aj,详细计算公式见文献[1].
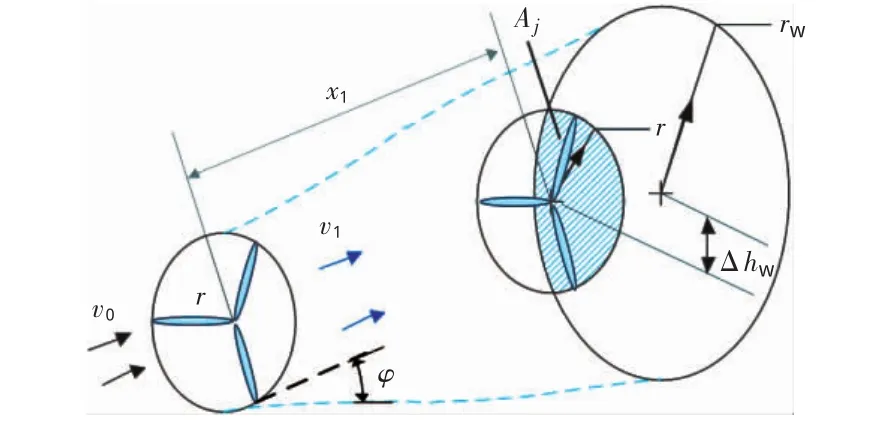
图4 风电机组尾流效应Fig.4 Wake effect of wind turbine considering tower flow
尾流风速v1与初始风速v0的关系为[2]:
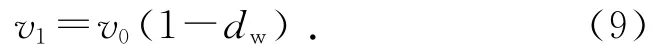
式中:dw为风电机组尾流的风速下降系数。综合风电场中每台风电机组单独对下游机组WTi影响时的尾流风速和遮挡面积,可以求出每台风电机组的等效输入风速
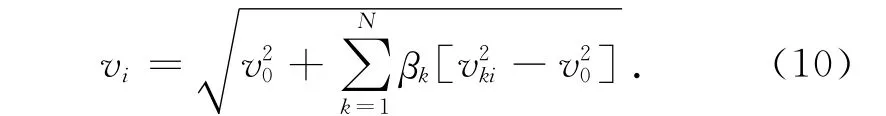
式中:βk为遮挡系数,βk=Ajk/Ari,Ajk为下游风电机组WTi被上游机组 WTk遮挡的面积,Ari=πr2为风电机组WTi的扫风面积,N为风电机组的数量总和,vki为被上游机组WTk影响下的WTi的风速,v0为自然风速。
为了方便求解不同风向下的遮挡系数βk,可采用坐标变换法确定上下游风电机组的迎风相对位置,描述风电机组的布局[14]。图5中,vref为参考风向西风;v′为风电场实际风速,与v的夹角为θ.
由图5可知,当风向由vref旋转θ角变为v′时,坐标轴旋转对应的θ角度,使实际风速v′与x′轴方向一致。此时上下游机组的相对位置发生变化,下游风电机组 WT2的坐标由(xj,yj)变为(x′j,y′j),坐标变换公式见式(11):
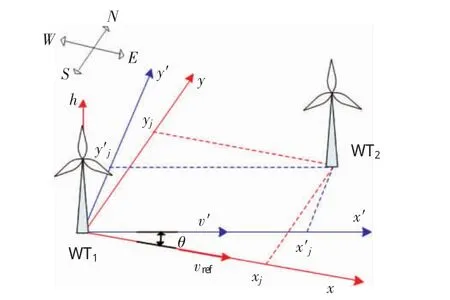
图5 风向坐标变换模型Fig.5 Coordinate transformation model of wind direction
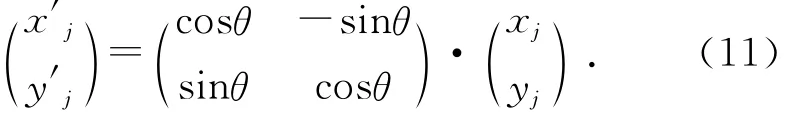
通过坐标变换方法,可以在任意风向下重新排列各风电机组的坐标位置,以保证风电机组永远处于迎风位置,从而简化了遮挡系数的计算。
2.2 计及杆塔绕流的风电机组风速模型
计及杆塔绕流效应的风电机组风速模型建立时可以参考风电机组尾流效应的理论,如图6所示,其坐标参照图1坐标系统。
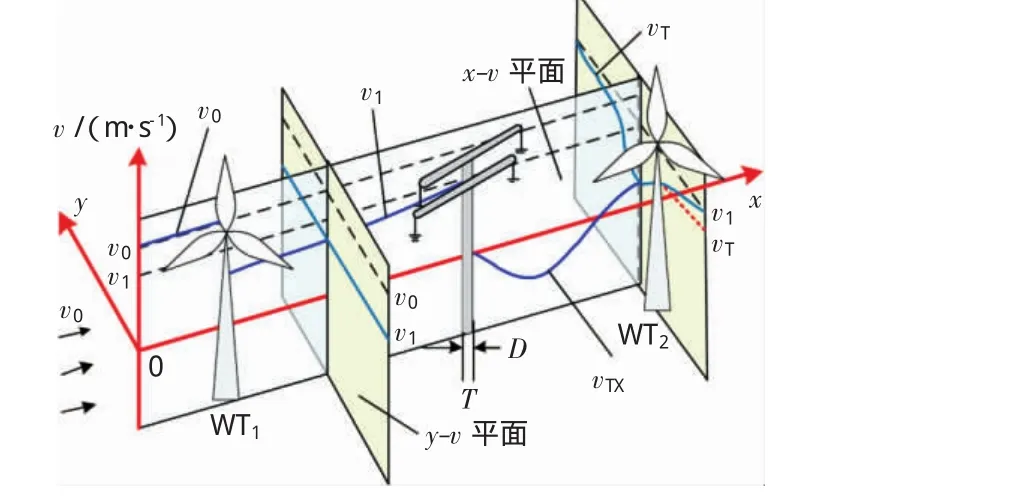
图6 考虑杆塔的风电机组尾流效应Fig.6 Wake effect of wind turbine considering tower flow
由图6可以看出,初始风速v0在经过上游机组WT1后,部分风能被WT1吸收,尾流部分风速大小降为v1;速度为v1的尾流风经过杆塔绕流后大小变为vT,vT的大小与杆塔和下游机组的相对位置有直接关系。vT和v1的关系为:
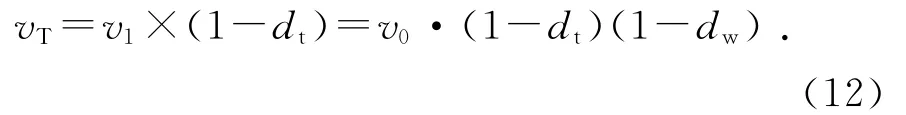
式中:dt为杆塔的风速衰减系数,见公式(8).
在山体地形和随机风向的影响下,杆塔和风电机组的相对位置发生改变,从而影响杆塔对下游机组的绕流遮挡面积以及下游机组的风速,如图7所示。图中,hW1和hW2分别为上下游风电机组的轮毂高度,hT为杆塔的高度,Δh为杆塔与下游风电机组的高度差。φT为杆塔绕流影响范围的夹角,计算公式为[15]:
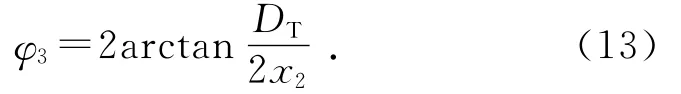
式中:x2为杆塔到下游机组的距离,DT为杆塔绕流在下游机组投影面积的宽度。
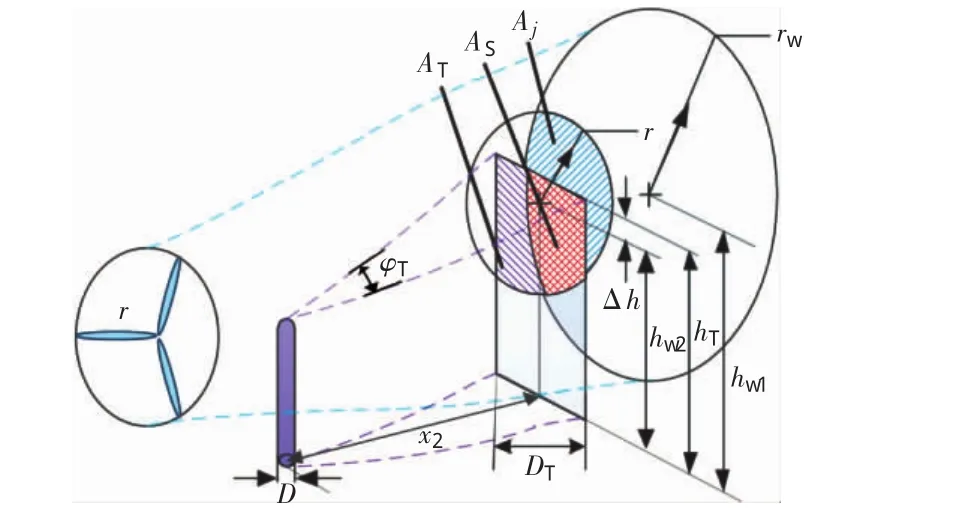
图7 计及杆塔、地形、随机风向的尾流与绕流效应Fig.7 Wake and flow effect considering tower,mountain terrain,and random wind direction
由图7可知,计算考虑杆塔的绕流影响时,可将遮挡模型分解为:上游风电机组单独对下游机组的影响模型,以及上游杆塔单独对下游机组的风速影响模型。蓝色阴影部分为上游风电机组对下游机组的尾流遮挡面积Aj,其计算已在2.1中得出;紫色阴影部分为杆塔单独对下游风电机组的绕流遮挡面积AT,计算方法见式(14),红色阴影为同时被上游机组和杆塔遮挡的面积。
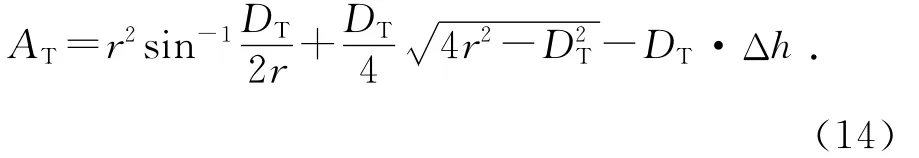
式中:
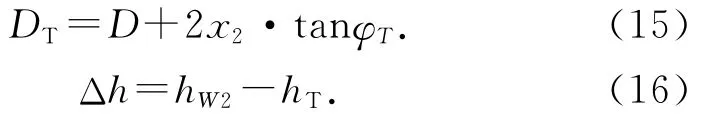
综合每台风电机组和杆塔单独对下游机组WTi的遮挡面积,可以求出每台风电机组的等效输入风速v[16]:
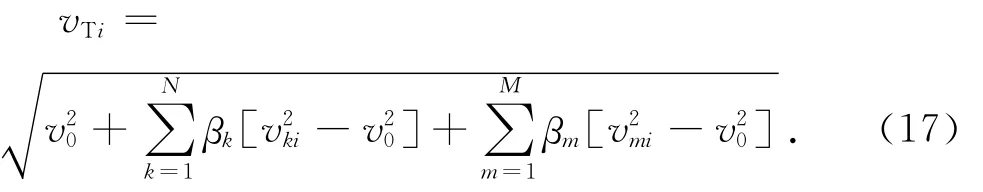
式中:βm为遮挡系数,βm=ATm/Ari,ATm为下游机组WTi被杆塔m遮挡的面积,M为风电场中的杆塔数量,vmi为杆塔m影响下的WTi的风速。
为了更方便地求解杆塔的绕流遮挡系数,该杆塔绕流风速模型采用2.1中的坐标变换法,得到各杆塔和风力发电机组的迎风方向坐标。
通过上述计算确定每台风电机组的等效输入风速后,参考经典的风电机组输出功率模型[17]计算考虑杆塔绕流效应的风电机组输出功率,仿真流程图如图8所示。
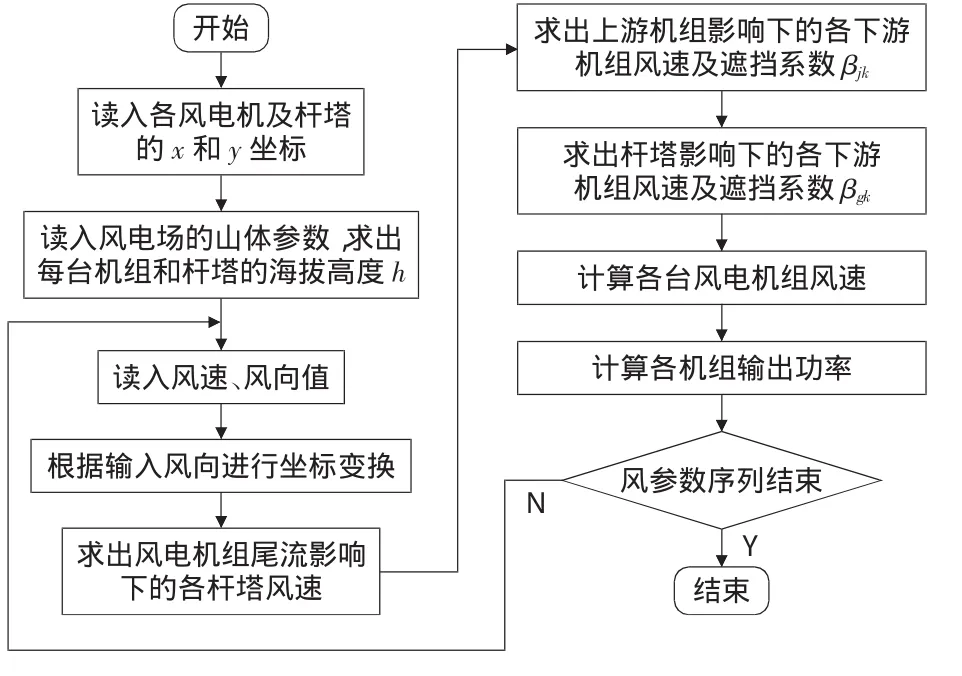
图8 仿真流程图Fig.8 Flow chart of simulation
3 算例分析
算例分析部分的框架结构如下:首先,算例3.1根据山西省某一风电场的实际地形(山体坡度)和风况(风速和风向),将考虑杆塔绕流与不考虑绕流时的风电场输出功率与风电场实测功率进行对比;其次,在算例3.2中,重点分析了以山体地形为变量的情况下,计及尾流效应时的杆塔绕流效应对风电场输出功率的影响;最后,在算例3.3中,分析了以随机风向为变量的情况下杆塔绕流效应对风电场输出功率的影响。
本算例选用型号为UP82/1500的风力发电机组,该机组的轮毂高度为65m,叶片长度为42.5m,机组的切入、额定、切出风速分别为3,10.8,25m/s.本算例中杆塔的高度、直径与绕流密切相关,因此选用高度为24m,直径0.55m的杆塔,其余参数见《35kV-220kV送电线路铁塔通用设计型录》,将杆塔等效为圆柱体后的圆柱直径为2.31m.风电场一年内的实测风向统计如图9所示,参考风向为西风,可看出该风电场主导风向为北风,因此采用北风作为基础算例的风向。
本算例中,将两个经典的单峰贝尔模型[18]进行组合,建立模拟风电场地形的双峰的贝尔模型,如图10所示。其中,双峰模型的参数如下:短峰的高度为300m,迎风坡面长度为200m;高峰的高度为500m,迎风坡面长度为200m,杆塔与对应风电机组的距离均为20m.在风电场中山头、坡地等面积狭小的区域,杆塔与风电机组间距离很短,杆塔绕流效应对下游机组产生影响。根据山西省某一风电场的实际情况,本算例拟定在风电场的33台风电机组中,7台风电机组处于山尖位置,2台风电机组处于山谷位置,这些位置处杆塔距风电场的位置较短,杆塔绕流对风电机组产生绕流影响。
3.1 基础算例
为了确定风电场中杆塔绕流效应对输出功率的影响,有必要建立考虑杆塔绕流效应的风电机组风速模型,计算风电机组输出功率并与风电场实测功率进行对比,从而确定杆塔绕流模型的必要性。本算例以山西省某一风电场的风机布局为基础,以2016年全年的实测风速风向为输入量,将考虑杆塔绕流效应的情况、不考虑绕流情况下仿真得到的风电场输出功率与实测功率进行对比,如图11所示。可以得出,风电场实际输出功率的平均值为7.94 MW,不考虑绕流时风电场的平均输出功率为8.59 MW,与实测功率相比提高了7.57%;而考虑杆塔绕流的风电场平均输出功率为8.17MW,与实测功率相比提高了2.81%.由此可得,考虑杆塔绕流效应的风速模型仿真得到的风电场输出功率更贴近风电场的实测功率,因此考虑杆塔绕流的风速模型能够更精确地预测风电场的输出功率。
3.2 山体地形对杆塔绕流的影响
本算例重点研究山体地形对杆塔绕流的影响,针对风电场山尖处的风电机组进行仿真,评估杆塔绕流对下游风电机组输出功率的影响。其中以山体地形为变量,风况参数和基础算例一致。通过等比例增加或减小基础算例山体模型中短峰和高峰的高度值,得到不同的山体坡度,评估山体坡度对杆塔绕流效应的影响。
本文认为功率变比可以更好地衡量杆塔前后功率的变化程度,功率变比的值越大,杆塔绕流对风电机组的削弱作用越强,为方便起见,做如下定义:

针对不同的山体坡度,计算风电机组的功率变比,结果如表1所示。其中,山体坡度0%为平坦地形,山体坡度100%为基础算例的山体地形,山体坡度50%即基础算例的山体基础上将山体坡度等比例减少50%.山体坡度150%即基础算例的山体基础上将山体坡度等比例增加50%.
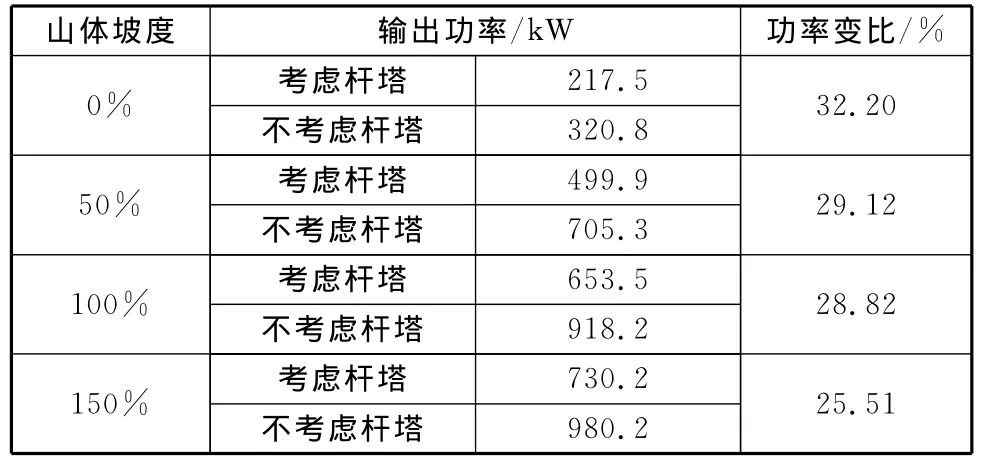
表1 不同山体坡度下的风电场功率变比Table 1 Conversion ratio of power output in different mountain inclination angles
由表1可见,当山体坡度为0%时风电机组的功率变比最大,为32.20%,当山体坡度为150%时功率变比最小,为25.51%,山体坡度与功率变比的大小成反比。由此可知,对于单台风电机组而言,杆塔绕流效应对单台风电机组输出功率影响严重,约30%左右;就消弭扰流效应而言,适当的山体坡度是有益的,山体坡度的增加,提高了杆塔和下游风电机组的相对位置,降低了杆塔对下游机组绕流效应的影响,从而降低了杆塔对输出功率的削弱作用。与经典的山体地形仅削弱下游风机的输出功率相比,山体坡度的存在避开了杆塔绕流对下游机组的影响,提高了下游风机接收到的风速,因此充分利用了风能,保证了下游风机输出功率最大。在未来风电场的规划中,需要综合考虑山体坡度对下游风机的双重影响(包括山体坡度对输出功率的提升作用、山体遮挡对风的降低作用),以风能利用率最大为目标,设计风电机组和电力杆塔的微观选址规划方案。
3.3 随机风向对杆塔绕流的影响
本算例重点研究随机风向下杆塔绕流效应对风电机组输出功率的影响,设定0°方向为西风,每10°为一个风向区间。在此基础上,针对不同的风向,通过输出功率的计算分析杆塔绕流效应对风电机组输出功率的影响。
本算例对不同风向下的风电机组绕流效应进行评估,如图12(a)所示,其中杆塔位于风电机组南侧。由图12(b)的仿真结果可看出,南风风向(遮挡风向)下杆塔会对下游机组产生遮挡,而北风风向下不产生任何绕流影响;当风向处于北风区时(图中黄色阴影部分),考虑杆塔情况下的风电场输出功率与不考虑杆塔时功率输出曲线重合,由此可见,杆塔对机组不产生遮挡。在南风区(图中绿色阴影部分),考虑杆塔绕流后的风电场总输出功率大幅降低,降幅约在30%左右。杆塔绕流效应在风向角为270°时最明显,输出功率从948.24kW 降低到642.94 kW,降低幅度高达32.19%.由上述分析可知,随机风向对考虑杆塔绕流效应的风电机组输出功率产生严重影响。因此在风电场的规划初期,应基于实测的风向数据,避免杆塔相对于风电机组的顺向排布,从而抑制杆塔绕流效应导致的风电机组输出功率波动,对杆塔和风电机组的微观选址有重要参考价值。
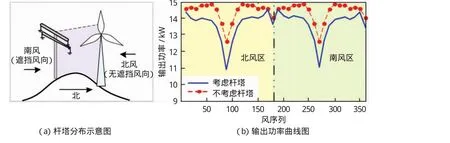
图12 随机风向对风电机组仿真结果Fig.12 Simulation results in various wind direction
4 结语
针对风电场中杆塔对下游风电机组的遮挡影响,提出了一种杆塔绕流风速模型,该模型结合风电机组间的尾流效应、山体地形和随机风向三个经典因素,计算杆塔绕流下的风电场输出功率,并与山西省某风电场的实测数据进行对比,评估了不同影响因素对杆塔绕流的影响。算例结果表明,在一些面积狭小的特定区域,杆塔对下游风电机组的影响是不可忽视的,研究成果对风电机组和杆塔的微观选址有重要参考价值。

