Investigating the effect of entrance channel mass asymmetry on fusion reactions using the Skyrme energy density formalism

M. M. Hosamani · A. Vinayak · N. M. Badiger

Abstract In the present investigations, the fusion crosssections for the formation of 200Pb compound nucleus(CN)using 16O + 184 W, 30Si + 170Er, and 40Ar + 160Gd nuclear reactions at energies above the Coulomb barrier were calculated to understand the effect of entrance channel mass asymmetry (α) on the fusion reactions; the Skyrme energy density formalism(SEDF)was used for this calculation.The SEDF uses the Hartree–Fock–Bogolyubov(HFB) computational program with Skyrme forces such as SkM*, SLy4, and SLy5 to obtain the nucleus-nucleus potential parameters for the above reactions. Using the SEDF model with SkM*, SLy4, and SLy5 interaction forces, the theoretical fusion cross-sections were determined above the barrier energy and compared with the available experimental fusion cross-sections. The results show a close agreement between the theoretical and experimental values for all selected systems at energies well above the barrier. However, near the barrier energies,the theoretical values were observed to be higher than the experimental values.

Keywords Skyrme force · Energy density formalism ·Hartree–Fock–Bogolyubov · Thomas–Fermi model ·Coupled-channel calculation

1 Introduction

The inter-nuclear potential is one of the most important factors to describe the heavy-ion nuclear reaction dynamics[1]. It is well known that the study of heavy-ion fusion reactions, in which the interacting nuclei effectively interact with each other,will probe the pre-saddle region as well as the field inside the Coulomb barrier extensively[2].Further, the study of heavy-ion nuclear reactions can provide major information about the barrier between the interacting nuclei, which hinders the synthesis of superheavy elements. Conversely, by studying the shape and size of the barrier distribution, the dynamics of the interacting nuclei can be investigated [3]. For a given system,the height and width of the barrier—in accordance with the semi-classical theory—remain same,and it is interesting to evaluate the effect of incident energy on such a barrier.Furthermore, theoretically, the reaction barrier is not very well defined and to some extent,it depends on the way it is calculated [4, 5]. For classical simplification, we are assuming that the interaction barrier is estimated from the interaction energy of the interacting nuclei,as a function of the relative distance (R) between them. However, the dynamical calculations of nuclear reactions were also performed by solving the classical equations of motion and using the liquid drop model [6, 7]. The estimated fusion barrier is also a deciding parameter for evaluating the probability of interaction of the heavy ions.In other words,the fusion barrier height and width are the deciding factors to evaluate the probability of fusion reactions. Therefore,the aim of the present investigations is to calculate the interaction potential using the energy density formalism(EDF) [8] with Skyrme forces [9]. Considering this, the total energy of the fermions of the system is given as a function of the one-body density [10]. Further, different Skyrme force gives different barrier height, position, and curvature [11–13]. Moreover, this force is a zero-range force and density dependent by nature. This model can be applied for inter-nuclear potential, which consistently considers the saturation property of the nuclear matter and it is known as the EDF. This model assumes that the density of each colliding ion remains the same at all distances during the collision. Using this formalism and various types of Skyrme forces,the earlier studies have shown that this method can account for the elastic scattering and fusion barrier height of16O +16O reaction[14].Brink and Stancu [15] have investigated the applicability of this method using the Skyrme energy functional. They have shown that both the EDF and proximity potential are consistent with each other. The same work has also been performed by Dobrowolski et al. [16] using a higher order Thomas–Fermi approximation(TFA)for the kinetic energy and spin–orbit-densities. Recently, the EDF has been applied to simplify the coupled-channel calculations for heavy-ion nuclear fusion reactions [17–19]. The Skyrme energy density formalism (SEDF) is given as a sum of the spin–orbit-densities dependent universal functions; the universal function parameters are obtained for different Skyrme forces [20]. This method is advantageous in solving the barrier modification problems by introducing the effects of either modifying the Fermi density parameters(the half-density radii and surface thickness for exact SEDF calculations) or constants of the parameterized universal functions, as mentioned in reference [15]. Further,for nuclear systems, the semi-classical extended Thomas–Fermi (ETF) approach is extended at finite temperature[21, 22] and is limited for free energy and entropy density functions only. In the semi-classical formalism, we have included the temperature effects, in the following spin–orbit density J→（ρ） via the nuclear density, taken as the two-parameter Fermi-density function [23]. This follows from the fact that the HF density approximately takes a shape of the Fermi type at higher temperatures;the density becomes flat in the interior region of smaller ‘‘r’’ values.Furthermore, the shell model density distributions, the Fermi density distributions,and the total density interaction potential are approximately the same,at least in the surface region of relevance for the heavy-ion collision. In actual case, the barrier height decreases with increase in temperature. However, there is a vital point of difference in temperature dependence of the two approaches, whereas the order of the barrier remains the same in the semiclassical case.The different filling of the shell model states changes the approach of the same microscopic shell models. Therefore, we have applied the EDF with Skyrme forces SkM*,SLy4 and SLy5 to obtain the fusion reaction cross-sections for the systems that form the same compound nucleus (CN) in the mass region ～200 amu,without adjusting any parameters in the Skyrme forces.The nuclear reactions16O +184W,30Si +170Er, and40Ar +160Gd, which were studied in the present investigations, form the same CN200Pb with different entrance channel mass asymmetry (α). The effect of mass asymmetry on the fusion reaction and the role of incompressibility (K) in nuclear dynamics are discussed in the following sections.The calculated fusion cross-sections are compared with the others experimental values and with cross-section obtained by the coupled-channel CCFULL code [24]. The CCFULL code calculates the fusion crosssection and mean-angular momentum of the CN under the influence of coupling between the relative motion and several nuclear collective motions. Using this formalism,the fusion cross-sections for the above systems in the given energy range well above the barrier were determined.

2 Theoretical background

It is well known that the ion-ion interaction potential can be generated using the SEDF [25]. Using the SEDF, it is possible to understand the fusion of two nuclei at various energies,predict the mass of nuclei as accurate as the semiempirical mass formula,predict the ground state properties of the nuclei, and predict the fission barrier heights for all nuclei available in the periodic table [26]. Generally, in nuclear reactions the total potential is a combination of the nuclear, Coulomb and spin parts. However, in the SEDF,the total potential VT(R) is the combination of the nuclear part VN(R),which is the inclusion of spin–orbit interaction,and the Coulomb part VC(R). This total potential is given as:

In the SEDF, VN(R) between the projectile and target is a function of the distance between the two nuclei. This potential is determined using the Hamiltonian H that depends on the nucleonic density ρ, kinetic energy density τ, and spin density J. It is given by

The half density radii R0iand the surface thickness aiare determined by applying a polynomial fit to the experimentally determined values of the nuclei in the mass range from 4 to 238 amu [22, 35].

3 Result and discussions

Heavy ion-induced fusion reaction is a sensitive tool to probe the shape,structure,and size of an atomic nucleus as well as the reaction dynamics of a di-nuclear system(DNS)[35].In the fusion of heavy ions,the relative kinetic energy of an entrance channel converts into the internal excitation energy of the CN and this internal excitation energy is distributed among all the nucleons in the nucleus. The fusion reactions can be explained based on the energy density distribution of the interacting nucleons in the nuclei. Therefore, in the present work, calculations of the SEDF were carried out using energy density distributions.Systems, such as16O +184W,30Si +170Er, and40Ar +160Gd were used, which form the same CN,200Pb.The ion-ion potential parameters are determined using compatible Skyrme forces like SkM*, SLy4, and SLy5. It is important to notice that in the present investigations,the reactions with different entrance channels and α were selected deliberately to form the same CN. The α are different with respect to the Businaro–Gallone mass asymmetry (αBG) [36]. Some fitting parameters are required for the corresponding Skyrme forces to calculate the ion-ion potential parameters using the HFB method. Theseparameters are tabulated in Table 1 with their respective forces. The Woods–Saxon potential parameters, calculated using the Akyuz–Winther (AW) formalism, along with α and the deformation parameters for the corresponding systems are given in Table 2. The local ρ, τ, and J density distributions of the nuclei for all the above reactions were determined using the HFB program. A typical local densities distribution of16O +184W for both neutron and proton are shown in Figs. 1 and 2. The Skyrme energy density function H(r→）， as given in Eq. (8), was evaluated using local densities, which are obtained from the Skyrme forces of the HFB program. The interaction nuclear potential VN(R), as given in Eq. (4), was determined using this H( r→）. The nuclear potential for all the Skyrme forces for the selected reaction systems is shown in Fig. 3.In this figure,we notice that the depth of the potential depends on the K of nuclear matter and the entrance channel α of the reaction; K is a significant component of the equation of state(EOS)of nuclear matter and it is one of the interesting subjects in the study of heavy-ion fusion reactions. For the investigation of the fusion process,different K values were used, which result from the corresponding effective interactions [37, 38]. The results obtained in our calculations show that the theoretical values are sensitive to the values of K.Therefore,it is very interesting to describe the nuclearfusion reaction using different effective interactions with different K and α values. Consequently, by knowing the K value, we can understand the variations in incompressibility of nuclear matter for various energies of projectile.

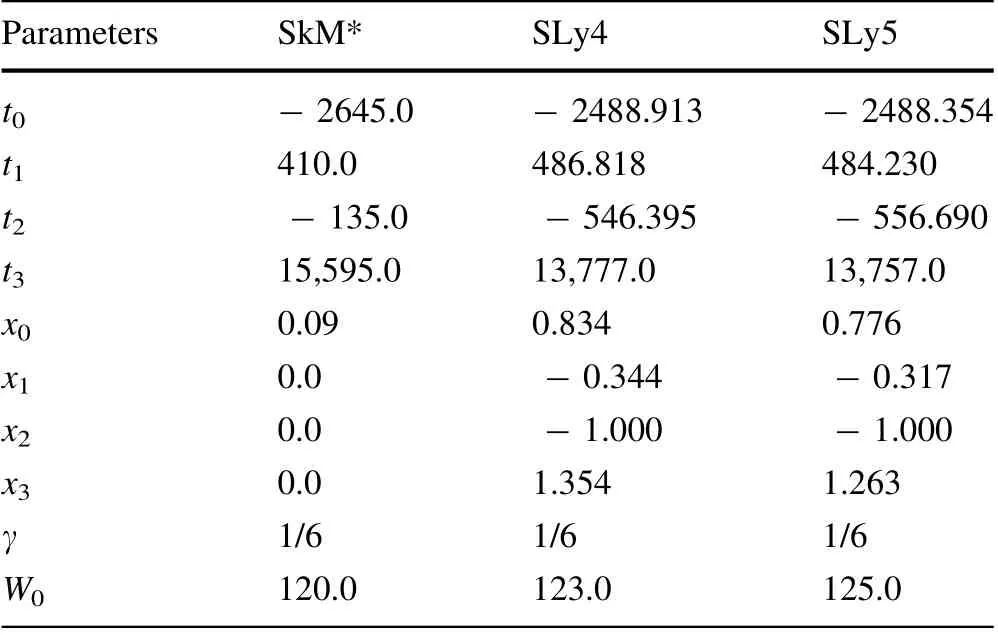
Table 1 Fitting parameters for the different Skyrme forces used in the SEDF

Table 2 The parameters α, β2, and the potential parameters calculated using the AW formalism for the corresponding systems

For the calculation of EDF based on each Skyrme force,we have estimated the Fermi density distributions using the parameters obtained from the fitting results of the HFB.The calculated density distributions’ diffuseness parameters of the nucleons for the projectiles and targets of the systems16O +184W,30Si +170Er, and40Ar +160Gd are shown in Figs. 1 and 2 using Skyrme forces SkM*, SLy4 and SLy5. The interaction potentials were obtained for above mentioned reactions using the calculated densities with the respective Skyrmes.The properties of a calculated fusion barrier potential, viz. V0, a0, and RB, are given in Table 3 for the corresponding Skyrmes.The results clearly indicate that V0increases with the increasing K value. In other words, the increase in the value of K increases the depth of reaction potential pocket. This observed increase in the potential depth may be due to a vital role of theperipheral nucleons in the heavy-ion reaction. Another set of potential parameters for the above systems was calculated using the AW formalism for the CCFULL calculation(Table 2) [39]. It is also to be noted that the system16O +184W has α ＞αBG,and the systems30Si +170Er and40Ar +160Gd have α ＜αBG. In case of incompressibility,SkM*[40]has lesser incompressibility as compared to SLy4 and SLy5 [41]. The nuclear potential parameters obtained from different Skyrme forces and with different incompressibility of the HFB are given in Table 3. The Coulomb part of the nuclear reaction was also estimated using Eq. (9)for all the systems.The total potential for the three Skyrme forces were determined for all the selected systems using the nuclear and coulomb potentials. There exists a potential pocket that is responsible for the capture of the nuclei. The deformation of the interacting nuclei is neglected here to avoid the long duration of the calculation[42, 43]. With respect to the α, the system40Ar +160Gd may have less capture probability; therefore, the fission barrier height appears to be very less compared to the remaining systems, and hence, the contribution of the quasi-fission may lead to less fusion probability. To confirm this, our group is planning to experimentally measure these type of systems in the above mentioned energy range using a recoil mass separator. By incorporating these potential parameters—derived from the different Skyrme forces—in the CCFULL code as an input, we have calculated the fusion cross-section for reactions16O +184W,30Si +170Er, and40Ar +160Gd. The fusion cross-sections of the CN are calculated using the following equation:

Table 3 Calculated potential parameters using the Skyrme forces

where Pl（E）is the transmission probability or penetrability for the l-wave scattering and k is the local wave number for the lth partial wave [24]. It has been used to explain the fusion cross-section in CCFULL at energies near and above the barrier [39]. The theoretical fusion cross-section at various excitation energies have been compared with the available experimental values [44, 45] and the theoretical fusion cross-sections obtained by the CCFULL code with Woods–Saxon potential parameters of the AW formalism as the inputs. Figure 4 gives the comparison of fusion cross-sections. As shown in this figure, the density distributions of the heavy ions, which were calculated by different methods and using different parameters of Skyrmes,influence the fusion barrier,which are calculated using the EDF. With this motivation, we have carried out a comparative study of the fusion barrier using SkM*,SLy4,and SLy5 forces, in addition to the Fermi density distribution including the parameters determined in the SEDF. The total fusion cross-sections were computed from the estimated potentials and compared with the available experimental data.By varying the K values with different α of the same CN, a good agreement was obtained between the calculated fusion cross-sections derived from different Skyrme forces and the available experimental fusion crosssections at different bombarding energies. It was also observed that as the K value increases, the depth of the reaction capture pocket increases. In other words, it increases the probability of the fusion and level density.Similarly, with the increase in α, the fusion probability would also increase.It implies that α between the projectile and the target nuclei is responsible for the deformation of the DNS during the dynamic process.If α value is large,the DNS will be less deformed and consequently, the contribution of the fission and fission-like probabilities will be less.Conversely,if α value is small,the DNS will be more deformed, and therefore, the contribution of the fission or fission-like probability will be more. Further, K also depends on the nucleons lying on the surface or on the periphery of the nuclei, which are more actively involved during the interaction, even though the system is less asymmetric. In other words, K would enhance the probability of the capture cross-section even for less asymmetric systems.

4 Conclusion

In the present investigations, different Skyrme forces were used to estimate the fusion cross-sections at energies well above the Coulomb barrier for the reactions16O + 184 W,30Si +170Er, and40Ar +160Gd. In this study, three systems were selected such that the first reaction has α ≥αBG,the second one has α＜αBG,and the third one has α ＜＜αBG. The results of the SEDF calculations show that the calculated values are in close agreement with the experimental values of16O +184W system,indicating that whenever α is close to αBGthe fusion crosssection values,based on Skyrme forces,closely agree with the experimental values. On the other hand, in the case of30Si +170Er (α＜αBG),the calculated fusion cross-section based on Skyrme forces were found to be higher than the experimental values. It is interesting to note that as the energy increases the deviation between the theoretical and experimental values decreases. In the case of40Ar +160Gd, there are no experimental data on fusion cross-sections.Therefore,we have compared the calculated fusion cross-sections based on Skyrme forces with the values obtained from the CCFULL code. Interestingly, the calculated theoretical values closely agree with the experimental values in the higher energy region,but in the lower energy region,the values predicted by CCFULL are higher than the theoretical values. Therefore, we may conclude that the fusion cross-section values,obtained with different Skyrme forces, can be used not only to estimate the fusion cross-section for any projectile and target combination,but it can also throw light on the effect of entrance channel α on the fusion cross-section. Further, there is no need to change the parameters of Skyrme force to modify the barrier as the theoretical framework based on the Skyrme forces can reproduce the corresponding experiment values.For the fusion cross-sections at sub-barrier energies, different Skyrme forces are required for the different reactions to reproduce the experimental data.A single Skyrme force cannot reproduce the fusion cross-sections over the entire energy range for the selected reactions.