基于电流型CMOS电路的四类三变量函数的新型算法及实现
姚茂群,孙 曦
(杭州师范大学信息科学与工程学院,浙江 杭州 311121)
0 引言
如今集成电路的功耗问题成了研究的一个重大难题,而电流型电路能很好地解决这一问题[1].电流型电路能够在较低的电源电压下工作,并且功率不会随着工作频率的提高发生太大的变化[2].同时,CMOS电路具有较低的静态功耗,且允许较宽的电源电压范围.因此,国内外对电流型CMOS电路一直保持着极大的关注[3].
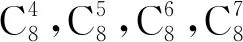
1 阈算术代数系统
1.1 阈算术代数系统的定义
阈算术代数系统即以非负运算(这里我们不做讨论) 、算术运算及阈算术运算为基本运算构成的代数系统.而阈算术函数就是其逻辑关系的解析,其值为一切自然数.在阈算术函数中, “·” 表示算术乘法运算,“+”则表示算术加法运算,表示乘法的点符也可以省略.
1.2 基本运算及性质
第一,阈算术代数系统提出了一个完备运算集,在该完备运算集中定义了信号变量x,y,z∈(1,2,3…,m),阈值t,t1,t2∈(0.5,1.5,…,m-0.5),并且m为大于或等于零的整数.
第二,在联结运算的基础上,更进一步地提出了阈算术运算,其主要内容如下[5]:
1)高阈算术运算:
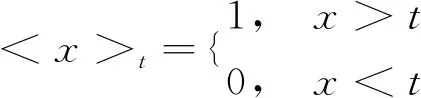
(1)
2)低阈算术运算:
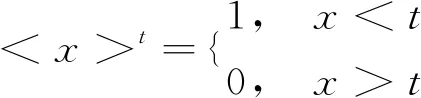
(2)
3)双阈算术运算:

(3)
1.3 阈算术函数的算术乘法运算和算术加法运算
1)算术乘法运算:〈x〉t1·〈y〉t2
乘法运算可以通过串联运算得到.如图1所示:

图1 算术乘法运算Fig.1 Arithmetic multiplication图2 算术加法运算Fig.2 Arithmetic addition
输出f即为〈x〉t1·〈y〉t2.
2)算术加法运算:〈x〉t1+〈y〉t2
加法运算可以通过并联运算得到.如图2所示.输出f即为〈x〉t1+〈y〉t2.
1.4 阈算术函数的性质
根据阈算术函数的定义,可得到如下性质:

(4)
1.5 和图
在阈算术代数系统中,有着与K图(卡诺图)类似的图形表示——和图.和图的坐标排列与K图的坐标排列是完全一样的,左上方的斜线两边分别对应于变量的值,方格内的值对应于阈算术函数值的大小.在K图中,所有值都是不大于1的,但是在和图中,阈算术函数的取值范围为所有自然数,也就是说,从函数值域上看,阈算术函数是包含逻辑函数的.
为了方便与逻辑函数的K图对应,将和图的结构设计成与K图基本相同,阈算术函数的函数值填入对应的和图的方格内.总结K图和和图的区别如下:
1)和图:小格内的值可以是除0和1外的其他自然数;
2)K图:小格内的值必须是0或者1.
图3所示为三变量二值阈算术函数F(x1,x2,x3)的和图.用和图来表示阈算术函数有以下三大优点:
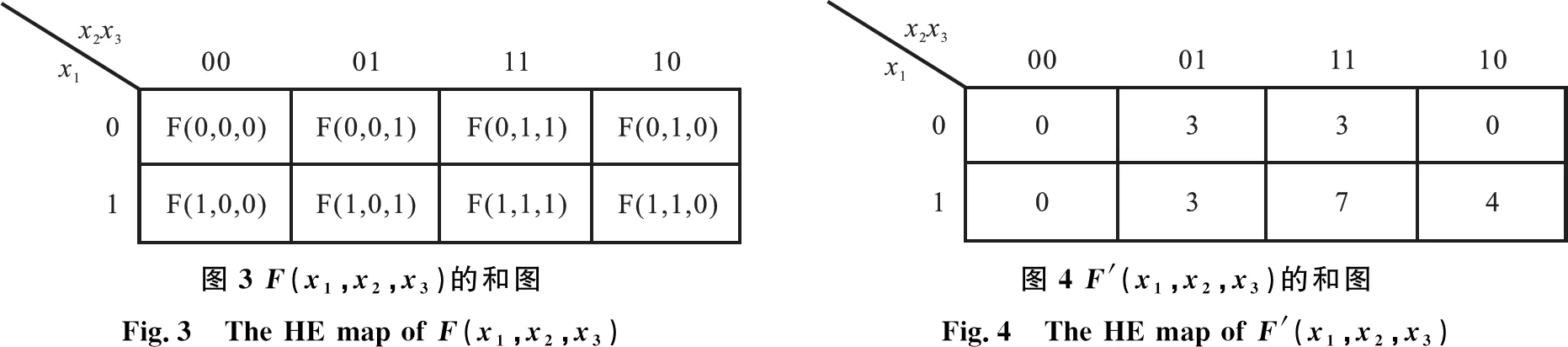
图3 F(x1,x2,x3)的和图Fig.3 The HE map of F(x1,x2,x3)图4 F'(x1,x2,x3)的和图Fig.4 The HE map of F'(x1,x2,x3)
1)能够化简复杂的阈算术函数的函数式(一般来说,很难直接对阈算术函数进行化简);
2)和图的表示使阈算术函数的特点更加清晰,即使不同阈算术函数式的形式差别很大,只要和图相同,那么它们也是等价的;
3) 阈算术函数相互间的运算可以由对应的和图得到,图形化的表示方法能够使运算过程变得直观和简单.以二值三变量阈算术函数F′(x1,x2,x3)=4x1x2+3x3为例,根据函数表达式,便可得到相应的和图[6],如图4所示.
2 基于电流型CMOS的三变量函数分类方法以及和图转化
2.1 电流型CMOS的三变量函数分类方法
前面已经研究过,根据非门的数量将这8个最小项分类,能获得最简单、最易于实现的分类方法非门数量分类法.因此可以得到4类,这里我们将其称为“0”类,“1”类,“2”类,“3”类.
“0”类对应的是最小项ABC;
根据这4类最小项,我们可以得到对应的和图表示,如图5.

图5 非门数量分类和图Fig.5 The HE map of NOT gates’ classification
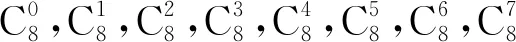
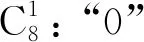
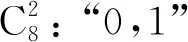
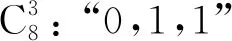
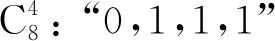
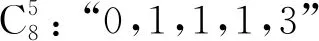
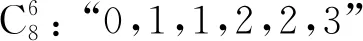

2.2 和图转化法
在“1”类和“2”类中,这些最小项都是相似的.此前我们的研究已经提出了一种新的方法,它的名称为“和图转化方法”,可以使阈值算术代数与和图之间的转换更加容易.


图6 “0,1”类函数Fig.6 The function of “0,1” class
那么另外两种“0,1”类我们可以通过直接和图转化法得到,即通过交换A,B,C 3个变量的位置得到.具体如图7,图8,图9:

图7 A和B交换Fig.7 Switch A and B图8 B和C交换Fig.8 Switch B and C图9 A和C交换Fig.9 Switch A and C图10 另一种“0,1”类函数Fig.10 Another function of“0,1”class
例如:倘若我们想得“0,1”类中的另一个函数的和图,如图10,只需要将〈A+3B+2C〉4.5中的A和C交换,得到〈2A+3B+C〉4.5.
3 基于电流型CMOS电路的四类三变量函数的新型算法
3.1 新型算法的提出


3.2 算法步骤

图11 F'1(A,B,C)的电路图Fig.11 Circuit of F'1(A,B,C)图12 F'2(A,B,C)的电路图Fig.12 Circuit of F'2(A,B,C)
采用TSMC180 nm工艺参数对电路进行Hspice模拟,对应于逻辑值0的电流为0,对应于逻辑值1的电流为10 μA,这里vdd均采用1.8 V,模拟得到的电路瞬态特性如图13所示,模拟结果表明,所设计电路具有正确的逻辑功能.
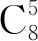
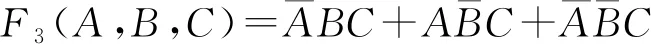

图13 瞬态特性(1)Fig.13 Transient response图14 瞬态特性(2)Fig.14 Transient response
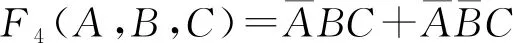
通过模拟验证可得瞬态特性图如图16所示.
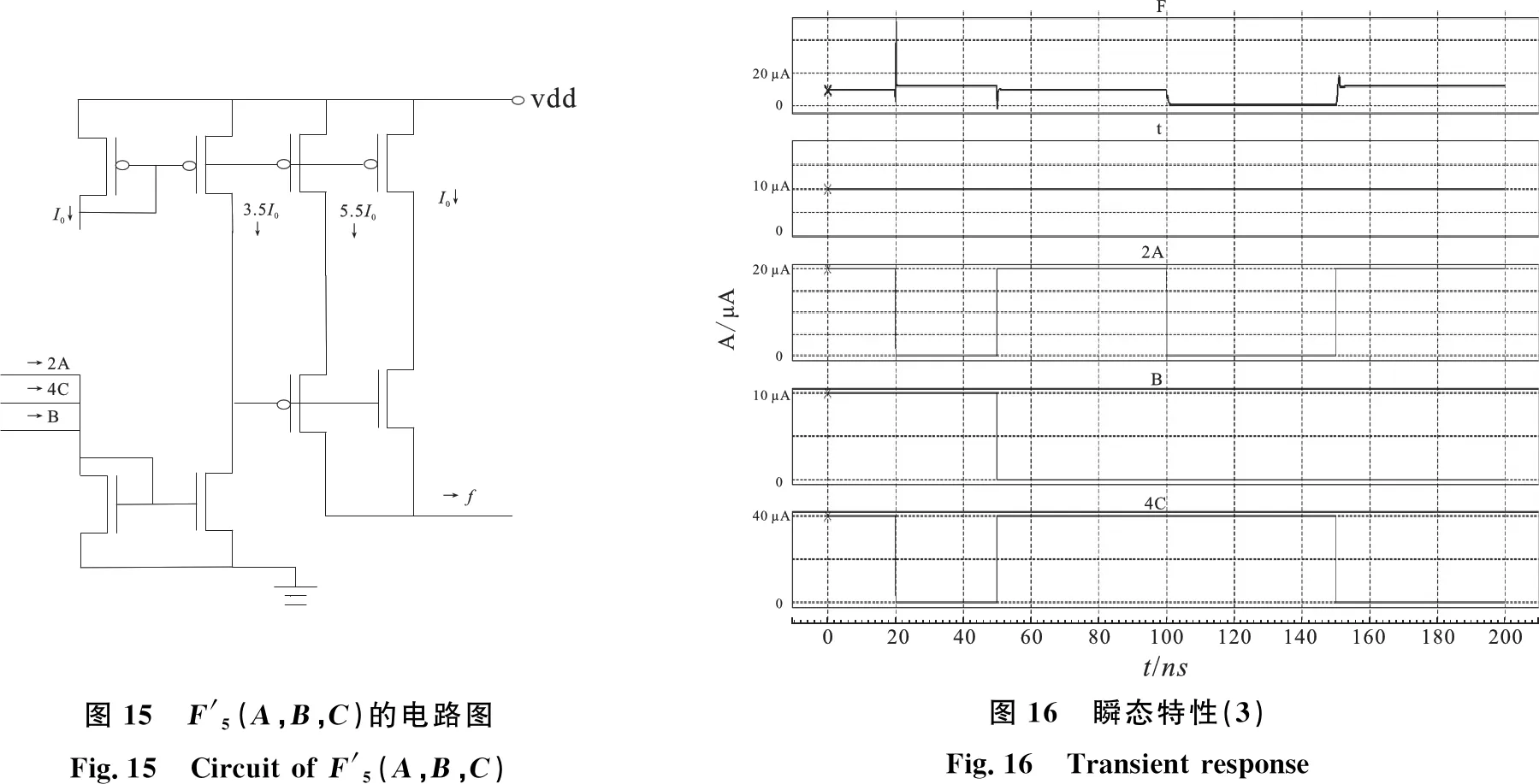
图15 F'5(A,B,C)的电路图Fig.15 Circuit of F'5(A,B,C)图16 瞬态特性(3)Fig.16 Transient response
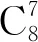
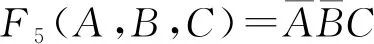
通过模拟验证可得瞬态特性图如图18所示.
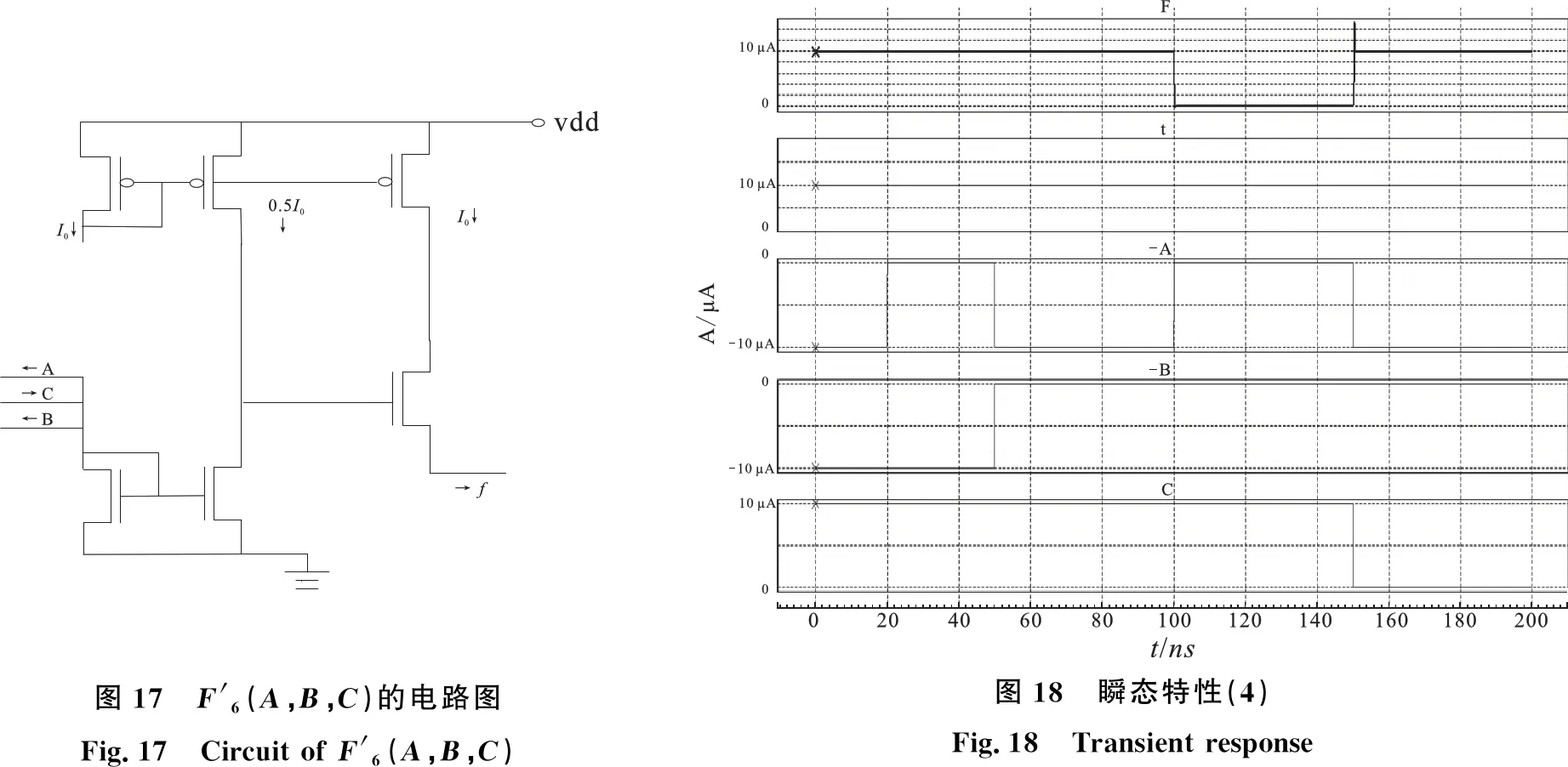
图17 F'6(A,B,C)的电路图Fig.17 Circuit of F'6(A,B,C)图18 瞬态特性(4)Fig.18 Transient response
到此,我们已经把所有的三变量函数对应的电流型CMOS电路全部实现完成.
总结该算法的步骤:

3)根据阈算术函数画出对应电路图.
4)通过Hspice软件模拟验证.
4 总结

但是,目前只是通过电流型CMOS电路实现了所有的二值三变量函数,还可以进一步研究三值三变量函数,四值三变量函数等,然后拓展到n变量函数,使得这个算法变得更加通用[8-12].

