考虑地震风险下的铁路走向方案决策方法研究

曹 祥

（中国铁路设计集团有限公司，天津 300301）

我国地处亚欧板块与太平洋板块的交界地带，历史上曾多次发生重大地震。尤其是我国西南山区震裂带大量分布，更是地震频发。重大地震一旦发生，就会对铁路线路产生广泛而深远的破坏。而我国《中长期铁路网规划》中，明确未来我国“八纵八横”高铁网络中有一半以上线路将不得不经过地震艰险山区[1]。如此形势之下，如何在地震风险下选择一条前期建设和后期运营风险综合效益最佳的线路，将是设计人员和决策者未来要面对的巨大挑战。

近年来因汶川地震的巨大破坏力和后续影响，我国许多学者也开始广泛关注与研究地震山区铁路选线决策问题，并取得了一些学术成果：朱颖等[2]依据断裂构造地貌理论与地震波动理论探讨了方案走向与空间定线的技术与原则；罗圆等[3]针对川藏铁路提出利用ALARP准则对地震风险进行分类，并依据分类结果给出了方案风险调控程式。陈蓉淮[4]利用RS和GIS技术对地震山区铁路灾害进行综合评估，可用于指导选线决策。通过分析学者的研究成果可见，目前学者主要从提高空间选线减灾技术和首先单独判断地震风险的可容忍度再对方案进行风险调控两个层面指导选线决策[2-6]，将地震风险纳入铁路选线前后期进行综合决策评价的研究还相对较少。

为此，文章以力求贴近决策者实际的决策模式为切入点，构建了基于前景理论的铁路选线决策模型，将不同地震风险状态纳入决策模型中对方案进行综合评价。因为前景理论所得结果容易受到决策者主观情感的影响，一些极端指标值可能会决定最终方案的合理性，而VIKOR法能够中和各指标之间的不相容度，从而得到总体最优妥协解[7]，避免了前景理论的不足。所以文章将前景理论与VIKOR相结合，提出了一种考虑地震风险的铁路方案优选决策方法用以指导铁路选线，以提高地震山区铁路选线质量和水平。

1 云模型

云模型是一种反映现实生活不确定关系的数学理论，其核心是利用期望Ex、熵En和超熵He三个数字特征来表示定性概念。其中，期望Ex表示定性概念的平均水平；熵En反映了定性概念的模糊性；超熵He用来度量云滴的离散程度和确定度，反映了定性概念的随机性。因此，云模型综合地考虑了定性概念自身的随机性和人们对定性语言的模糊认知。相关定义[8]如下：

定义1：设U={x}为一论域，C为可表示定性概念的语言值，若元素x对定性概念C的隶属度μC（x）是一个具有稳定倾向的随机数，则称这种隶属度μC（x）在论域U上的分布为云，即μC（x）：U→[0,1]，均有x→μC（x）。通常把云模型记为C（Ex,En,He）。

定 义2：设C1（Ex1,En1,He1）和C2（Ex2,En2,He2）为论域U中两朵一维正态云，根据正态云“3En规则”，正态云C1和C2的Hamming距离为

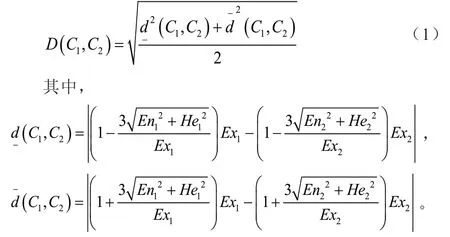
为了使两朵云C1、C2能够比较大小，文章引入云模型可能度的概念[9]。论域U中的正理想云为，则P（C1≥C2）为C1≥C2的可能度，计算公式为

其中，D（C+,C1）和D（C+,C2）分别为C1和C2与理想云C+的Hamming距离。若P（C1≥C2）≥0.5，则C1≥C2，否则C1＜C2。特别指出，若P（C1≥C2）=P（C2≥C1）= 0.5，则云C1=C2。

2 前景理论

前景理论是由Kahneman等学者提出的一种较新的决策理论。它考虑了决策信息的不确定性与决策者自身心理特征在决策过程中的作用，因此更贴近决策者实际的决策行为[10]。前景理论通过方案综合前景价值V的大小实现各方案排序。而前景价值V由价值函数v和决策权重函数π两部分共同决定。具体计算公式如下：

其中，价值函数v（x）表示决策者对各项方案属性心理上的主观感受价值。决策权重函数π（P）表示决策者对客观世界外部状态的主观感知概率。二者的计算公式如下：

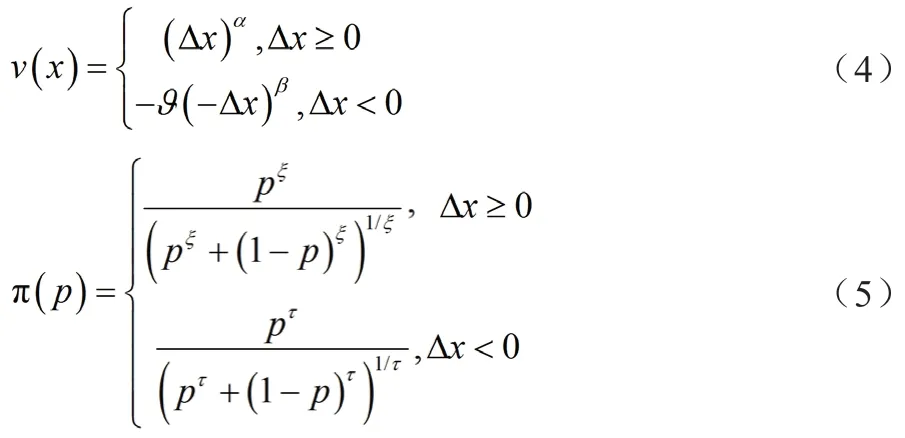
式中：△x为各项方案指标值偏离参考点的距离，表示获得收益，△x≥0表示遭受损失；α、β分别表示决策者心理上对收益和损失的敏感程度；＞1解释了现实生活中往往对损失更厌恶的心理特征；P为外部环境状态的客观概率；ξ和ι分别为决策者偏好收益与规避风险的心理对外部客观概率形成主观决策权重过程中的影响系数。经许多学者研究后，相关参数通常取值为α=β=0.88，=2.25，ξ=0.61，ι=0.69。

3 构建地震风险下铁路走向方案决策指标体系

地震山区铁路走向方案优选是一个涉及多因素的复杂性、不确定性、多目标决策问题，需要综合考虑地形地质地物、土建投资、环境、后期运营、经济据点、矿藏分布、路网布局等多项因素。文章通过提炼前人的研究成果，以科学、全面、符合实际为原则，从技术、经济、施工难度、地形地质条件、社会效益五个维度出发，构建了涵盖技术可行性、经济合理性、施工条件及环境影响、社会政治经济意义四个决策指标准则层，见图1。

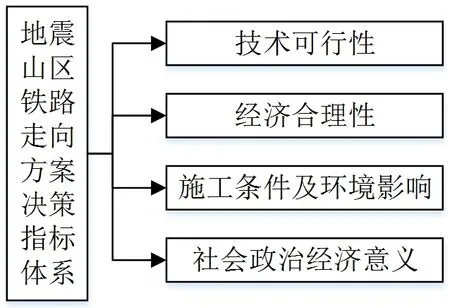
图1 地震山区铁路走向方案决策指标体系

为了全面反映地震山区铁路选线因素的影响，以提高线路决策结果的有效性，需对每项指标层涉及的主要因素进行界定。值得注意的是，地震山区的地震因素影响突出，因此决策过程中除了考虑非地震山区一般铁路选线影响因素，还需考虑地震因素对各类决策指标层的影响。技术可行性指标层主要考虑线路长度、桥隧总长、征地拆迁量、土石方量、地质条件、地震动峰值加速度、地震因素对线路各类构造物设计标准的影响以及各类抗震措施的设置技术等因素；经济合理性指标层主要考虑工程投资、运营费用、机车购置费用、后期地震因素造成的线路各类构造物的震害损失以及运营中断导致的运营收益损失、地震因素导致的后期修缮维修费用等因素；施工条件及环境影响指标层主要考虑地形地质条件以及抗震设计带来的施工难度、工程建设与地震因素的相互作用对生态环境造成的影响等因素；社会政治经济意义指标层主要考虑线路带动周边地区经济发展与满足地方需求的能力、改善路网与城市规划布局方面的积极意义、后期地震因素导致线路中断运营带来的社会政治经济方面的影响、地震因素对社会各方对线路应急救援管理难度的影响等因素。

4 基于前景理论和云模型的铁路线路方案决策方法

4.1 问题描述

在地震山区铁路线路优选方法问题中，假定有待选的铁路线路方案集A=｛A1,A2,…,Am｝，其中Ai表示第i个铁路线路方案；线路方案的决策指标集合为U=｛U1,U2,…,Un｝，其中uj表示第j个指标；x=（x1,x2,…,xk）为铁路线路行经区域未来一定时期内可能发生的地震等级类型，其中xt表示第t种地震状态；ω=（ω1,ω2,…,ωj）表示对应决策指标的权重，其中ωj表示决策指标Cj的权重，显然应满足0≤ωj≤1，；S=｛VG,G,SG,F,SP,P,VP｝=｛很好，好，较好，一般，较差，差，很差｝为决策者对线路方案指标的不确定语言评价集。

为综合反映定性概念自身的随机性和人们对定性语言的模糊认知，利用云模型将不确定语言评价值定量化。文章引用文献中云模型与不确定语言评价集的转化关系见表1。

表1 云模型与定性语言评价值的转化关系

因此文章研究的主要问题是决策者分别对各种地震状态下各线路方案决策指标做出评价，选取适当参考点，并确定决策指标权重，最后利用前景理论和VIKOR方法选出最优线路走向方案。

4.2 确定参考点

参考点是决策者心理上判断收益和损失的潜在基准，并与决策者自身的从业经验、性格偏好等因素有关。为了分担每个决策者单一参考点下选择不当的风险，尽可能综合多名决策者信息，文章构建不同地震状态xt下的正理想方案云、负理想方案云、平均期望方案云三个参考点。

正理想方案云：

负理想方案云：

平均期望云方案云：

4.3 确定价值函数

4.4 确定决策权重

决策者的决策权重与决策者的风险态度和地震发生状态的客观概率有关。为了综合考虑地震活动的周期性和随机性，文章引入布朗（BPT）-泊松（poi）联合概率模型[3]对地震状态xt发生的客观概率进行预测。计算公式如下：

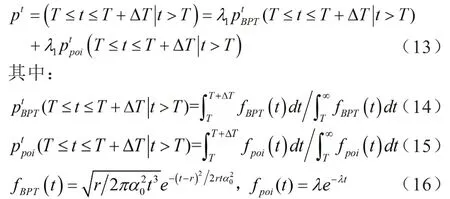
式中：Pt表示地震状态xt发生的概率；r为断裂带的平均复发间隔；λ表示破裂的年发生率，λ=1/r；α0是变异系数，通常取值为0.5；T表示最近一次地震状态xt发生到目前的时间；△T表示新建铁路的服务期，本文取值为△T=100年。λ1、λ2表示地震活动周期性和随机性的组合系数，若地震活动周期性和随机性无明显差异，可取λ1=λ2=0.5。

通过上述确定地震状态xt发生的客观概率Pt后，采用式（5）即可确定地震状态xt下各线路走向方案的决策权重πt（p）。

4.5 确定三参照点下各决策指标的综合前景价值

依据前景理论，可分别计算基于第h个参考点方案在地震状态xt下线路走向方案Ai对应的决策指标uj的前景云价值。计算公式如下：

文章通过设计问卷、专家咨询等手段对相关单位决策群体中潜在参考点的分布情况做深入调查，分别确定决策群体中正理想方案云、负理想方案云、平均期望方案云三个参考点的偏好权重，满足。并通过参考点偏好权重对进行集结，确定基于三参照点在地震状态xt下线路走向方案Ai决策指标uj的综合前景云价值。计算公式如下：

4.6 基于前景理论的综合决策优选方法

铁路线路走向方案决策是一个涉及设计院、政府、相关铁路单位等多方部门共同协商的决策过程。各方代表自己的意见通常有不同的决策准则，而VIKOR方法正是一种用于解决多准则问题的妥协排序决策方法[14]。它的基本原理是通过各决策准则让步而获得离理想解最近的妥协解。因此，文章通过引入VIKOR方法与前景理论相结合对线路走向方案进行决策排序。具体决策步骤如下：

（1）首先确定各决策指标的重要度，即指标权重ω=（ω1,ω2,…,ωj）。为充分吸收决策者的主观经验同时兼顾决策数据本身的信息，文章在决策者主观给出部分指标权重信息的基础上，依据离差最大化方法[15]构建一种线性规划优化模型，即

其中，H为由决策者主观给出的部分决策指标权重信息。利用Matlab或者Lingo编程求解模型可获得决策指标最优权重向量ω=（ω1,ω2,…,ωj）。

（2）确定各线路走向方案综合前景云价值的正理想解f+和负理想解f-。通过4.2～4.5可得到地震状态xt下线路走向方案Ai决策指标uj的综合前景云价值。在此基础上分别定义f+、f-如下：

（3）确定各线路走向方案的群体效益值Si和个体遗憾度Ri，其中i=1,2,···,m。

（4）确定各线路走向方案的折中排序值Qi。其中i=1,2,···,m。

其中，ε∈[0,1]是决策妥协系数，文章取ε=0.5，表示决策结果由各方共同协商确定。

（5）确定最优方案。首先依据Si、Ri、Qi从小到大对各项线路走向方案进行排序，线路走向方案排序越靠前，则方案越优。若满足以下两个决策准则，则Qi值最小的方案为最优方案。

①可接受优势准则：Q（A2）-Q（A1）≥1/（m-1），其中，A1和A2分别为Q值最小和次最小线路走向方案，m为待选线路走向方案个数。

②可接受稳定准则：A1在所有线路走向方案中Si或Ri最优。

若不满足准则①，则A1,A2,…,AM均为总体妥协最优方案，M由Q（A2）-Q（A1）＜1/（m-1）确定；若不满足准则②，则A1和A2构成妥协最优方案集。

5 案例分析

文章选取地震山区某新建铁路雅安至泸定段线路走向方案优选作为工程实例进行决策研究，验证文章所建模型的科学性与适用性。

该段铁路地形地质条件复杂，构造运动频繁，地震频发，气候条件恶劣，会对雅安及其周边地区造成严重破坏，因此该段线路走向的选择对与铁路建设和后期的运营维护都具有重大意义。经设计院研究主要形成经天全方案A1和经荥经方案A2两个方案。其中，经天全方案A1为最终确定方案。我国目前《铁路工程抗震设计规范》只适应于地震峰值加速度0.4g，相当于地震烈度为9度弱的情况。然而，历史上超标准地震是存在的，如唐山、汶川地震烈度均超过了11度。因此文章结合我国新建线路服务寿命通常为100年，假定线路自完工至未来100年内可能面临三种地震状态：（1）大地震（烈度10度及以上，并造成铁路大范围内严重震害）x1；（2）中小地震（烈度小于10度，震害中等，并可通过加强抗震设计、措施进行防控）x2；（3）不发生地震x3。从技术可行性（C1）、经济合理性（C2）、施工条件及环境影响（C3）、社会政治经济意义（C4）指标层出发，给出决策者针对每个地震状态xt、每个线路走向方案Ai的不确定语言评价值，并依据表1将不确定语言评价值转化为云模型评价值，详见表2。

表2 不同地震状态下各线路走向方案指标的云模型评价信息表

其次，依据表2中各方案指标的云模型评价值和式（6）～式（11）计算三种地震状态下各线路走向方案的参考点方案评价值，结果见表3。

表3 不同地震状态下的参考点方案评价值

然后确定不同参考点下各线路走向方案指标的前景价值。三种地震状态发生的客观概率Pt（P1,P2,P3）。根据文献中的研究，未来地震状态x1时，取平均值r=500年，T=6年；未来地震状态x2时，取平均值r=161年，T=40年。依据模型（10），利用Matlab数值积分计算可求得地震状态x1、x2发生概率的近似值P1=0.1194，P2=0.4592，则地震状态x3的概率P3=1-P1-P2=0.4214。依据不同地震状态的客观概率Pt、表3中不同地震状态下的各参考点方案的评价值和式（3）、式（5）、式（12）、式（18）计算三个参考点下各线路走向方案指标的前景值，计算结果见表4。

接着，依据式（12）对三个参考点下各线路走向方案指标的前景价值进行加权融合，决策群体中各参考点的分布比例情况确定为（0.3,0.3,0.4），得到各线路走向方案指标三个参考点的融合前景值见表5。

随后，依据离差最大化思想，并结合决策者给出的部分指标权重信息，用式（13）构建如下权重优化模型：

利用Matlab编程对模型进行编程求解，得到指标最优权重：ω1=0.15，ω2=0.4，ω3=0.15，ω4=0.3。

最后，依据表5中各方案指标的融合前景值与方案指标最优权重，利用VIKOR方法确定最优线路走向方案。通过式（14）～式（18）得到计算的结果见表6。

根据表6的计算结果，结合VIKOR的最优方案的判定准则，显然有Q1＜Q2且线路走向方案A1同时满足准则①和准则②，因此线路走向中经天全方案A1为最优方案。

在实际决策过程中，决策者对群体效益和个体遗憾可能会有不同的决策态度，进而会影响到决策结果。因此，为了验证最优方案的稳定性，文章将决策妥协系数ε∈[0,1]以0.1为步长进行取值，探讨决策者采取不同决策态度时最优方案的变化情况。计算结果见表7。

表4 不同参考点下各方案指标的前景值计算表

表5 三参考点下各方案指标的融合前景值计算表

表6 各线路走向方案的Si、Ri以及Qi

依据表7中的计算结果与VIKOR的判定准则，可得到决策者采取不同决策态度时线路走向方案的排序情况，见图2。

表7 各线路走向方案的Si、Ri以及不同决策态度ε下的Qi值

图2 不同决策态度下方案排序结果

随着决策妥协系数的变化，决策者从看重个体遗憾逐渐向更多考虑群体效益倾斜，从图2可以看出，最优方案均为A1，说明了最优方案是稳定的。文章所得最优方案与设计院最终确定的方案是一致的，验证了上述决策方法的科学性与可靠性。

6 结论

（1）在地震频发山区进行铁路选线时，如何综合平衡后期地震风险与线路建设的技术、经济及社会效益之间的关系，将是设计人员和决策者面临的难题。为此，文章基于前景理论将未来地震风险纳入线路优选决策模型中，将未来地震风险划分为不同的情景状态，在不同地震状态下对各线路方案进行评价，并依据未来地震状态发生概率、前景理论与VIKOR方法对各方案实现综合优选。这为地震山区铁路选线决策提供了一种新的思路。

（2）决策过程中，利用云模型表示决策者对线路走向方案的评价值，综合了人类思维模式的随机性和模糊性，能良好反映决策者思维和铁路选线决策系统的不确定性；利用前景理论确定线路方案前景价值过程中，综合考虑了决策者对地震状态客观概率的主观感知与对线路方案属性损失或收益的敏感程度，这更贴近决策者实际的决策模式；依据各线路方案属性前景价值利用VIKOR实现综合优选，兼顾了多方部门的群体效益与个体遗憾，使决策结果具有更高的稳定性。

（3）决策模型中利用布朗-泊松联合概率模型预测不同地震风险状态概率，充分考虑了地震活动的随机性与周期性；依据离差最大化思想与专家给出的部分权重信息，利用数学规划确定线路方案指标最优权重，综合考虑了专家经验与各线路方案指标值的差异性，使指标权重更加合理；综合各线路方案属性正理想云、负理想云、平均期望云三参考点进行决策，照顾了不同决策群体的心理特点，避免了特定类型决策者单一参考点下选择不当的风险，提高了决策的科学性。