镶装式机械密封端面变形加速方法的数值研究*

张志慧，马润梅，李双喜，冯瑞鹏，付光卫

(北京化工大学 机电工程学院，北京 100029)

0 引 言

因节约贵重金属材料，简化制造工艺，镶装式机械密封被广泛应用于各种密封场合。镶装式机械密封的动环或静环采用石墨、碳化钨和氧化铝等材料做密封环，采用金属(碳钢、不锈钢、钛等)做密封环座，依靠环和环座线膨胀系数不同，采用过盈联接装配，配合后接触面上将产生互相压紧的装配应力，形成紧固的静配合。当联接承受轴向力或转矩时，配合面上便产生摩擦阻力或摩擦阻力矩以传递外载荷[1]。

某些镶装式机械密封长期处于贮存状态，在此过程中，密封常出现随贮存时间增长而泄漏异常的状况，可能带来严重的安全隐患[2]。镶装式机械密封静环组件端面沿圆周方向会出现马鞍形变形，径向为内高外低。静环组件的变形将引起较大的介质泄漏率，还会影响密封的动力学性能，会给设备安全使用造成隐患，严重制约机械密封的贮存寿命[3-5]。

随着可靠性水平的不断提高，寿命评估面临着一个长寿命高可靠试样的评估课题。如果按照传统的寿命试验技术进行评估，则往往难于在可行的时间内完成。因此，加速试验的研究在可靠性试验工程领域受到了广泛重视[6-7]。而加速试验加速应力一般分为温度应力(低温、高温)、温度循环、随机振动、温度和振动综合应力[8]。

传统方法研究机械密封的端面变形，大部分选择的是自然贮存状态下正常的密封环，对于存在缺陷的密封环研究较少。

为研究存在缺陷的密封环对机械密封端面变形的影响，探究温度循环加速方法加速端面变形的效果，以某一镶装式机械密封静环组件为研究对象，分别建立正常和存在偏心缺陷的静环组件有限元模型，在自然贮存和温度循环两种条件下，分析正常和存在缺陷的静环组件端面变形规律以及加速方法的效果，为相关密封贮存变形理论和试验研究提供参考。

1 镶装式机械密封结构及偏心缺陷

镶装式机械密封由动环座、动环、静环、静环座、弹簧和壳体等组成，如图1所示。

图1 镶装式机械密封结构示意图

图1中，静环材料为石墨，静环座材料为S30408不锈钢，静环和静环座通过过盈配合联接，共同组成静环组件。

静环组件可能存在的缺陷有：静环底面和静环座出现空隙、过盈量不同、静环内外圆偏心、静环材质不均等。

因偏心缺陷易于实现，可建立该缺陷模型，进行有限元分析。其中，静环组件的偏心缺陷是以外径为基准，内径轴线沿径向偏移一定距离，偏心设定为0.10 mm、0.20 mm、0.30 mm 3种。

2 自然贮存过程有限元分析

涡轮泵机械密封装配完成后，经过长期自然贮存后，静环端面易发生变形现象。李莹等人[9]认为端面变形是由静环座的室温蠕变造成的。分析金属材料的蠕变过程，广泛采用的是Bailey-Norton方程，它能模拟蠕变过程的第一阶段和第二阶段，如下所示：

εcr=Aσntm

(1)

式中：εcr—蠕变应变；σ—应力；t—时间；A—与温度相关的材料常数；n—Norton应力指数；m—小于1的常数。

目前关于S30408不锈钢室温蠕变方程参数拟合的文献较少，笔者采用与其相近的材料拟合参数。韩宁宁[10]根据316L不锈钢室温拉伸试验数据，拟合出A=3.375 27×10-9，n=3.344 25，m=0.140 35，则S30408不锈钢近似蠕变方程如下：

εcr=3.375 27×10-9σ3.344 25t0.140 35

(2)

ANSYS Workbench软件的Bailey-Norton模型如下：

(3)

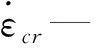
2.1 数值模型

在整个周向上，具有偏心缺陷的静环不具有轴对称结构，但沿过轴线某一平面具有对称结构，故须建立1/2静环组件三维有限元模型。正常静环组件有限元模型与其相似，但不具有偏心。

2.2 材料参数

静环的材料是石墨，静环座的材料是S30408不锈钢。石墨、S30408不锈钢材料各项物理参数如表1所示。

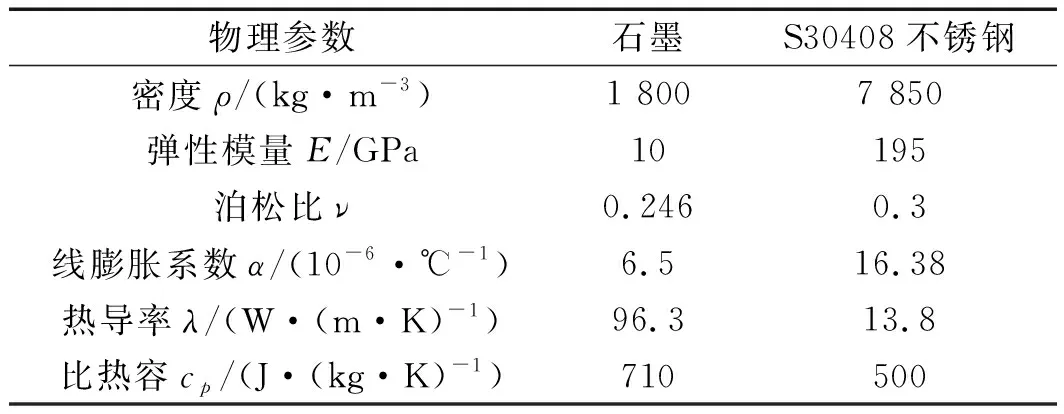
表1 材料物理参数

2.3 接触设置

静环和静环座之间为过盈配合联接，过盈配合的过盈量是基于几何尺寸的概念，ANSYS Workbench设置过盈量有两种方式：

(1)几何尺寸过盈，即在建模过程中考虑实际过盈量；

(2)施加过盈偏移量，即在有限元模型接触方式中设置偏移量，不考虑建模过盈量[11-13]。

笔者采用方式(2)建立静环和静环座之间的过盈配合联接，在ANSYS Workbench中选择非对称接触方式，因静环为石墨，刚度小，选择静环外侧配合面为接触表面，静环座内侧配合面为目标表面，接触公式选择增强拉格朗日方法，过盈量设为0.123 mm。

2.4 边界条件及求解设置

静环座底部设为轴向位移约束，打开大变形。求解分为两个载荷步：(1)初始过盈配合的计算，设为100 s；(2)长期贮存静环组件的蠕变变形计算，时间设为贮存年限。

2.5 模拟结果分析

在ANSYS Workbench软件中，输入贮存时间0年、1年、3年、5年，分析正常和不同偏心的静环组件的蠕变变形规律；在静环组件端面上设置路径，分析端面周向和径向变形规律。

路径如图2所示。

图2 静环组件端面路径示意图

图2中，Path1、Path2、Path3为周向路径，Path4、Path5、Path6为径向路径。

经比较发现：Path1、Path2、Path3 3条路径显示的周向变形趋势一致，选择Path3分析静环组件周向变形随时间变化规律；Path4、Path5、Path6 3条路径显示的径向变形趋势也一致，选择Path4分析静环组件径向变形规律。

随自然贮存时间的增加，正常和偏心缺陷的静环组件的端面周向变形的变化规律，如图3所示。

图3 不同静环组件端面周向变形

正常和偏心缺陷的静环组件径向变形的变化规律，如图4所示。

图4 不同静环组件端面径向变形

由图(3，4)可知，随着自然贮存时间的增加，静环组件的蠕变不断累积，导致端面变形增加。

(1)在周向方向，正常静环组件端面呈现出马鞍型变形，并不断增大。而存在偏心缺陷的静环组件端面变形也是马鞍型，由向上凸起变为向下凹陷，峰谷差值大于正常静环组件。所有静环组件峰谷差值有所增加，但增速放缓；

(2)在径向方向，各种静环组件径向变形为斜线型，且随着贮存时间的增加，斜率进一步增大，但增速放缓。

3 温度循环加速过程有限元分析

3.1 前处理设置

温度循环应力会导致金属材料随时间的累积发生变形，因此，在ANSYS Workbench温度循环分析中，需要添加材料的本构模型。金属材料经常采用的本构模型是Anand模型，即一种粘塑性模型。当材料的温度(绝对温度)高于本身熔点的一半时，就必须考虑粘塑性行为。这种材料行为和蠕变类似，但比蠕变复杂[14]。

而304不锈钢温度循环加速过程数值分析的最高温度远低于S30408不锈钢熔点(1 398 ℃ ～1 454 ℃)的一半，因此，此时Anand模型不再适用，研究人员须采用上述蠕变方程，来分析温度循环应力载荷下S30408不锈钢材料的热变形[15-17]。

模拟温度循环加速过程，需要考虑整个时间历程的热应力对静环组件的影响，须选择ANSYS workbench瞬态动力学模块进行热-结构直接耦合分析；要在瞬态动力学模块实现热-结构直接耦合分析，需要插入命令流，修改实体单元和为耦合单元，选用solid226单元，设置接触单元包含位移和温度自由度，设置求解算法。设置载荷步，分别求解初始过盈配合状态、温度循环热应力。瞬态分析需要设置合适的载荷子步，否则得不到收敛解。

为使求解更加精确，笔者输入随温度变化的S30408不锈钢的弹性模量，如表2所示。

表2 S30408不锈钢的弹性模量

随温度变化的S30408不锈钢的线膨胀系数，如表3所示。

表3 S30408不锈钢的线膨胀系数

参考GB/T 2423.22-2012《环境试验 第2部分：试验方法 试验N：温度变化》标准，笔者选择温度循环区间为-20 ℃～60 ℃、-40 ℃～80 ℃、-60 ℃～100 ℃，高低温暴露持续时间为0.5 h，温度变化速率为1 ℃/min,循环次数2次。

3.2 模拟结果分析

正常和偏心缺陷的静环组件端面周向变形，随温度循环区间的变化规律，如图5所示。

正常和偏心缺陷的静环组件端面径向变形，随温度循环区间的变化规律，如图6所示。

图5 不同静环组件端面周向变形

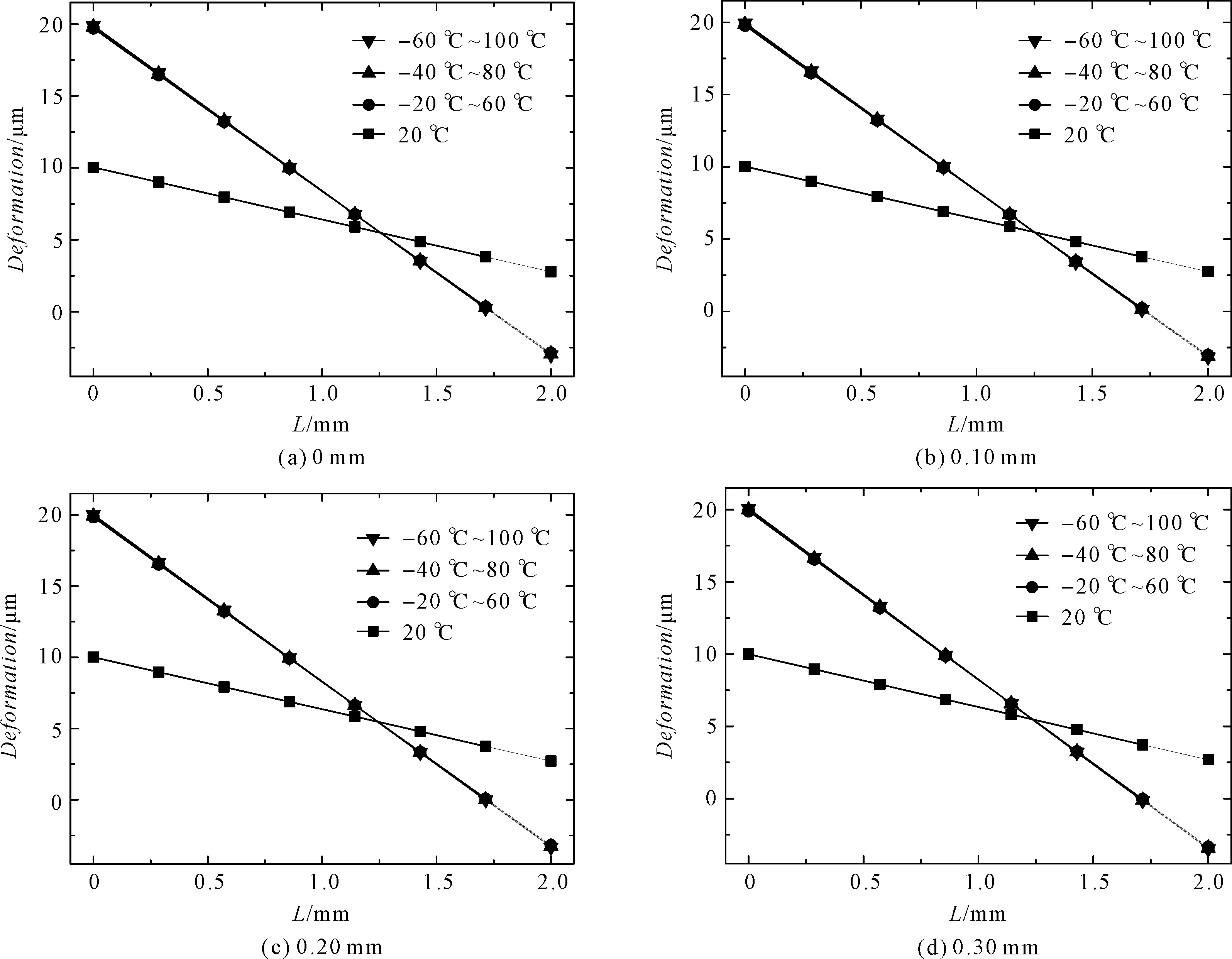
图6 不同静环组件端面径向变形

由图(5，6)可知，随着温度循环区间跨度的增加，加速静环组件的蠕变效果更加明显。

(1)在周向上，正常静环组件端面呈现出马鞍型，向下凹陷，且不断增大。存在偏心的静环组件端面马鞍型由向上凸起变为向下凹陷，也是不断增大。所有静环组件峰谷差值有所增加，且比自然贮存的差值大，但仍然是增速放缓；

(2)在径向上，所有静环组件端面仍然是斜线型，且随着温度循环区间跨度的增加，斜率进一步增大，但增速放缓。

4 结束语

为研究存在缺陷的密封环对机械密封端面变形的影响，探究温度循环加速方法加速端面变形的效果，笔者针对某一镶装式机械密封静环组件，分别建立了正常和存在偏心缺陷的静环组件有限元模型，通过对自然贮存过程、温度循环加速过程进行了有限元分析，结果表明：

(1)各种静环组件沿周向呈现出马鞍型，沿径向呈现出斜线型，且内高外低；

(2)存在偏心缺陷的静环组件端面马鞍型变形比正常的明显，即峰谷差值大于正常静环组件；

(3)随着偏心的增加，静环组件的端面变形有所增加，但峰谷差值变化不大；

(4)温度循环加速过程中，静环组件端面变形有所增加，且比自然贮存的变形要大，说明温度循环加速方法加速效果较好；

上述结论可为机械密封贮存变形的试验研究提供参考。