溜井中矿石压力计算公式分析与讨论
詹森昌
(江西铜业集团有限公司 德兴铜矿,江西 德兴 334224)
1 引言
在有条件利用重力运输的矿山,溜井运输系统是首选方案。它有很多重大优点,但要让其发挥最大效益,必须对一些重大关键问题进行深入研究,掌握其内在规律,以便正确指导生产。溜井井筒装有成千上万吨矿石,是一个非常复杂的体系。矿石产生的压力是怎样分布的,怎样计算的,对井壁磨损破坏有怎样的影响,是人们非常关心的,对设计和生产管理有重要指导意义。
在分析和研究这个很复杂体系时,目前只能从宏观方面、对有关试验、生产中反映出来的现象进行具体的总结、分析和研究,以掌握其内在规律。
2 溜井中矿石压力计算公式
2.1 杨森(Janssen)矿石压力计算公式
它是目前在使用的计算公式。根据“振动放矿”[1]一书介绍,溜井中微分薄层所受的矿石压力如图1所示。
矿石压力平衡方程式:


图1 矿石作用于薄层上的力
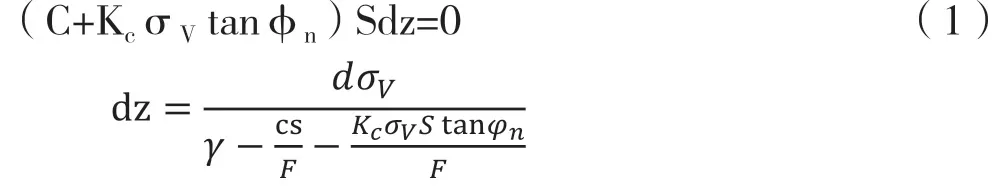
对上式积分得:

式中:σV为微分薄层压力9.8×103Pa;γ为矿石松散体重,t/m3;F为微分薄层面积,m2;S为微分薄层周长,m;KC为侧压系数;C为矿石粘结力,Pa;Z为溜井中矿石高度,m;φn为矿石内摩擦角,度;σh为溜井中矿石侧压力9.8×103Pa;PV为溜井中矿石压力,9.8×103N。
2.2 散体拱形矿石压力计算公式
2.2.1 溜井底部压力试验
金长宇等人对放矿过程中,溜井底部压力变化进行了数字模拟和室内试验[2],其试验过程和结果如下。
(1)数字模拟试验。
计算模型建立高度15m,直径1m的圆形筒仓,圆筒内矿体全部为三角形,其边长0.1m,矿体与矿体之间摩擦角35°,矿体与圆筒内壁摩擦角为5°(原文),每次放矿高度为0.5m。
试验结论:矿体作用在底板上的压力是恒定不变的,其压力值没有跟随高度逐渐降低而出现减小现象。
(2)室内试验。
试验采用直径为40mm、50mm、60mm、70mm、80mm的溜井进行了多次试验。试验物料为砾石,粒径3~5mm,自然安息角为35°,密度1.52g/cm3,砾石与筒壁摩擦系数0.084(原文),装料高度为320mm。为了消除试验的偶然性,各种直径的试验重复测定10次,取平均值。试验结果见表1。

表1 各种不同直径溜井底板压力N
试验结论;观察发现,不同直径下无论放矿高度怎样变化,天平的读数基本保持不变,该结论与数值模拟规律得到了相互验证。
2.2.2 散体拱形压力计算公式
(1)散体物料移动特性。
散体材料结构不同于连续介质材料结构,其沉降变形是在一次次的坍塌过程中完成的,散体材料结构是靠内部一系列拱结构承受、支撑上部压力,而内部结构是自发组织起来,靠颗粒之间摩擦和挤压来维持平衡,当拱结构不能支撑上面的重量时,就很快崩塌,内部开始自组织运动,重组新的拱结构,宏观上表现为沉降[3]。
在放矿过程中,矿岩散体同样出现搭拱现象,通常拱的形成和破坏交替时间短,对移动区的整体来讲,表现出整体移动特征[4]。
矿岩在溜井内的移动是由于具有周期的移动拱的崩塌引起不连续现象的反复[5]。
(2)溜井底板球缺形压力计算公式。
散体物料结构是靠内部一系列拱结构承受、支撑上部压力。也就是说,溜井内矿石自动形成的平衡拱的拱脚未到达井壁时,拱内矿石重量是溜井底板压力。它的形状是一个球缺。当矿石平衡拱的拱脚到达井壁后,拱内矿石重量形成的作用力由拱脚传递给井壁,如图2所示。
球缺中矿石重量Q:
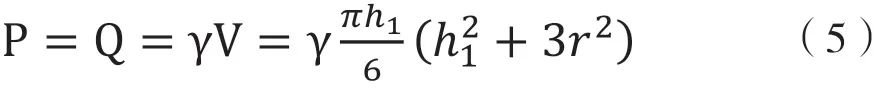
式中P为溜井底板矿石压力,9.8×10-3N;Q为球缺中矿石重量,9.8×10-3N;γ为矿石松散体重,g/cm3;r为溜井半径,cm;V为球缺体积,cm3;h1为球缺高度,cm。
根据表1中溜井底板压力值,用(5)式求出球缺高度h1,见表2。

图2 溜井底板矿石压力

表2 不同直径溜井的球缺高度h1
把h1值进行回归,得出球缺高度与溜井半径的回归方程式:

符号意义同上。
用(6)计算出的球缺高度,反算溜井底板压力值与试验压力值对比,见表3。

表3 试验压力值与(5)式反算的压力值对比N
(3)溜井中矿石的垂直压力和水平压力计算公式。
溜井中矿石重量,除球缺内极小一部分由溜井底板承担,其余矿石产生的重力是以平衡拱的形式,由拱脚传递给井壁,再分解成垂直向下和水平的二个分力。前者与矿石和井壁产生的摩擦阻力相平衡;后者形成对井壁的压力,如图3所示。

由于N力未传到溜井井筒底板,故Fr=N


图3 矿石的垂直与水平压力
式中:T为平衡拱内矿石对井壁的作用力;M为T的水平分力;N为T的垂直分力;α为T的水平夹角;Fr为矿石与井壁的摩擦阻力;β为矿石与井壁的摩擦角。
由图3得:
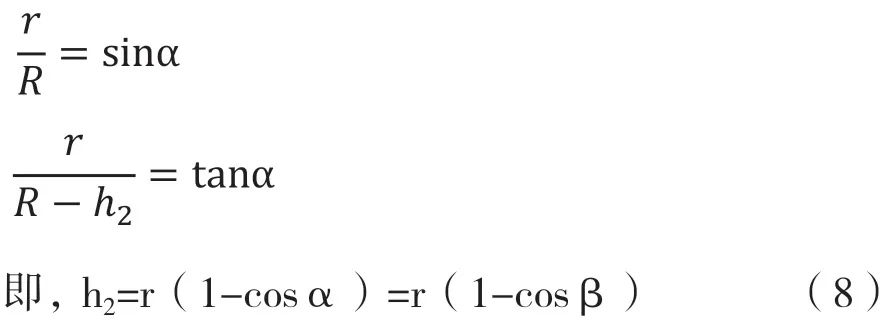
式中:R为矿石平衡拱半径;h2为矿石平衡拱高度;其它同上。
图3,高度为h2的平衡拱ABCD(阴影部分)矿石重量等于高度h2的圆柱体ABCD矿石重量,即:

溜井中矿石作用于井壁的压强PM:

式中:PM为矿石作用井壁的压强;其它同上。
(4)溜井中矿石压力分布示意图。根据上述压力计算公式(5)、(10)、(11)作出溜井中矿石压力与贮矿高度关系的压力分布示意图,见图4。
3 溜井中矿石压力计算与计算公式的讨论
3.1 溜井中矿石压力计算与压力分布
3.1.1 溜井中矿石压力计算公式汇总
以上是介绍了一个在使用的和另一个近来提出的两个不同类型的溜井矿石压力计算公式,其汇总为:

图4 矿石垂直压力分布示意图

图5 矿石水平压力分布示意图
杨森公式:

溜井散体拱形公式:
溜井底板压力计算公式:
溜井中矿石压力计算公式:

式中符号意义同上。
3.1.2 矿石压力计算结果
为了便于比较和讨论,利用上述室内试验数据分别进行计算,设定(12)式中C=0,其计算结果见表4。
3.1.3 矿石压力分布示意图
(1)杨森公式压力分布示意图。根据表4杨森公式的数据,作出溜井中矿石垂直压力变化示意图6。

图6 杨森压力示意图
由于σh=KCσV,故溜井中矿石水平压力变化与图6相似,其大小是KC值倍数。
(2)散体拱形公式压力分布示意图。见图4、图5。
3.2 计算数据对比
3.2.1 溜井底板压力
根据表4,溜井底板压力如表5。

表4 不同直径溜井内矿石压力 N

表5 溜井底板压力N
3.2.2 溜井中矿石垂直压力
从表4和图6曲线看出,杨森公式计算得垂直压力,是随着溜井贮矿高度增加而增大;开始增大很快,后增速减小,最后接近稳定。从表4和图4看出,散体拱形公式计算得垂直压力,除球缺部分外,与贮矿高度无关,只是溜井半径的函数。
3.2.3 溜井中矿石水平侧压力
杨森公式的侧压力σh=KCσV,σV是随贮矿高度而变化的一个函数,故σh也是随着贮矿高度而变化,其变化曲线与图6相似。
当溜井贮矿高度达到一定高度,σV趋于稳定时,二者存在如下关系:

式中:符号意义同上。
3.2.4 二个矿石压力计算公式分析与讨论
(1)杨森公式计算出的溜井底板压力值比试验值大6.2~6.9倍;散体拱形公式计算出的压力值与试验值很接近。
(2)杨森公式计算出的矿石垂直压力是随贮矿高度而变化的,从表4数据看,变化范围约7.7~13.4倍,与试验结论不符。散体拱形公式计算出的垂直压力是恒定的,即溜井底板反映出球缺内矿石重量,球缺上部矿石重量形成的垂直压力,与矿石和井壁的摩擦阻力相平衡,故溜井底部压力试验时没有变化,与试验结论相一致。
(3)在溜井放矿的矿石移动“四区论”中,第一区的矿石是等速全断面移动[4]。根据德兴铜矿1号溜井放矿实测资料[6],溜井贮矿高度为139m,第一区长度为108m,矿石平均移动速度为2.9mm/s,是平稳、缓慢下降。因此可以确定,该区内矿石压力分布是均匀而相等的。杨森压力公式计算结果是,溜井中上部矿石压力是变化最大的地方,不可能产生这样“等速、缓慢均匀全断面”移动。只有散体拱形压力计算公式计算结果是矿石压力是均匀、相等分布的,才能产生这种现象。
(4)在溜井放矿过程中,随着溜井贮矿侧压力增大,井壁磨损速度加快[7].杨森公式计算出的侧压力是随着贮矿高度增加而增大,溜井下部井壁受到的压力比上部大,即溜井底部的井壁磨损应比上部大。实际上,贮矿溜井各处磨损是均匀的,与深度无关[8].贮矿段溜井磨损均匀,上下磨损速度非常接近[9],现实的井壁磨损与杨森公式计算结果是不相符的。
总之,杨森公式反映的溜井中矿石产生的压力变化规律与试验结论和生产中反映出的井壁磨损现象是不相符的。分析其产生的原因是该公式的推导过程中,未考虑散体矿石的自动搭拱效应,它改变了矿石的压力分布规律。因此,(1)式的压力平衡方程式是不存在的。
4 结束语
从杨森压力计算公式推导的三点假设看,该公式是适合于大豆、小米等粮食作物和类似的物料,不适合矿山溜井中的矿石。同时,散体矿石存在自动搭拱效应,因此,溜井中微分薄层的压力平衡方程式(1)式是不存在的。现实中溜井中矿石压力计算是使用杨森公式,由于是其形式简单计算方便[10];计算结果偏大,属保守、可靠;未能找到更合适的计算公式等原因。散体拱形压力计算公式更适合于溜井矿石压力计算。但溜井中的矿石是一个复杂的体系,压力计算公式是一个重大的基础理论问题。因此,对上述计算公式还需从试验和生产上进一步加以证实,理论上进一步完善。

