强磁干扰环境下无人机航向的修正方法研究

张宝译

（山东师范大学信息科学与工程学院，山东 济南 250358）

现今，无人机被应用在测绘、安防、巡检等多个领域。姿态信息（俯仰角、横滚角、航向角）是决定无人机飞行稳定的重要因素之一。姿态信息中，航向角十分重要，其多采用磁力计测量所在位置的磁场信息，与当地地球磁场信息进行数据融合处理来确定，以此获得无人机的初始航向角以及修正陀螺仪的时间累计误差，维持无人机航向角的正确与稳定。但是在强磁干扰环境下，无人机上的磁力计传感器测量的数据不再是所在位置的地磁信息，不能够确定无人机的航向角，而无人机航向角度不准确会直接影响无人机的位置信息的计算，极易发生飞行事故。因而，强磁干扰环境下如何准确得到符合无人机高动态控制要求的航向角度的研究关系到无人机的正常控制和飞行安全，具有十分重要的工程应用价值，对其研究具有非常重要的意义。

在强磁干扰环境下，磁力计无法使用，可以使用其他手段获得角度。比如，使用差分定向技术测量航向角度信息，但是差分定向技术输出测量角度的频率慢（5～10Hz）、精度低（与两天线之间的距离有关），无法满足无人机的高动态控制要求，不能直接使用，因此必须将差分航向角度与无人机姿态信息进行融合处理，从而得到动态性能好、准确度高的无人机航向角数据。文章对差分定向测量的航向角与无人机姿态信息如何进行数据融合处理进行研究，给出了一种实时、便捷的数据融合方法。

1 无人机姿态更新概述

1.1 姿态更新方法

用于无人机姿态更新的算法有许多种，如方向余弦法、欧拉角法、四元数法等。

四元数是定义由4个元构成的数：Q(q0,q1,q2,q3)=q0+q1i+q2j+q3k，其中，q0、q1、q2、q3是实数，i、j、k既是互相正交的单位向量又是虚单位。

三维空间的任意一次旋转，都能够用三维空间内的某一个轴旋转一定的角度来表示。这种方法中，某一个轴可以用三维向量(x,y,z)表示，一定的角度可以用θ表示。简单地说，三维向量(x,y,z)和角度θ组成的四维向量(θ,x,y,z)可以表示出三维空间内的任意旋转。其中，三维向量(x,y,z)用来表示旋转轴的方向，因此可以用单位向量来表示此旋转轴的方向。

单位向量(x,y,z)旋转θ角度的四元数为。相较于欧拉角法和旋转矩阵法，四元数法表示更加紧凑，计算量也小一些，是一种比较常用的方法。文章姿态更新采用四元数更新算法。

1.2 强磁干扰环境下航向角测量概况

在强磁干扰环境下，磁力计无法使用，因此需要寻找一种能够不受强磁环境干扰稳定输出航向角度的传感器或设备。

差分GPS设备可以利用RTK双天线技术，将2根天线固定在载体的特定位置，根据载波相位差分原理，计算出载体在大地坐标系的航向角。因此，可以在无人机上的固定位置放置2根GPS天线，通过差分定向技术获得无人机的航向角。

差分定向获取的航向角度，更新频率慢、精度低，不能满足无人机高动态控制要求，无法直接使用。为了满足无人机飞行控制对于航向角度高动态、实时性和准确性的要求，文章提出一种以差分定向测量航向角为标定量，实时计算（修正）无人机航向角的方法。既解决了强磁干扰下无航向纠正信息导致的航向角度错误问题，也解决了强磁干扰下无航向纠正信息导致的在航向角度计算上的陀螺仪时间累计误差，使得无人机可以在强磁干扰下，依然可以获取稳定的航向角度信息。

2 强磁干扰环境下无人机航向的修正技术

2.1 无人机航向角修正技术思路及难点

无人机采集自身陀螺仪、加速度计等传感器数据，采用相关算法实时计算其姿态，得到包含姿态信息的数据，如四元数。无人机更新姿态的简要流程图如图1所示。

在强磁干扰环境下，磁力计无法使用，可根据图1计算出的四元数Qb，不能保证包含正确的航向角姿态信息。为此，设计一种方法，不再使用易受强磁干扰的磁力计，使用不受强磁干扰影响的差分定向技术获取无人机的航向角度原始值，修正无磁力计传感器数据参与而计算出的包含姿态信息的四元数Qb，经过数据融合处理，最终得到经过修正的四元数Qc。该方法的难点，也是文章研究的重点，是如何将差分定向获取的航向角度原始值与正常姿态更新计算出的姿态数据进行数据融合，进而得到经过修正的姿态数据Qc。该方法的流程图如图2所示。

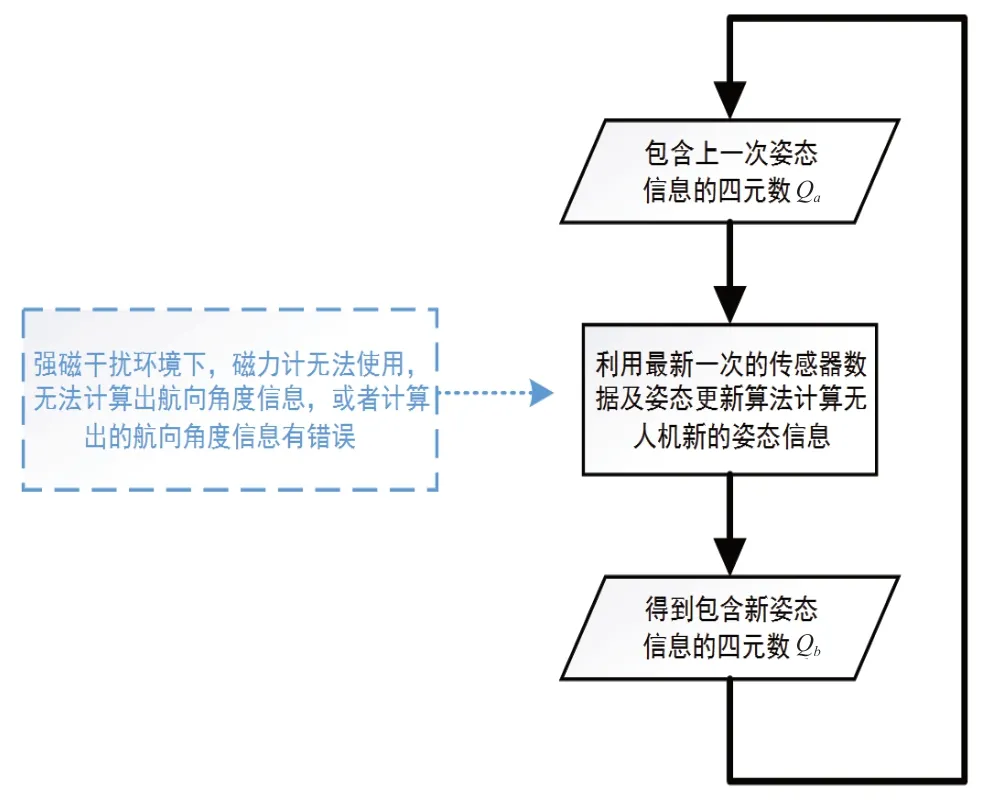
图1 姿态更新简要流程图

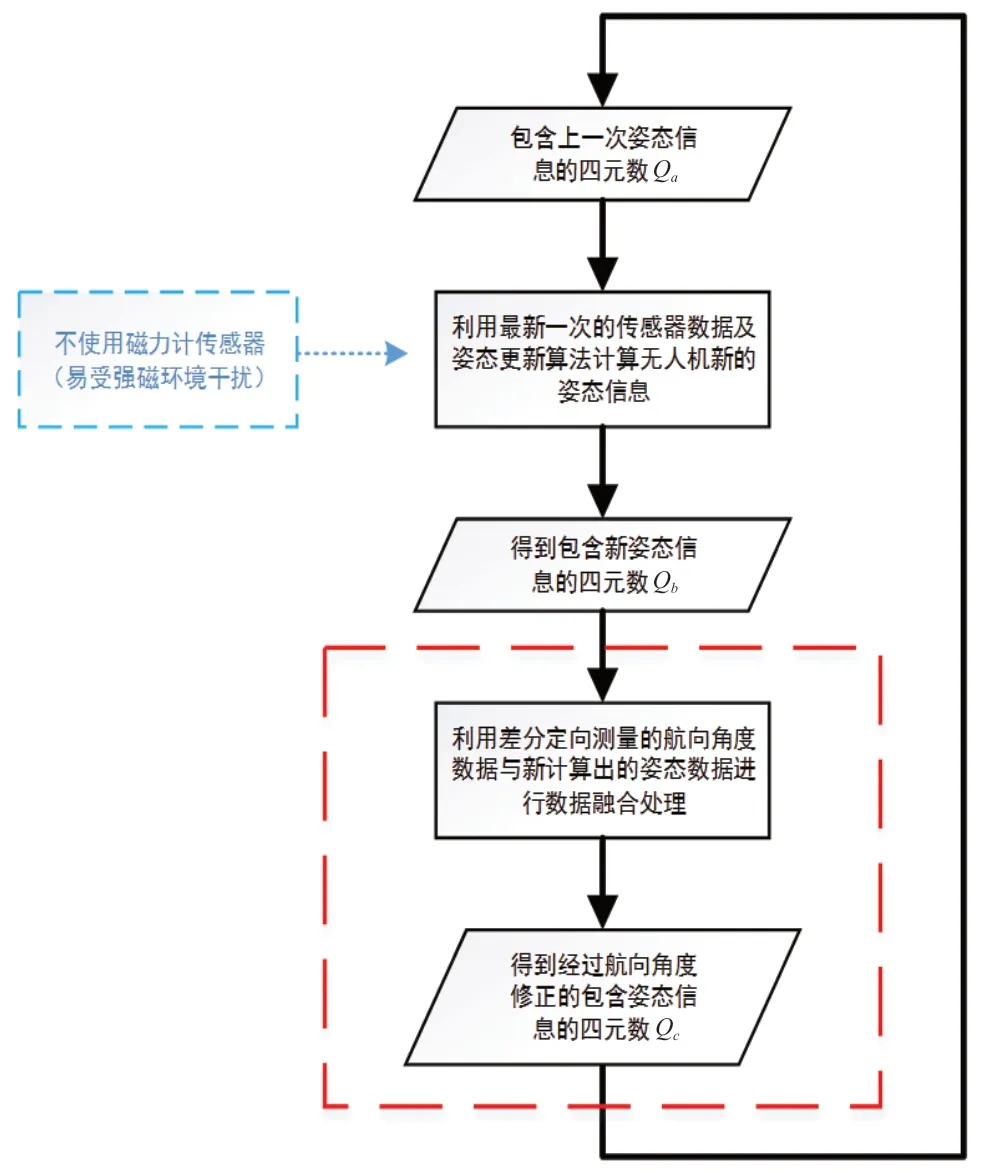
图2 文章所用方法的基本流程图

图2中，利用差分定向测量的航向角度数据与新计算出的姿态数据进行数据融合处理是本方法的难点与创新点，其原理是将差分定向测量的航向角作为标定量，新计算出的姿态数据中的航向角作为待修正量，两者之间的差值即为航向角度修正量。将待修正量修正到标定量上，可以等效为一次三维空间内的旋转。假设无人机使用的导航坐标系方向为（NED-北东地），那么此次修正的旋转轴为(0,0,1)，旋转的角度即为修正量。

2.2 无人机航向角修正技术实现方式

无人机姿态更新系统使用不含磁力计数据的传感器数据、上一次四元数数据Qa，按照正常流程进行姿态计算，迭代计算出新的四元数Qb。

假设四元数Qb里包含的航向角度为βb，差分定向技术测量的无人机航向角度为βrtk，则两者之差为航向角度初始修正量βb=(βrtk-βb)。

航向角度初始修正量乘比例因子k，得到航向角度修正量βdiffer=(k·βd)。

构建旋转四元数Qr=[cos(βdiffer/2),0,0,sin(βdiffer/2)]

根据四元数与旋转之间的关系，利用Qr与Qb的四元数乘法运算，实现修正航向角度的目的，即QC=QrQb（符号代表四元数乘法）。

假设四元数QC=(qc0,qc1,qc2,qc3)，四元数Qb=(qb0,qb1,qb2,qb3),则：

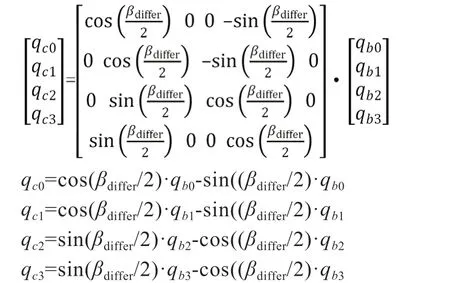
由此可得，四元数QC为经过差分航向角度修正的四元数。可以根据无人机系统控制需要直接利用四元数进行飞行控制，也可以将QC转换为姿态角用于无人机的控制。

3 方案实施过程中遇到的问题及解决方法

在现阶段调研的产品中，差分定向测量航向角的频率，最高为10Hz，一般为5Hz。而无人机姿态计算的频率一般为200Hz或更高。因此，以陀螺仪传感器为主的无人机自主姿态计算为主，当差分定向航向角度输出时，再对姿态四元数进行修正。

使用差分定向技术获得的航向角，其精度为0.5/L（L为2根天线之间的距离），单位为°。由于无人机大小的限制，2根天线的距离一般在40～80cm，其精度为0.625～1.25°。

由于差分定向测量角度的精度偏低，因此将其作为标定量，在差分定向标志位指示差分定向数据可用时，以差分定向测量角度与此时解算角度求差，然后乘比例系数，得到需要修正的角度量。

比例系数k可根据工程实际需要进行调节，差分定向测量精度不高，比例系数过大，每次得到的航向角度修正量就会偏大，造成航向角度修正过于“猛烈”，不利于电机的响应及无人机的控制。如果比例系数过小，得到的航向角度修正量就会偏小，虽然在修正航向角度的“平滑性”上会好，但是会造成修正时间过长、延时过大、实时性下降，不符合无人机控制的高动态性要求。

4 实验及数据分析

4.1 静态实验

安装好双天线（天线距离约0.5m）的无人机，静止放置在户外空旷处。采集同一时间段内（20min），经过差分定向测量航向角修正的无人机航向角度和差分定向测量的航向角度，并分析2组数据的均值和方差。

4.2 动态实验

无人机在空中做快速转动的过程中，动态实验航向角度数据对比图如图3所示。其中，采集差分定向测量的航向角度如图3中虚线所示，经过差分定向数据修正的航向角度如图3中实线所示。

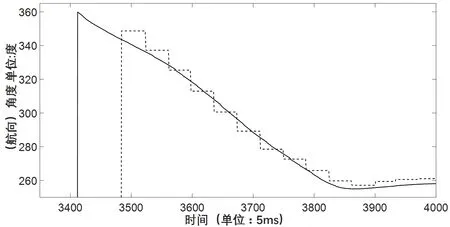
图3 动态实验航向角度数据

4.3 实验数据分析

（1）静态实验数据。差分定向测量的航向角度方差为0.0633，均值为205.2386。经过修正的航向角度，其方差为0.0273，均值为205.2704。经过修正的航向角相较于差分定向测量航向角，方差更小，曲线更为平滑，且无角度漂移现象发生，始终被差分定向测量航向角修正，维持在正确的航向角度上。

（2）动态实验数据。图3中的的数据显示，经过修正的航向角度不仅维持了实时性好的特点，而且始终被差分测量航向角度修正，且瞬时波动值更小。从图3的两条曲线可以看出，经过修正的航向角度的平滑性明显优于差分定向原始测量角度。

（3）实验结果总结。通过对无人机在静止和运动状态下采集的数据进行分析可以得出，利用文章所提方法进行修正的航向角度不仅维持了高实时性、高平滑性，而且始终被差分航向角度准确修正，没有发生时间累积误差，完全满足了研究要求，能够解决无人机在强磁干扰环境下的航向角度测量问题。

5 结束语

普通无人机通常使用磁力计传感器来确定航向角度，在强磁干扰情况下（如钢铁结构大桥附近、高压电线附近或地下铁矿附近等）不能正确测量航向角，容易导致无人机控制异常，影响飞行器自身及周边人员、环境的安全。为此，文章设计了一种方案，利用差分定向技术获取航向角度，并提出了一种利用差分航向角与无人机自身姿态更新数据进行融合处理的方法，该方法实用、快速，能够在强磁干扰环境下准确获得无人机航向角度，保证了无人机在强磁环境下的飞行安全，具有十分重要的实用价值。