基于联合抗噪算法的滚动轴承故障诊断研究

刘 冲

（华东交通大学电气与自动化工程学院，江西 南昌330013）

滚动轴承广泛存在于机械设备，由于滚动轴承的工作环境恶劣且噪声情况复杂，故障尺寸微小又难以直接观察，业界普遍采用数据驱动的方式实现故障诊断，但是振动信号易受噪声污染，使得有效特征难以被提取，因此如何提高滚动轴承在复杂噪声环境下故障诊断的准确性，成为了当前研究热点。

随着计算机、传感器的迅猛发展，机械设备的状态检测进入了“大数据”时代[1]。 使得故障诊断技术向深度学习方向发展。 深度学习模型依靠其多个隐含层，在特征提取和分类方面的卓越表现，在故障诊断领域取得了较多研究成果。 Long 等[2]将原始振动信号转换为二维图像，使用LeNet-5 模型对二维图像进行故障诊断。 2016 年Turker 等[3]提出了一种含有3 个改进的卷积层和2 个全连接层的一维卷积神经网络，直接以原始电流信号为输入，准确率达到了97.2%。 Chen[4]提出了一种单卷积层和2 个全连接层的二维卷积神经网络模型，并将算法应用于齿轮箱故障诊断。 张西宁，向宙等[5]用堆叠卷积自编码进行轴承故障诊断，使得诊断精度从79.9%提高到92.1%。 向宙等[6]用改进的区分自编码网络对不同工况下的轴承数据进行诊断，使得所提出的区分型网络的特征提取能力不受工况影响。 虽然很多基于卷积神经网络的研究已经取得较好诊断效果，但仅证明了模型在使用无噪声实验数据的有效性。然而，振动信号易受噪声污染。近年来，为了提高模型的抗噪能力，一些训练技巧(如使用dropout 操作[7]）和结构改进(如添加AdaBn 层[8]）的方法被提出来，在图像降噪领域，Zhang 等[9]提出一种基于深度卷积神经网络的非固定噪声模板图像训练方法。 Mao[10]等提出了一种基于深度卷积去噪自编码的图像降噪方法。 然而这些方法仅适用于二维或者三维图像的降噪。 目前针对一维振动信号降噪的方法大多基于信号处理技术，如黄正平等[11]提出一种基于MED 和Teager 能量算子的故障诊断模型，能有效消除信号的带内噪声，但是信号处理技术过于依靠人工特征提取，费时费力。 因此，本文提出一种基于全卷积网络（fully convolutional networks，FCN）[12]的一维卷积降噪自编码器（1D-convolutional denoising auto-encoder ，1D-DCAE）与一维卷积神经网络（1-D convolutional naural network，1D-CNN）联合的诊断方法来解决上述问题。 前者对原始信号降噪，后者对1D-DCAE 输出的降噪信号进行故障诊断。此外，1D-DCAE 模型了舍弃池化层以减少1D-DCAE 在数据重构过程中造成的信息丢失，从而提升降噪能力。

1 卷积降噪自编码和卷积神经网络结构

1.1 一维卷积神经网络

卷积神经网络（convolitional neural network，CNN）是一种多模块的前馈神经网络，传统CNN 的结构主要由特征提取模块和分类模块2 个部分组成，特征提取模块由输入层、卷积层、激活函数、池化层组成，分类模块包含全连接层和分类层。 特征提取模块的作用是从数据中提取特征，分类模块实现对隐层特征的回归和分类。 卷积层是CNN 提取特征的关键，卷积层由一组滤波器组成，滤波器由多个神经元组成，神经元都只与输入层中的神经元局部连接， 且每个滤波器中的神经元共享权值， 这也是CNN 能减少网络参数的根本原因。 第k 个滤波器的滤波操作的公式为

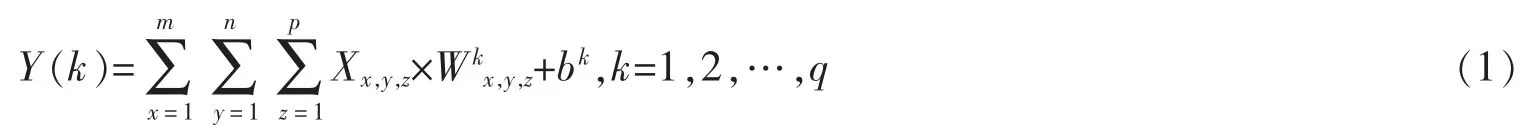
式中：Y（k）为第k 个滤波器学到的特征图；X 为输入；x，y，z 为输入数据的维度；Wkx，y，z，bk为第k 层的权重和偏置。

卷积层的输出经ReLu 函数激活后输入池化层，池化层是下采样的过程，其作用是对卷积层学习到的特征降维，提取重要纹理特征。全连接作用是将特征提取模块学习到的分布式特征表示映射到样本标记，起到分类器的作用，但由于其庞大的参数量可能会导致网络陷入拟合，大量的参数也会大量增加训练时间，影响算法的时效性。 针对以上的问题，1D-CNN 采用全局平均池化(global average pooling)作为分类器，全局平均池化能对特征提取模块学习到的高维特征直接降维，因其本身没有可供学习的特征，于传统的全连接层相比，全局平均池化极大地减少了网络的参数。

联合诊断模型基于1D-CNN 来诊断滚动轴承故障，1D-CNN 的模型和参数如图1 所示，模型由3 个卷积层、2 个最大池化层、1 个全局平均池化层组成，在特征学习方面采用卷积层和池化层交替来实现，分类器选用的是全局平均池化层而不是传统的全连接层。 其中，20@32 表示该层使用32 个长度为20 的卷积核进行卷积运算，模型的卷积核和池化核均为一维结构，以适应一维振动信号。

图1 1D-CNN 结构Fig.1 Structure of 1D-DCAE

1.2 一维卷积降噪自编码

传统的自编码器（auto encoder，AE）由编码器和解码器两部分组成，编码器经非线性映射对输入X 降维，得到隐藏层表示Z，解码器由另一个非线性变换将隐藏表示Z 映射回重构数据

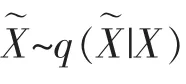
传统的DAE 是基于全连接网络的，但是全连网络参数过多，网络容易陷入过拟合。 针对该问题，本文提出一种基于FCN 的1D-DCAE 模型。FCN 是一种特殊类型的卷积神经网络，FCN 和CNN 两者之间的区别是FCN 移除了全连接层，与基于全连接层的DAE 相比，FCN 主要优势有两点：①移除全连接层能减少参数数量和网络过拟合风险；②FCN 使得每个输出特征图相互关联，能保留原始输入的局部空间信息。 此外，为了让输入和输出信号精准匹配，基于FCN 的1D-DCAE 模型没有使用池化层，因为池化层可能会造成信息的少量细节丢失[14]。

本文使用1D-DCAE 对含噪信号做降噪处理，以联合诊断模型的抗噪能力，与CNN 类似，1D-DCAE 也能通过增加深度来提升重构能力。

图2 1D-DCAE 结构Fig.2 Structure of 1D-DCAE

式中：Pz为原信号功率；Pn为噪声信号功率。

1.3 1D-DCAE 和1D-CNN 的联合诊断流程

基于联合算法的诊断流程主要分为5 个阶段：①以1 dB 为间隔，在原始数据集中分别加入SNR=-2～9 dB 范围的高斯白噪声，共得到11 种不同的噪声信号；②将得到的每种噪声分别按4∶1 分为训练集和测试集，将SNR= -2，0，2，4，6，8 dB 环境下的6 种噪声训练集混合并洗牌，用于训练1D-DCAE，所有的测试集用于测试模型性能；③用混合高斯噪声的训练样本x˜对1D-DCAE 训练，完成1D-DCAE 的训练后，得到降噪的训练样本xˆ；④将降噪后的训练样本xˆ作为1D-CNN 的输入，利用训练样本标签完成模型训练；⑤将测试样本输入联合诊断模型，完成轴承故障的诊断。

2 实验验证

2.1 数据描述

实验所用滚动轴承时域振动信号来自美国西储大学轴承中心，信号采样频率为12 kHz。 故障类型为内圈故障、外圈故障、滚球体故障，故障的损伤直径分别为0.18，0.36，0.54 mm 三种程度故障，有9 类故障加正常状态共计10 类数据样本。 本次所有实验数据均在0 负载情况下采集，每0.1 s 采集一次数据，每个样本长度为1 200 个数据点，每类样本采集1 000 个，共计10 000 个样本，其中4/5 的样本用于训练，其余的样本用于测试。 实验使用深度学习框架Tensorflow，处理器为i7-4790@3.60 GHz，内存为8 GB 硬件平台进行实验。

2.2 基于1D-DCAE 的降噪实验

本文实验结果由两部分组成：一部分为1D-DCAE 的重构误差，另一部分为1D-CNN 的诊断精度，以此来验证联合抗噪算法的有效性。 前者重构误差所反映的是1D-DCAE 降噪效果，后者诊断精度验证了本文算法在噪声环境下的诊断效果。

1D-DCAE 训练参数和超参数设置如下：学习率设为0.01，epochs 设为50，batchsize 设为100，DAE 的输入、隐藏层、输出维度分别设为1 200，600，1 200，激活函数为ELU。 为了验证池化层对1D-DCAE 算法去噪效果的影响，将本文提出改进的1D-DCAE 与经典1D-DCAE 的进行比对，除了含有池化层之外，其余参数与改进的1D-DCAE 算法一致，每组实验重复10 次，实验结果如表2 所示。

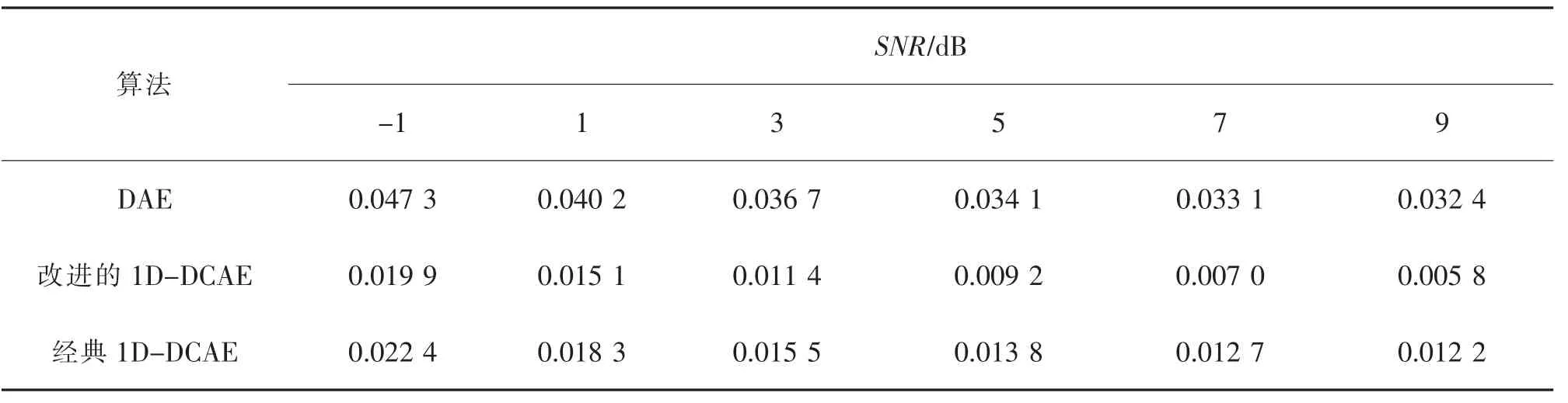
表1 在不同信噪比下DAE 和1D-DCAE 的重构误差Tab.1 Reconstruction errors of DAE and 1D-DCAE under different SNR

由以上实验结果可知， 在所有信噪比环境下， 改进的1D-DCAE 的重构误差均小于DAE 和标准的1D-DCAE 算法。 实验结果表明， 改进的1D-DCAE 算法降噪效果最好， 卷积自编码模型去噪能力强于DAE，原因如下：①由于1D-DCAE 的结构较深，其特征重构能力优于DAE；②1D-DCAE 的参数远少于DAE。 其中，1D-DCAE 的参数数量为2×（20×16+5×32×16+5×64×32）=26 240，DAE 的参数数量为1 200×600×2=1 440 000，所以1D-DCAE 算法在噪声环境下不易过拟合。 当SNR>5 dB 时，改进的1D-DCAE 算法的重构误差随着信噪比的增加不断减小，而标准1D-DCAE 的重构误差几乎没有变化，其原因是在高信噪比环境下，标准1D-DCAE 造成信息丢失大于降噪得到的收益。 因此，舍弃池化层能提升对振动信号的降噪效果，并且减少模型对输入数据的信息丢失。

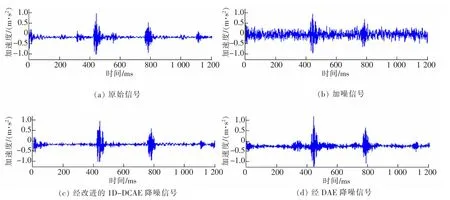
图3 信号图Fig.3 Figures of signals

2.3 联合算法的故障诊断

本文使用1D-CNN 对降噪信号进行故障诊断，1D-CNN 的训练参数和超参数设置如下：epochs 为120，学习率为0.001，batchsize 为100， 重复10 次实验，1D-CNN 在不同信噪比条件下的诊断结果如图4 和表2所示，在SNR=-1 dB 时的诊断高达96.2%，SNR>1 dB 时，诊断精度能达到98.5%以上。 因此，联合诊断方法能自适应的处理任何噪声环境，即使是较低信噪比的噪声环境下。

为了验证本文联合诊断方法的有效性，本文算法与DCE+1D-CNN，未降噪处理+1D-CNN 进行实验结果的比对，在SNR= -1 dB 噪声环境下，DCE+1D-CNN 联合诊断的方法和1D-CNN 的诊断正确率分别下降至93.86%和84.55%。 实验结果表明， 在低信噪比环境下， 本文所用的1DDCAE 对数据进行降噪处理，能有效的提升诊断精度。

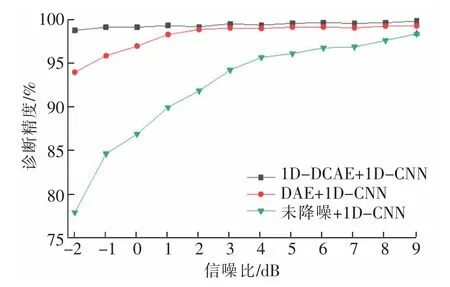
图4 1D-CNN 在不同降噪方法下的诊断精度Fig.4 Diagnosis accuracy of 1D-CNN with different denoising processes

表2 1D-CNN 在不同降噪方法下的诊断精度Tab.2 Diagnosis accuracy of 1D-CNN with different denoising processes %

图5 t-SNE 特征学习可视化Fig.5 Feature learning visualization with t-SNE

2.4 特征可视化

本文为了证明1D-CNN 在噪声环境下的特征提取能力，在SNR=1 dB 的噪声环境下，采用了t 分布随机近邻嵌入流形学习算法（T-SNE）将特征降维至2 维，对输入层和三个卷积层进行特征可视化， 其中每一种颜色表示一种故障类别，每一个点表示一个样本， 可视化结果如图5 所示，a，b，c，d 从左至右分别为输入，Conv4，Conv5，Conv6 的特征可视化结果。

3 结论

提出一种基于1D-DCAE 和1D-CNN 联合抗噪诊断算法。 该方法能有效解决复杂噪声环境下的故障诊断问题，提高了系统的抗噪能力。 对实验结果进行分析得出以下结论：

1） 基于FCN 的1D-DCAE 对于轴承信号的降噪效果均优于传统DAE 和经典DCAE 算法， 即使在SNR= -1 dB 低信噪比环境下，1D-DCAE 算法的重构误差仅为0.019， 在SNR>5 dB 的高信噪比环境下，重构误差小于0.01，表明本文提出算法在舍弃池化层后，在数据重构过程几乎没有造成信息丢失。

2） 经1D-DACE 降噪后，1D-CNN 即使在SNR= -1 dB 低信噪比噪声环境下， 其诊断精度达到了96.2%，SNR>1 dB 时，诊断精度能达到98.5%以上，若未作降噪处理，其诊断精度仅为84.6%。 结果表明联合诊断算法能实现对各种噪声环境下的故障精准诊断。