基于土壤微波辐射布儒斯特角反演土壤含水率

马红章，艾 璐，刘素美，孙根云，孙 林

基于土壤微波辐射布儒斯特角反演土壤含水率

马红章1，艾 璐1，刘素美1，孙根云2，孙 林3

（1. 中国石油大学（华东）理学院，青岛 266580；2. 中国石油大学（华东）海洋与空间信息学院，青岛 266580；3. 山东科技大学测绘科学学院，青岛 266590）

在利用被动微波遥感技术进行裸露地表土壤含水率（Soil Moisture Content，SMC）的反演中，土壤粗糙度是制约反演精度的最关键因素。该研究利用改进的积分方程模型（Advanced Integral Equation Model，AIEM）进行地表多角度微波发射率的模拟，探索地表微波辐射多角度信息用于提高地表SMC反演精度的可行性。基于不同SMC和不同粗糙度地表多角度V极化发射率数据的变化趋势提取土壤介质布儒斯特角，结果表明，土壤布儒斯特角对SMC具有较高的敏感性，C波段（6.6 GHz）不同含水率土壤的布儒斯特角分布在60°～80°范围内。基于AIEM模拟数据的分析发现，土壤布儒斯特角正切值与SMC具有较好的线性关系，线性拟合决定系数为0.94，均方根误差为0.027 cm3/cm3，并得到了基于布儒斯特角的裸露地表SMC反演算法。基于模拟数据的算法验证结果表明，算法的SMC预测值与理论值的决定系数为0.95，均方根误差为0.024 cm3/cm3。算法在不同土壤粗糙度自相关函数下均表现出稳健的特性，SMC预测精度最大均方根误差为0.027 cm3/cm3，最小为0.023 cm3/cm3。基于布儒斯特角的SMC反演算法利用的是多角度土壤发射率的相对变化而非其绝对数值，该研究为SMC的多角度被动微波遥感提供了一种不同的研究思路。

土壤；水分；遥感；粗糙度；被动微波辐射；布儒斯特角

0 引 言

土壤含水率（Soil Moisture Content，SMC）在陆气能量交换过程中扮演着非常重要的角色，也是气候模型、水文模型和干旱检测模型等的主要输入参数，因此，SMC时空变化信息的准确获取可为农业生产和旱涝灾害监测提供重要的依据[1-3]，同时对水资源管理以及气候变化等相关研究也都具有重要的学术意义和应用价值[4-6]。目前，基于光学和微波遥感技术进行大范围土壤水分的监测研究已经得到了长足发展[7-8]，其中，微波对云有较强的穿透能力，具有全天时、全天候的观测能力且微波对SMC具有较高的敏感性，在土壤水分监测中具有独特优势，微波遥感已成为地表SMC反演的主要技术手段之一[9-11]。

土壤粗糙度是制约微波遥感土壤水分精度的最主要因素，如何降低地表粗糙度对SMC反演的影响一直是该领域的研究重点。在地表SMC的被动微波遥感中，土壤微波发射率可表示为SMC和土壤粗糙度的非线性复合函数。Jackson在忽略土壤粗糙度影响的前提下，基于大量的实测地表辐射亮温与SMC数据，通过统计回归方法建立了地表微波发射率与SMC线性关系的单通道算法[12]，单通道算法虽简单但土壤粗糙度的影响制约了算法的反演精度。近年来，基于电磁波传输理论的地表微波辐射理论模型取得了显著的发展，小扰动模型、物理光学模型和几何光学模型等是发展较早的传统理论模型的代表，后期又发展了积分方程模型（Integrated Equation Model，IEM）和改进的IEM模型（Advanced Integral Equation Model，AIEM）。土壤微波散射IEM模型是使用较广泛的一个面散射模型，有较广的粗糙度适用范围[13]，但由于IEM模型对实际地表粗糙度的刻画并不十分准确以及不同粗糙度条件下土壤菲涅尔反射系数的计算采取了分段的处理方式，导致IEM模型对不同粗糙程度地表微波辐射的模拟精度存在差异。针对IEM模型的不足，Wu等[14]通过可计算任意粗糙度条件下土壤Fresnel反射系数的连续模型对IEM模型进行了改进，但模型在不同频率条件下对土壤Fresnel反射系数的估算仍有差异。Chen等[15]通过构建过渡函数使Fresnel反射系数在高低频均可采用相同的计算方法并通过订正粗糙度功率谱函数，使模型模拟精度得到进一步提高，改进后模型被称为AIEM模型。通过与蒙特卡洛模拟数据和试验观测数据的比较证实了AIEM模型较IEM模型不仅有更宽的粗糙度适用范围而且具有更强的模拟宽波段和大角度辐射数据的能力[16-18]。

为消除地表粗糙度影响，提高SMC反演精度，国内外学者基于观测数据或理论模型模拟数据，发展了土壤粗糙度参数化的经验或半经验模型，如Dubois模型[19]、Oh模型[20]、Q/H模型[21-22]和Shi模型[23]等，而这些参数化模型的发展受限于特定的地表类型、固定的观测角度数据以及采用的近似条件等，导致粗糙度参数化方案在大面积应用中仍然存在不确定性，由此发展的SMC算法在不同地表条件下的反演精度也有待进一步提高。欧空局的土壤水分和海洋盐度卫星（Soil Moisture and Ocean Salinity，SMOS）具备地表多角度微波辐射的观测能力，多角度观测数据在土壤水分反演中也具备更大的应用潜力[24]，但目前基于多角度地表微波辐射观测数据进行SMC反演中却没有考虑角度对粗糙度影响的差异性，导致多角度数据的应用潜力未得到充分利用。本研究基于AIEM模型，分析地表微波发射率多角度模拟结果，探索地表微波辐射多角度特征在地表SMC反演中的应用，以期为土壤水分反演提供一种可靠方法。

1 材料与方法

1.1 土壤样本

本研究以中国黄河流域分布广泛的砂质土壤为研究对象，土壤的砂土质量分数高于40%，黏土质量分数低于20%，土壤容重为1.0～1.4 g/cm3范围内。土壤温度设定在适于植被生长的10～35 ℃，以粗糙度均方根高度（，cm）和相关长度（，cm）2个参数表征土壤粗糙度的变化，以单位体积土壤中水分的体积（体积含水率，cm3/cm3）来表示土壤含水率。

1.2 基于AIEM模型计算土壤微波发射率

AIEM模型主要输入参数包括微波频率、土壤介电常数、观测角度以及表征土壤粗糙度的均方根高度和相关长度，模型可模拟土壤微波双站散射系数，进而可通过式（1）计算土壤的多角度微波发射率。

模型输入参数中的土壤介电常数选用Dobson模型[25]计算，Dobson模型主要计算公式为

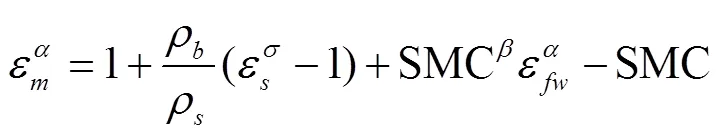
1.3 基于布儒斯特角的土壤含水率反演模型构建方法

1.3.1 土壤布儒斯特角的计算方法

电磁波在2种各向同性电介质的分界面上发生反射和折射时，反射电磁波的偏振状态会发生改变且偏振程度与入射角有关。当入射角度等于某一特定角度时，反射电磁波偏振化程度最高且反射波与透射波垂直[26]，此角度称为该介质的布儒斯特角。当电磁波入射到空气土壤分界面上且电磁波入射角度等于布儒斯特角时，电磁波的垂直极化分量会被土壤介质最大程度的吸收，根据能量守恒原理，当观测角等于布儒斯特角时，土壤介质垂直极化发射率会达到最大。不同含水率土壤的布儒斯特角计算过程如下：1）基于AIEM模型对不同含水率土壤的V极化发射率进行1°间隔的模拟，以发射率最大值所对应的角度作为布儒斯特角的近似值，确定不同条件下土壤布儒斯特角的最大变化范围；2）以5°为间隔取多个角度（覆盖布儒斯特角最大变化范围）的发射率数据，利用三次多项式回归得到发射率随角度的变化方程，由方程的一阶导数等于0所对应的角度确定布儒斯特角。

1.3.2 土壤布儒斯特角与SMC的关系

设电磁波以1入射角从折射率为1空气介质入射到折射率为2的土壤介质层时，折射角为2，根据菲涅尔定律，有

当入射角1等于布儒斯特角时，满足反射电磁波与折射电磁波相互垂直，即12=90°，因此，土壤介质的布儒斯特角（θ，（°））等于土壤与空气两者折射率之比的反正切值。

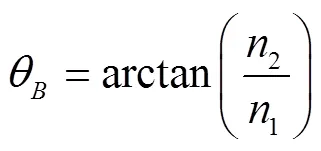
对于微波波段电磁波，空气的折射率1=1，土壤介质的折射率2可表示成土壤介电常数的函数，而土壤介电常数主要由SMC决定，因此，SMC可用土壤介质布儒斯特角正切值的函数来计算：

2 结果与分析

2.1 不同含水率土样的布儒斯特角计算结果

固定AIEM模型和Dobson模型的输入参数（土壤容重为1.2 g/cm3，土壤温度为15 ℃，土壤的砂土质量分数为50%，黏土质量分数为10%，土壤粗糙度均方根高度为1.25 cm，相关长度为10 cm）。在SMC 4个等级上（0.05、0.15、0.25、0.35 cm3/cm3）以1°为间隔模拟土壤V极化发射率随观测角度的变化，如图1所示，不同含水率土壤的布儒斯特角分布在60°～80°的变化范围内。在该范围为以5°为间隔取5个角度（60°、65°、70°、75°、80°）的发射率数据，利用发射率随角度变化的三次多项式回归方程，求一阶导数确定布儒斯特角，可知，对应土壤SMC 4个等级的布儒斯特角分别为64.8°、72.1°、75.7°和77.7°。

注：土壤容重为1.2 g·cm-3；土壤温度为15 ℃；土壤砂土质量分数50%，黏土质量分数10%；土壤粗糙度均方根高度和相关长度分别为1.25和10 cm。

2.2 布儒斯特角对SMC的鲁棒性分析

AIEM模型和Dobson模型的输入参数中除SMC外，其他输入参数如土壤粗糙度、土壤容重以及土壤温度等均有可能引起土壤布儒斯特角的变化，而影响布儒斯特角与SMC的相关性，因此进行不同条件下的布儒斯特角对SMC鲁棒性分析是很有必要的。以C波段（6.6 GHz）为例，AIEM模型中粗糙度自相关函数采用高斯相关，为避免布儒斯特角计算的误差，依然采用1°为间隔的角度密集型模拟策略，直接由发射率大小变化来确定布儒斯特角。

2.2.1 土壤温度对布儒斯特角的影响

设定土壤容重为1.2 g/cm3，土壤的砂土质量分数50%，黏土质量分数10%，土壤粗糙度均方根高度=1.25 cm，相关长度=10 cm，在SMC 4个等级上（0.05、0.15、0.25、0.35 cm3/cm3）分别计算土壤温度由10 ℃变化到35 ℃的土壤布儒斯特角数据，如图2a所示，在4个SMC等级上，随温度的升高布儒斯特角没有出现变化，这说明布儒斯特角与SMC的关系不受土壤温度参数变化的影响。

2.2.2 土壤容重对布儒斯特角的影响

设定土壤温度为15 ℃，其他参数保持2.1节的设置，在SMC 4个等级上（0.05、0.15、0.25、0.35 cm3/cm3）分别计算土壤容重由0.9 g/cm3变化到1.4 g/cm3的土壤布儒斯特角数据，如图2b所示，土壤容重的变化对布儒斯特角的取值有轻微的影响，影响程度会随土壤湿度的增加而下降，在SMC为0.05 cm3/cm3时，土壤容重从0.9 g/cm3变化到1.4 g/cm3，布儒斯特角取值的增加量未超过2°。在SMC为0.15 cm3/cm3时，土壤容重从0.9 g/cm3变化到1.4 g/cm3，布儒斯特角取值的增加量未超过1°，当SMC超过0.15 cm3/cm3后，布儒斯特角取值不再随土壤容重的变化而变化。

2.2.3 土壤粗糙度对布儒斯特角的影响

按上述设定保持不变，在SMC 4个等级上（0.05、0.15、0.25、0.35 cm3/cm3）分别计算土壤粗糙度均方根高度（）从0.5 cm增大到3.5 cm的土壤布儒斯特角数据，如图2c所示，当土壤粗糙度均方根高度参数从0.5 cm增大到3.5 cm，在4个SMC等级下，布儒斯特角取值会出现随粗糙度的增加而有所增大的变化，但布儒斯特角的变化量均未超过2°。

2.2.4 SMC对布儒斯特角的影响

前面的模拟结果显示，土壤容重与粗糙度2个参数对土壤布儒斯特角均有轻微的影响。保持其他参数设置不变，分别计算土壤粗糙度均方根高度和土壤容重4种组合下的SMC从0.05 cm3/cm3增大到0.40 cm3/cm3的土壤布儒斯特角数据，如图2d所示，在SMC的取值范围内，土壤容重与粗糙度的4种不同组合对布儒斯特角的变化量仍然未超过2°，这说明土壤容重与粗糙度对布儒斯特角的影响并不会产生明显的累加效应。相比较而言，SMC从0.05 cm3/cm3变化到0.40 cm3/cm3，布儒斯特角变化量能达到15°，说明布儒斯特角对SMC敏感性的受土壤容重和土壤粗糙度的影响较小。

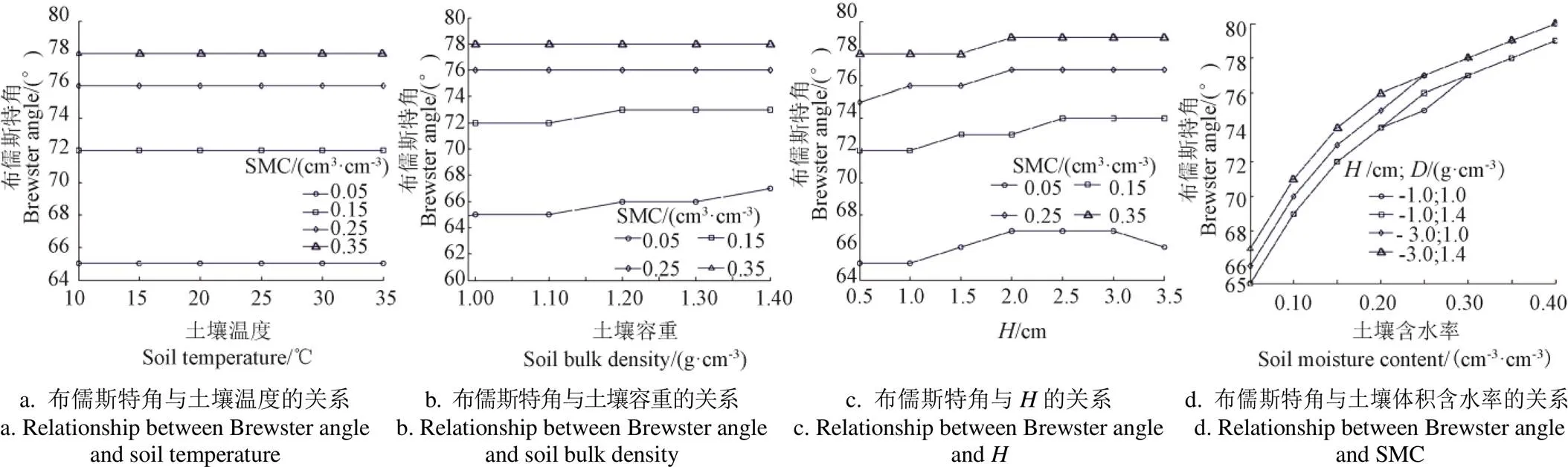
注：H和D分别为土壤粗糙度均方根高度和土壤容重。

2.3 基于布儒斯特角的SMC反演模型分析

2.3.1 模型构建及验证

利用AIEM模型进行了C波段（6.6 GHz）500种不同地表条件下的微波辐射模拟，模拟角度60°～80°，间隔5°；不失一般性，SMC、粗糙度以及土壤质地等参数均在比较大的范围内随机取值，粗糙度的刻画亦随机采用AIEM模型中自带的7种自相关函数（高斯相关、指数相关、转换指数相关、幂律谱相关数相关、-幂相关、-指数相关、类指数相关），保证模拟数据能适用于多数农田土壤粗糙度特征，模型具体输入参数如表1。

表1 改进积分方程模型（AIEM）输入土壤参数

对500组数据进行5个角度V极化发射率数据的回归拟合再进行求导运算得到其对应的布儒斯特角，选取前400组数据用于布儒斯特角正切值与SMC关系的回归，得到SMC的反演回归模型如式（6）。拟合结果如图3a所示，布儒斯特角的正切值与SMC之间有较好的线性关系，2为0.94，均方根误差为0.027 cm3/cm3。利用余下的100组数据对反演模型进行了验证，结果如图 3b所示，模型的SMC预测值与真实值间的2达到0.95，均方根误差为0.024 cm3/cm3，验证结果表明式（6）可有效计算裸露地表土壤含水率。

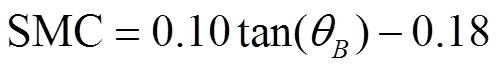
注：*表示<10-7。下同。

Note: * means<10-7. The same below.

图3 基于布儒斯特角的SMC反演模型构建与验证

Fig. 3 Establishment and verification of SMC inversion model based on Brewster angle

2.3.2 自相关函数对模型精度的影响

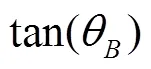
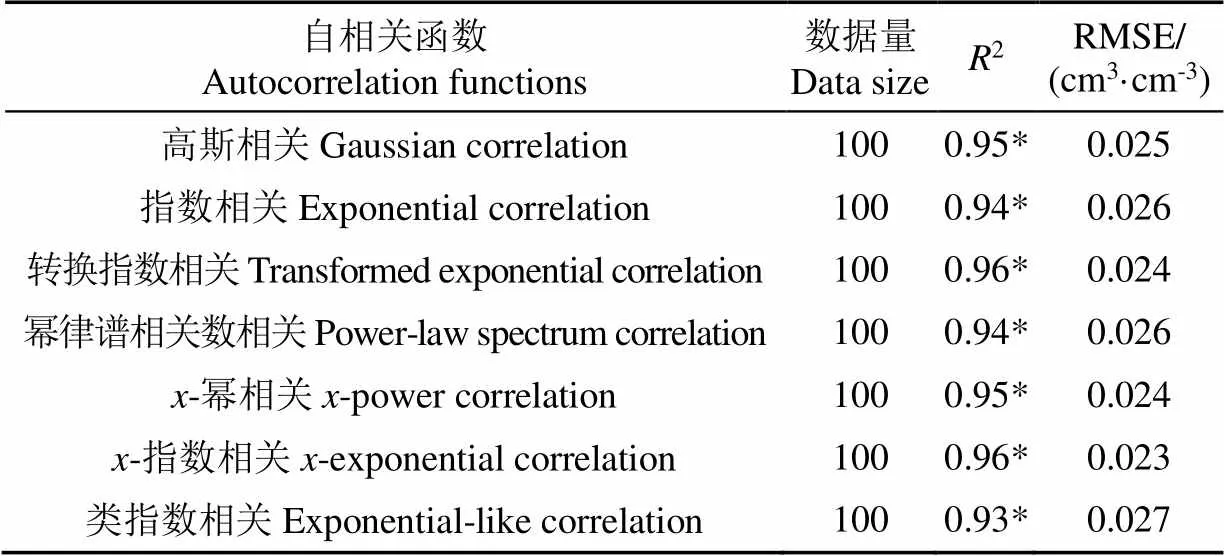
表2 不同粗糙度自相关函数下的验证结果

3 结 论

土壤粗糙度一直是影响被动微波遥感裸土土壤含水率的最大因素。本研究以地表微波辐射理论模型——改进的积分方程模型（Advanced Integral Equation Model，AIEM）为基础，通过对地表微波发射率多角度模拟数据的分析，探索多角度被动微波遥感数据在土壤水分反演中的应用潜力。结果表明：

1）在C波段（6.6 GHz），土壤布儒斯特角对土壤含水率（Soil Moisture Content, SMC）具有较高的敏感性。SMC可使土壤布儒斯特角发生15°的变化，而土壤粗糙度和土壤容重等参数对土壤布儒斯特角的影响不超过2°。

2）通过对AIEM模拟数据的分析发现，土壤布儒斯特角正切值与土壤含水率具有较好的一致性关系，线性拟合决定系数为0.94，均方根误差为0.027 cm3/cm3，基于此提出了基于土壤微波辐射布儒斯特角的土壤含水率反演算法。

3）反演算法利用了多角度土壤微波发射率的相对变化趋势，对不同的土壤粗糙度自相关函数类型算法均表现出稳健的特性。对不同粗糙度自相关函数类型，反演算法对SMC的预测精度的最大均方根误差为0.027 cm3/cm3，最小为0.023 cm3/cm3。

该研究为SMC的多角度被动微波遥感提供了一种不同的研究思路。由于目前算法还缺乏基于试验观测数据的验证，还不能证明基于AIEM模拟数据得到的反演模型在实际反演中能取得满意的结果，下一步将开展相关试验收集相关数据，验证该算法在实际应用中的可行性。

[1] Wang Hongquan, Magagi R, Goita K. Potential of a two-component polarimetric decomposition at C-band for soil moisture retrieval over agricultural fields[J]. Remote Sensing of Environment, 2018, 217: 38-51.

[2] 赵天杰. 被动微波反演土壤水分的L波段新发展及未来展望[J]. 地理科学进展，2018，37(2)：198-213. Zhao Tianjie . Recent advances of L-band application in the passive microwave remote sensing of soil moisture and its prospects[J]. Progress in Geography, 2018, 37(2): 198-213. (in Chinese with English abstract)

[3] 郭交，刘健，宁纪锋，等. 基于Sentinel多源数据的农田地表土壤水分反演模型构建与验证[J]. 农业工程学报，2019，35(14)：71-78. Guo Jiao, Liu Jian, Ning Jifeng, et al. Construction and validation of soil moisture retrieval model in farmland based on Sentinel multi-source data[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2019, 35(14): 71-78. (in Chinese with English abstract)

[4] 尹楠，姜琦刚，孟治国，等. 基于RADARSAT-2 全极化数据反演周期性地表土壤湿度[J]. 农业工程学报，2013，29(17)：72-79. Yin Nan, Jiang Qigang, Meng Zhiguo, et al. Use of fully polarimetric RADARSAT-2 data to retrieve soil moisture of periodic surfaces[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2013, 29(17): 72-79. (in Chinese with English abstract)

[5] Xu Xiaoyong, Tolson B A, Li J, et al. Comparison of X-band and L-Band soil moisture retrievals for land data assimilation[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2017, 10(9): 3850-3860.

[6] Pangaluru K, Velicogna I, Mohajerani Y, et al. Soil moisture variability in India: Relationship of land surface atmosphere fields using maximum covariance analysis[J]. Remote Sensing, 2019, 11(3): 335-339.

[7] Jin R, Li X, Liu S M, et al. Understanding the heterogeneity of soil moisture and evapotranspiration using multiscale observations from satellites, airborne sensors, and a groundbased observation matrix[J]. IEEE Geoscience & Remote Sensing Letters, 2017, 14(11): 2132-2136.

[8] Cui Y K, Xiong W T, Hu L, et al. Applying a machine learning method to obtain long time and spatio-temporal continuous soil moisture over the Tibetan Plateau[C]. Yokohama, Japan: IEEE International Geoscience and Remote Sensing Symposium, 2019: 6986-6989.

[9] 赵少华，秦其明，沈心一，等. 微波遥感技术监测土壤湿度的研究[J]. 微波学报， 2010， 26(2)：90-96. Zhao Shaohua, Qin Qiming, Shen Xinyi, et al. Review of microwave remote sensing on soil moisture monitoring[J]. Journal of Microwaves, 2010, 26(2): 90-96. (in Chinese with English abstract)

[10] Mccoll K A, Alemohammad S H, Akbar R, et al. The global distribution and dynamics of surface soil moisture[J]. Nature Geoence, 2017, 10(2): 100–104.

[11] 杨贵军，岳继博，李长春，等. 基于改进水云模型和Radarsat-2数据的农田土壤含水量估算[J]. 农业工程学报，2016，32(22)：146-153. Yang Guijun, Yue Jibo, Li Changchun, et al. Estimation of soil moisture in farmland using improved water cloud model and Radarsat-2 data[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2016, 32(22): 146-153. (in Chinese with English abstract)

[12] Jackson T J. Measuring surface soil moisture using passive microwave remote sensing[J]. Hydrol Processes, 1993, 7(11): 139-152.

[13] Zeng J, Chen K S, Bi H, et al. A comprehensive analysis of rough soil surface scattering and emission predicted by AIEM with comparison to numerical simulations and experimental measurements[J]. IEEE Transactions on Geoscience and Remote Sensing, 2017, 55(3): 1696-1708.

[14] Wu T D, Chen K S, Shi J, et al. A transition model for there flection coefficient in surface scattering[J]. IEEE Transactions on Geoscience and Remote Sensing, 2001, 39(9): 2040-2050.

[15] Chen K S, Wu T D, Tsang L, et al. Emission of rough surfaces calculated by the integral equation method with comparison to three-dimensional moment method simulations[J]. IEEE Transactions on Geoscience and Remote Sensing, 2003, 41(1): 90-101.

[16] Wu T D, Chen K S. A reappraisal of the validity of the IEM model for backscattering from rough surface[J]. IEEE Transactions on Geoscience and Remote Sensing, 2004, 42(4): 743-753.

[17] Yang Y, Chen K S, Tsang L, et al. Depolarized backscattering of rough surface by AIEM model[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2017, 10(11): 4740-4752.

[18] Shi J C, Chen K S, Li Q, et al. A parameterized surface reflectivity model and estimation of bare-surface soil moisture with L-band radiometer[J]. IEEE Transactions on Geoscience and Remote Sensing, 2002, 40(12): 2674-2686.

[19] Dubois P C, Van Z J, Engman E T. Measuring soil moisture withimaging Radars[J]. IEEE Transactions on Geoseience and Remote Sensing, 1995, 33(4): 915-926.

[20] Oh Y, Sarabandi K, Ulaby F T. An empirical model and an inversion technique for radar scattering from bare soil surfaces[J]. IEEE Transactions on Geoseience and Remote Sensing, 1992, 30(2): 370-381.

[21] Wigneron J P, Laguerre L, Kerr Y H. A simple parameterization of the L-band microwave emission from rough agricultural soils[J]. IEEE Transactions on Geoscience and Remote Sensing, 2001, 39(8): 1697-1707.

[22] Wigneron J P, Chanzy A, Kerr Y H, et al. Evaluating an improved parameterization of the soil emission in L-MEB[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(4): 1177-1189.

[23] Shi J C, Wang J, Hsu A Y, et al. Estimation of bare surface soil moisture and surface roughness parameter using L-band SAR image data[J]. IEEE Transactions on Geoseience and Remote Sensing, 1997, 35(5): 1254-1266.

[24] Niclos R, Rivas R, Garcia-Santos V, et al. SMOS level-2 soil moisture product evaluation in rain-fed croplands of the pampean region of Argentina[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(1): 499-512.

[25] Dobson M C, Ulaby F T, Hallikainen M T. Microwave dielectric behavior of wet soil Part II: Dielectric mixing models[J]. IEEE Trans Geosci Remote Sensing, 1985, GE-23(1): 35-46.

[26] Chandravati Prajapati, Nirmal K Viswanathan. Observation of diffractive-correction and spin-orbit interaction induced effects around the Brewster angle[J]. Journal of Optics, 2019, 21(8): 2040-8986.

Inversion of soil moisture based on Brewster angle of soil microwave radiation

Ma Hongzhang1, Ai Lu1, Liu Sumei1, Sun Genyun2, Sun Lin3

(1.,,266580,; 2.,,266580,; 3.,,266590,)

Soil moisture plays a major role in the water and energy budgets of continental surfaces. In the inversion of soil moisture using passive microwave remote sensing technology, soil roughness is the most critical factor restricting the accuracy of the inversion algorithm. Multi-angle remote sensing data has certain advantages in obtaining surface roughness information. Therefore, multi-angle passive microwave observation data has greater application potential in soil moisture inversion. At present, there are few studies on how to use multi-angle passive microwave data to reduce the effect of roughness on soil moisture inversion. Therefore, this study explored the application method of multi-angle passive microwave remote sensing data in soil moisture inversion by analyzing the multi-angle simulated data of soil microwave emissivity. In this study, the Advanced Integral Equation Model (AIEM) was used to simulate the multi-angle microwave radiation of the soil with different Soil Moisture Content (SMC) and roughness. The Brewster angle was calculated based on the trend of the V polarized emissivity with observation angle. The calculation results of Brewster angle showed that Brewster angles of soils with different moisture content distributed in the range of 60°-80°. Based on analysis of the simulated data, Brewster angle had a good consistency with SMC while Brewster angle was not sensitive to parameters such as soil temperature, soil bulk density, and soil roughness. The Brewster angle would change by 15° with SMC changed from 0.05 cm3/cm3to 0.40 cm3/cm3. When the root mean square height of soil roughness increased from 0.5 cm to 3.5 cm, the Brewster angle value increased with the increase of roughness, but the maximum change in angle did not exceed 2°. When the bulk density of the soil changed from 0.9 g/cm3to 1.4 g/cm3, the Brewster angle value increased by no more than 1°. The soil temperature changed from 10 ℃ to 35 ℃, and the Brewster angle changed with the increase of soil temperature. When the root mean square height of the soil roughness and the soil bulk density were combined with different values, the maximum change of Brewster angle did not exceed 2°. This showed that the total influence of soil roughness and soil bulk density on Brewster angle had no obvious accumulation of errors. This study presented an algorithm for inversion of SMC by using the Brewster angle information of soil microwave radiation. Through the analysis of simulated data, a good linear relationship between the tangent value of Brewster angle and SMC was found. The regression results based on simulated data showed that the coefficient of linear fitness between the tangent of Brewster angle and SMC was 0.94, and the root mean square error was 0.027 cm3/cm3. The verification results based on simulated data showed that the coefficient of determination between predicted value of SMC and theoretical value was 0.95, and the root mean square error was 0.024 cm3/cm3. The inversion algorithm proposed here had robust characteristics for different types of soil roughness autocorrelation functions. The prediction accuracy of the algorithm for SMC was little affected by the roughness autocorrelation functions. For different types of roughness autocorrelation functions, the root mean square error between the predicted value of SMC and the theoretical value was 0.023-0.027 cm3/cm3. The SMC inversion algorithm based on Brewster angle utilized the relative change of multi-angle soil emissivity rather than its absolute value and this research provided a novel research idea for the inversion of SMC by using multi-angle passive microwave remote sensing data.

soils; moisture; remote sensing; soil roughness; passive microwave radiation; Brewster angle

马红章，艾璐，刘素美，等. 基于土壤微波辐射布儒斯特角反演土壤含水率[J]. 农业工程学报，2020，36(14)：182-187.doi：10.11975/j.issn.1002-6819.2020.14.022 http://www.tcsae.org

Ma Hongzhang，Ai Lu，Liu Sumei, et al. Inversion of soil moisture based on Brewster angle of soil microwave radiation[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2020, 36(14): 182-187. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2020.14.022 http://www.tcsae.org

2020-02-22

2020-06-10

国家自然科学基金项目（41971292）；山东省自然科学基金项目（ZR2017MD007、ZR2018BD007）

马红章，博士，副教授，主要从事多源遥感辐射传输建模与数据协同机理研究。Email：mahzh@upc.edu.cn

10.11975/j.issn.1002-6819.2020.14.022

TP722.6；S152.7

A

1002-6819(2020)-14-0182-06