基于特征值分析法的双馈风机传动链扭振分析

王晓夫，陈振江，杨林清，李猛，何政宇，龚晟，周洋，张剑波

（云南电网有限责任公司昆明供电局，昆明 650200）

0 前言

人类社会能源危机日益严重，以风力发电为代表的新能源产业随之迅速发展。现代较为完整的风电机组系统如图1 所示，风能经过风力机进入到传动链当中，此时风能转换为机械能，经过发电机使得机械能转换为电能，通过电力电子设备对风电机组达到一些控制目的，最终输出稳定且质量合格的电能并入电网。

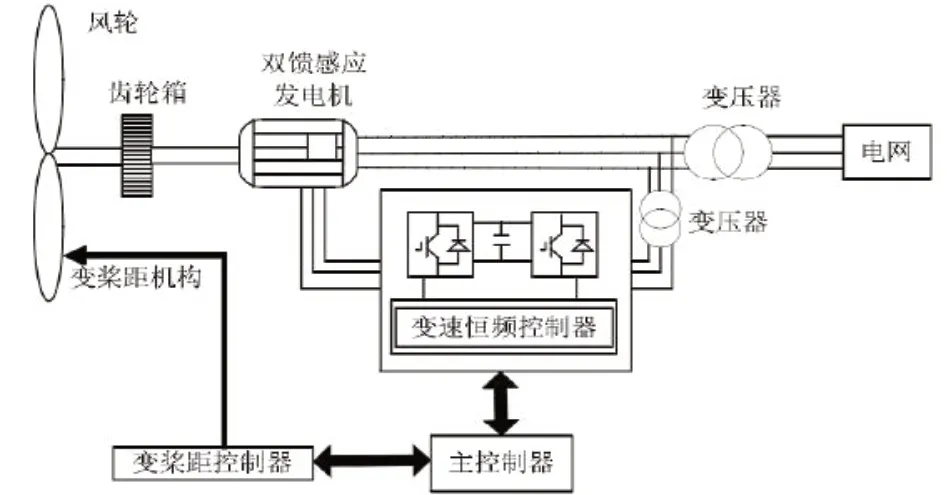
图1 双馈风电机组结构图

双馈风力发电机（DFIG）因其具有最大功率追踪、有功和无功功率的灵活控制、对不确定风速适应性高等优点，成为了风力发电的主力机型。双馈风电机组在运行过程中会因风速变化在轴系上产生交变扭矩从而引起风电机组扭振。如今，风力发电机组发展呈现出单机容量增大、系统柔性不断增加的趋势，大大增加了风电机组发生扭振的可能性，扭振会使得风电机组运行寿命大大减短，严重的甚至会直接造成风电机组损坏，从而大大影响实际的风力发电生产活动，因此对于随机风下风电机组扭振特性的研究显得尤为重要。

1 双馈风电机组传动链建模的研究现状

双馈风电机组的传动链是完成能量传递与能量转换的重要部分，也是风电机组当中最为复杂的部分，传动链中主要部件有风轮、轮毂、低速轴、齿轮箱、高速轴、刹车、联轴器等部分。

目前建立风电机组轴系传动链模型的主要方法是等效质量法，不同的等效情况把传动链等效为不同质量块个数的模型。目前轴系的集中质量模型主要有六质块、四质块、三质块、两质块和单质块模型，风电机组传动链建模的质量块越多，仿真精度越高，但是因为其变量和参数过多，会严重影响仿真的速度，因此在研究扭振特性时一般不使用。两质块的模型并不适合暂态情况的研究，特别是扭振，简化的模型会使得系统丢失某一振荡模态，相比之下三质块模型则能更全面的考虑全部振荡模态，能很好满足扭振特性研究的需要。

本文构建了三质量块的双馈风电机组传动链模型，三个质量块分别为风力机、齿轮箱和发电机，质量块之间以低速轴和高速轴连接，该模型充分考虑传动轴扭转柔性因素部分，根据此模型完成基于特征值分析法的双馈风电机组传动链扭振模态分析。

2 特征值分析法概述

2.1 小干扰分析法理论

李雅普诺夫稳定性定理指出，当一个非线性的系统在某些小扰动的情况下依然可以保持稳定，此时该系统的性质接近线性化系统的性质。因此，可以采用线性化系统的稳定性来研究现实中庞大非线性系统的小干扰稳定性。而实际中的电力系统是一个涉及了多种动态元件的一个复杂非线性系统，对于一个非线性系统，其动态特性的数学模型可用式（1）表示：

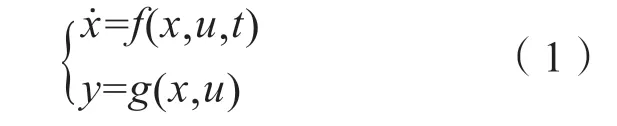
式中，x 为状态变量；u 为系统的输入变量；t 为时间；y 为系统的输出变量。

系统研究需在线性条件下进行，线性化后的系统状态空间方程为：

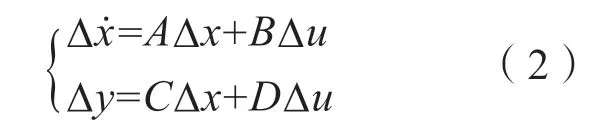
式中A,B,C,D 为该系统在稳态运行点的雅克比矩阵，具体如式（3）到式（6）所示，其中A 为该系统的状态系数矩阵。

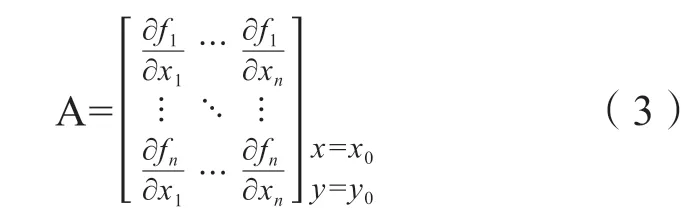
2.2 模态分析法理论

通过小干扰分析法得到系统的状态系数矩阵A，对其使用模态分析法，可得系统状态矩阵的模态情况。主要的求解量有：

2.2.1 系统特征值

状态系数矩阵A 的特征值可以根据下式方程得到：

该方程称为矩阵A 的特征方程，满足该特征方程的就是矩阵A 的特征值。通常情况下，矩阵A 为一个n×n 的矩阵，特征值就分别有λ1,λ2,…,λn。假设特征值为λ=σ+jω，则不同实部和虚部代表着以下不同情况：

1）如果ω=0，此时特征值对应的是非振荡的模态。在此种情况之下，如果σ＞0，那么则表示该模态是非周期发散的，发散速度与σ 绝对值成正比，系统不稳定；如果σ＜0，表示该模态随时间是衰减的，衰减速度与σ 绝对值成正比，最终系统是稳定的。

2）如果ω ≠0，特征根以共轭复数的形式出现，每一对共轭复数对应着一种振荡模态。特征根实部σ 代表的是阻尼大小，如果实部为正值，那么求解特征值的系统对于该模态有正阻尼作用，如果实部为负值，则系统对于该模态起负阻尼作用，此状态下振荡是不收敛的。由ω 可以求出系统的振荡频率f，f=ω⁄2π。

2.2.2 特征向量

对于某一特征值λi，有向量Ui满足方程：

那么，称Ui为矩阵A 关于特征值λi的右特征向量。

同样的，如果有向量Vi满足：

那么，称Vi为矩阵A 关于特征值λi的左特征向量。一般情况下，我们取，这种左特征向量取法称为规格化取法，由此得出，

2.2.3 阻尼比

阻尼比（D）表示模态振荡衰减速度。当D＞0 时，该模态对应的振荡是衰减的，并且阻尼比越大，衰减的速度越快，系统也更早稳定。当D＜0 时，该模态下振荡是不收敛的，并且阻尼比的绝对值越大，振荡的发散速度越快。

2.2.4 相关因子

定义量度第K 个状态量xk和第i 个特征根的相关因子pki为：

Uki、Vki分别为右、左特征向量中第K 行、第i 列的元素，在规格化取法之下，由左右特征向量的运算关系可得：，因此可以将相关因子的计算简化为：

由此可以总结得出，相关因子的值越大，说明状态量xk对于系统该模态的贡献是最大的。根据相关因子，我们能分析得到系统某一模态特征根的主导因素其中的状态变量，为进一步研究扭振提供理论依据。

3 双馈风电机组传动链的模态分析模型

3.1 轴系运动方程

根据轴系集中质量扭振模型模化的方法，综合研究内容的需要以及精度需求，将对双馈风电机组的传动链构建一个三质量块的集中质量模型。如图2 所示。

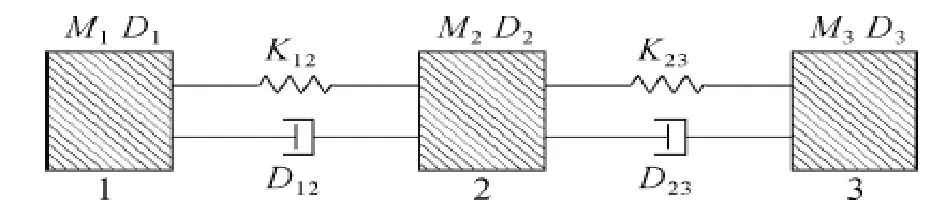
图2 风电机组传动链三质块模型

图中三个质量块1,2,3 分别表示风力机、齿轮箱和发电机转子。M 表示转动惯量，D 表示自阻尼，K12 和K23 为低速轴和高速轴的刚度系数，D12 和D23 表示质量块之间的互阻尼。将风力机低速侧的各量折算到高速侧，并且转换为标幺值，该模型的动力学方程为：

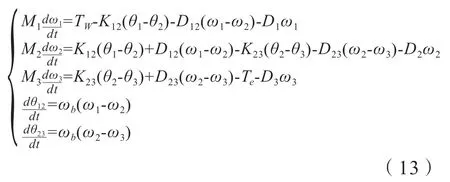
式中，ω1、ω2、ω3表示各质量块的机械角速度；θ1、θ2、θ3表示各质量块的机械转角；TW为风力机的机械转矩；Te为发电机的电磁转矩；ωb为系统电角速度基值，ωb=2πfn。

3.2 轴系标准状态方程

利用小干扰分析法，将上述动力学方程（13）进行线性化，得到线性化之后的系统动力学方程：

根据轴系的标准状态空间模型：

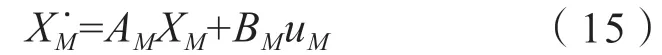
可以得到系统系数矩阵AM，并可据此进行模态分析：

4 双馈风电机组传动链模态分析结果

4.1 传动链扭振模态

表1 中给出的是国内一款常用的双馈风电机组固有参数具体数值，在传动链三质块模型中，将所有量转换为标幺值以后，各部分参数如表所示。

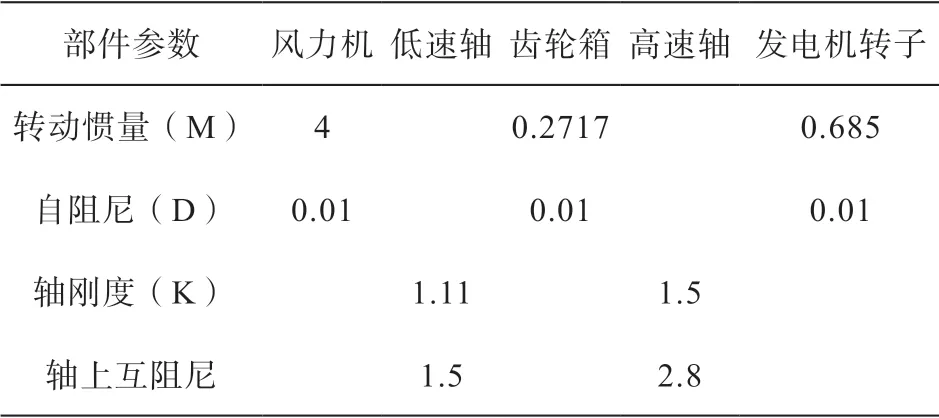
表1 轴系模型参数

所以根据以上参数，可以得出双馈风电机组传动链系统的系数矩阵为：

对系统系数矩阵使用模态分析法，得到的信息如下表所示。

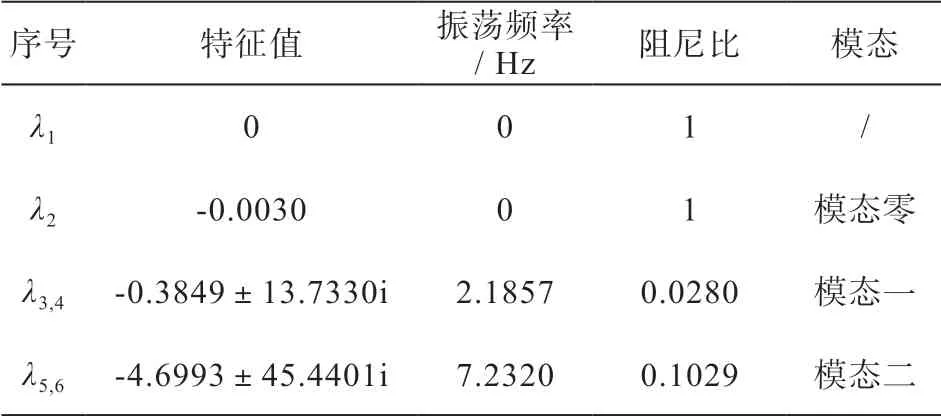
表2 双馈风电机组轴系扭振模态

从上表当中可以得到，这组参数对应的双馈风电机组传动链模型共有三个模态，对应的振荡频率分别为0 Hz、2.1850 Hz 和7.2320 Hz，对应的阻尼比为1，0.0280 和0.1029。从特征值上来看，模态零特征值为0，此模态为非振荡模态；模态一的特征值，实部为负且虚部不等于0，从而可知系统对该振荡模态起到了正阻尼作用；模态二的特征值性质和模态一的相同。

4.2 各模态对应的振型

由每个模态的特征值对应的特征向量可以得到传动链的振型，图中横纵坐标无实际意义，仅为了规划传动链扭振的域，曲线与纵坐标零线的交点为扭振强烈点。如下图3、图4、图5分别给出了三质块传动链模型的振型情况。

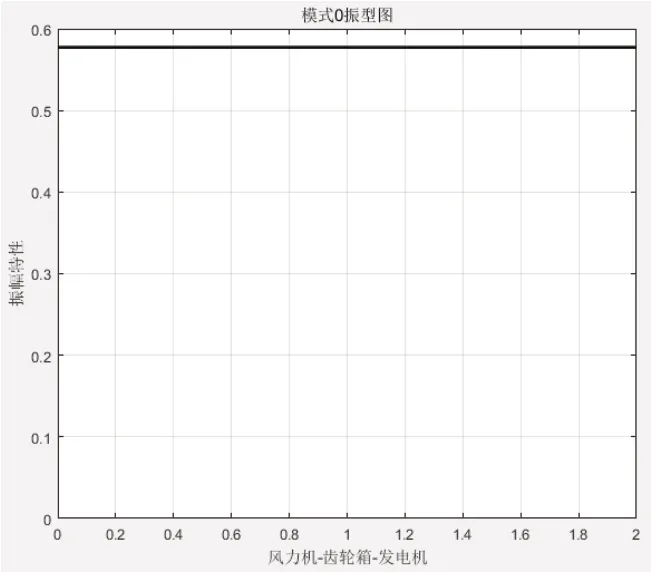
图3 模态零振型图

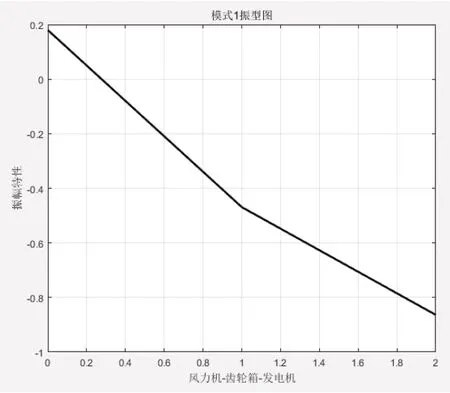
图4 模态一振型图

图5 模态二振型图

从以上振型图，可以看出：

1）模态0 时，扭转频率为0 Hz，此时三个质量块的相对旋转位置大致相等，此时的传动链相对是稳定的，能在双馈风电系统中稳定运行，系统不会发生振荡。

2）模态1 时，扭转频率为2.1857 Hz，振型经过了一次反向,与横轴有一个交点，当扭振模态被激励的时候，齿轮箱和发电机相对风力机振荡，并且发电机的振动幅度最大。

3）模态2 时，扭转频率为7.2320 Hz，振型经过了两次反向，与横轴有两个交点，当扭振模态被激励的时候，风力机和发电机相对于齿轮箱振荡，并且齿轮箱出振动幅度最大。

4.3 参与因子

根据系数矩阵AM，求其左、右特征向量，最终可以得到表示状态变量与各模态相关程度的参与因子。表3 为参与因子计算结果。

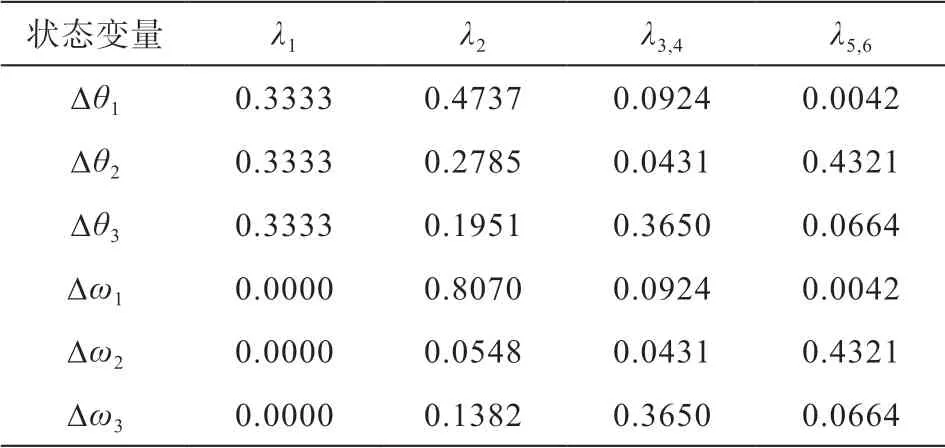
表3 各模态的参与因子

通过参与因子表可以看出，模态0 的情况下，当特征根为λ1时，三个质量块各自的角位移对与该状态的贡献程度一样大；当特征根为λ2时，对于该状态贡献最大的是风力机的转速，其次是风力机的角位移。模态1 的情况下，对于该模态1，发电机转子的角位移和转速的参与程度是最高的，对系统的振荡起到了最大的影响。在模态2 的情况下，齿轮箱的角位移和转速的参与程度是最高的，对系统的振荡起到了最大的影响。由此可知，在无振荡的模态中，风力机的影响作用是最大的；在振荡的模态中，齿轮箱和发电机对于传动链的影响是最大的。

5 结束语

通过建立双馈风电机组传动链的三质块集中质量模型，列写该传动链模型的动力学方程组，运用小干扰分析法对该方程组线性化，得到轴系传动链的标准空间状态模型，以轴系系数矩阵作为轴系的模态分析模型，对双馈风电机组的轴系进行模态分析，对传动链空间状态模型的系数矩阵使用模态分析方法，得到其特征值、特征向量、振荡频率、振型、阻尼比和参与因子等扭振分析信息。

通过模态分析证明特征值分析法在风电机组传动链扭振特性的研究中具有较强的实用性和可靠性，可根据特征值分析法初步确定扭振发生时传动链中振幅较大的部位以及造成振荡的主要参与因素，有助于后续进一步开展风电机组多质量块模型扭振研究，对研究风电场的暂态稳定性提供了一定的模型分析基础。