基于机器人视觉识别的防震锤智能运维研究

蔡晓斌，刘荣海，杨发，郑欣，郭新良，杨迎春，虞鸿江

（云南电网有限责任公司电力科学研究院，昆明 650217）

0 前言

在高压输电线路上，为减轻线路因风力作用而产生的振动，在靠近绝缘子两侧的线路上会安装一定数量的防震锤。但由于输电线路长期暴露在室外环境下，受到光照、雨水等气象条件的影响，防震锤会逐渐受损、甚至失效，而防震锤螺栓松动是导致防震锤失效的主要原因之一。为完成对防震锤螺栓检修，传统方法要求工作人员攀登上杆塔逐个对防震锤完成检修，这种方法劳动强度大、效率低，并且由于高压输电线路有很多架设在人烟稀少的地区，环境较为恶劣[1-2]。随着智能电网建设的逐步推进，国内许多科研单位都开始研制在架空线路上工作的带电作业机器人。1999 年，山东电力研究院、山东鲁能智能技术公司和济宁电业局合作研制了我国首台带电作业机器人[3]，该机器人需要借助于车载平台，不利于在复杂环境下使用。2006 年，武汉大学设计了一款具有越障功能的摆臂式两臂带电作业机器人[4]，该机器人通过两个行走臂直接与输电线路接触实现远程巡检功能。

防震锤和螺栓的识别以及螺栓中心点的提取是带电作业机器人完成防震锤检修工作的两个重要步骤，长沙理工大学的研究团队[5]提出使用卷积神经元网络对架空线路上的物体进行识别，该方法识别准确率高但训练时需要大量的较为准确图片训练集和较多的计算资源，这使得该识别模型更新较为困难，不利于实际运用。以下首先分析了带电作业机器人与螺栓紧固装置的结构需求，基于带电作业机器人在作业时所要识别的物体种类较少、背景较为单一的特点，采用支持向量机方法实现防震锤和螺栓的识别。支持向量机是一种借助于核函数解决非线性分类问题的机器学习方法，由Vapnik[6]提出。对于螺栓中心点的提取，本文分别采用了Hough 变换法和中心矩法进行了对比实验，实验结果表明Hough 变换法更适合于带电作业机器人使用。

1 带电作业机器人螺栓紧固

带电作业机器人需在高压输电线路上完成越障、防振锤螺栓紧固任务，其机械结构应满足以下要求：

1）当输电线路受风力的影响出现晃动时，带电作业机器人应能够在线路上平稳运行；

2）机器人本体机械机构应尽量紧凑以满足在不同线路上运行需求；

3）机器人的行走机构满足一定的爬坡需求；

4）机械臂的运动应避免与导线直接相碰，并且应保证不使机器人重心偏移量过大而导致失衡；

5）螺栓紧固检修臂的套筒应能够更换以适应不同型号的螺栓。

2 防震锤与螺栓识别

带电作业机器人在巡检过程中，安装在机器人上的摄像头会实时捕捉输电线路上的物体，此时需要机器人实时完成对所采集到的图像中的目标进行识别。关于图像识别，在机器视觉中有许多方法。传统的图像识别方法，如基于灰度的匹配方法、基于特征的匹配方法等，其对图像质量要求较高，且鲁棒性较差，不适合用于工作在户外高空环境下的带电作业机器人[5]。本文采用支持向量机（SVM）算法对所采集的防震锤和螺栓图片进行识别，SVM 是一种新的机器学习算法。相较于经典的神经元网络模型，由于机器人所拍摄的图片背景为天空，较为单一，SVM 算法所需的训练样本更少，模型训练耗时小，识别效率高，更适合于带电作业机器人[7]。

2.1 支持向量机原理

在求解非线性问题时，支持向量机可以在高维空间中将非线性问题转化为线性问题，并采用核函数来代替高维空间中复杂内积的计算。SVM 作为一种通用的机器学习方法，最初被用来解决分类问题。SVM 的核心思想可以概括为两点：

1）在线性不可分的情况下，SVM 利用非线性映射将低维空间中的样本映射到高维空间，使之在高维空间中线性可分。

2）基于结构风险最小化理论，SVM 在高维特征空间中构造最优分类超平面，得到分类器的全局最优解。

分类问题通常可以描述为将几个不同元素的正确分离过程，一般可以归结为二分类问题，如图1 所示，圆和星代表两类不同的元素，通过画一条直线来将这两类元素分离，这是一个典型的二分类问题。

图1 二分类问题

如果用SVM 思想来对图1 中的两类元素进行分类，可将分类边界表示为：

式中，ω 和b 是函数的回归参数向量，φ（x）是一个非线性函数，它将向量x 映射到一个高维特征空间。

在空间中可以有无数条分类边界f(x) 将这两类元素分离，SVM 分类器的目的就是寻找一个最优的分类曲面f(x)，使它不仅能正确地划分这两类元素，而且能最大化这两类元素之间的分类间隔，使D 最大。式（1）中参数ω 和b可通过最小化以下正则风险函数来估计。

式（3）中，||ω||2称为正则项，通过最小化||ω||2将使最优分类平面尽可能平坦，从而起到控制函数容量的作用。称为经验误差，由不敏感损失函数Lε(yi,f(xi)) 确定，不敏感损失函数使得SVM 算法将允许分类点到最优分类平面存在最大ε的误差。C为正则化系数。

为了使该方法鲁棒性更好并解决上述优化问题中的一些少量不可行约束，引入松弛变量ξ*i和ξi，将式（3）改写为：

通过引入拉格朗日乘子并利用最优性约束，SVM 函数（1）可改写为以下显式形式：

SVM 算法通常采用核函数来解决非线性特征空间映射问题。径向基函数（Radial Basis Function, RBF）核函数由于其具有较高的计算效率，是各种核函数中应用最为广泛的一种，此外，RBF 核可以将每个样本点映射到一个无穷维特征空间，使得线性不可分的数据线性可分[8]。本文采用RBF 核函数构造SVM 算法。RBF 核函数如下式所示：

式中，γ为核函数参数。

2.2 最优参数搜索

SVM 算法模型和其核函数中有部分参数需要人为设置，一般需要研究者们根据经验设置或通过算法自动寻参，对于这些参数的设置本文将采用网格法进行遍寻，同时用S 折交叉验证（S-Folder Cross Validation）的方法找到最佳参数[9]。具体步骤如下：

1）设定所寻参数某一初始取值范围，和搜索步长；

2）将参数取值范围按搜索步长进行网格划分；

3）将某一参数按网格从大到小将数值带入模型，其余参数不变，利用5 折交叉验证计算误差，即将训练集分为5 份，分别将每一份作为测试样本其余4 份作为训练样本输入模型进行分类，将分类结果与测试样本求误差，预测5次，将5 次误差取平均作为这组参数对应的误差；

4）若存在两组参数所对应的误差小于1×10-4则选择其中风险系数C较小的一组，否则选择误差最小的一组对应参数；

5）将另一个参数按步长减小一次重复步骤（3）和步骤（4）直至所有参数组合都进行过尝试最终选择误差最小的一组对应参数。

步骤4）中本文寻找风险系数C较小的一组参数理由是，C影响模型的学习精度，C的提高会使模型学习精度提高，但模型的泛化能力变差且运算耗时增加，在测试集的拟合效果会明显差于训练集，即过拟合现象。

2.3 图像识别实验

和深度学习算法相比，SVM 算法在进行图片分类时，原始图像信息需先经过特征提取再输入模型进行训练或识别，如图2 所示。本文将采用方向梯度直方图（Histogram of Gradient，HOG）[10]和灰度共生矩阵（Graylevel Co-occurrence Matrix，GLCM）[11]作为输入SVM 算法的图像特征。SVM 算法进行图像识别流程图如下所示：

图2 SVM算法进行图像识别流程图

为检验本文所构建的SVM 算法对架空线路上防震锤与螺栓的识别效果，本文采用防震锤和螺栓实物照片各20 张作为训练集，再分别采用各20 张作为测试集来测试模型的识别率。同时，为进一步验证模型的鲁棒性，本文在测试集中额外增加了输电线路上常见的液压线夹和绝缘子各10 张，最终测试集图像数量为60。测试结果如下表所示：

表1 识别测试结果

带电作业机器人在执行巡检任务时，机器人的摄像头会对输电线路上的物体进行实时检测，同一物体将被多次识别，根据表1 识别测试结果，本文所构建的基于SVM 的识别模型能够满足作业需求。

3 螺栓中心点提取

在机器人执行防震锤自主检修任务时，需要安装在维修机械臂上的摄像头设备螺栓并提取中心点。要使螺栓紧固机构正确完成任务则要求螺栓中心点提取精度足够高。为寻找一个合适中心点提取方法，本文将使用中心矩法和Hough 变换法分别对螺栓实物图像的中心点进行提取实验，并通过计算提取结果的标准差来比较两种方法的效果。

标准差计算公式如下：

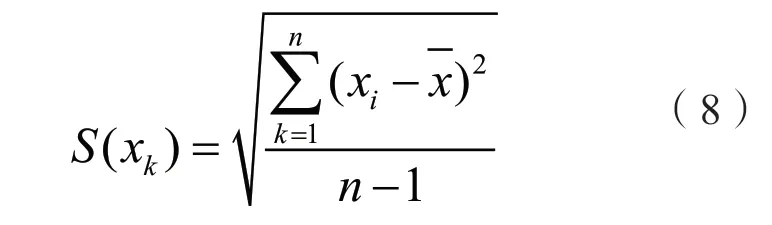
式中，xi为计算中心点x 轴或y 轴像素坐标，为xi的平均值。

在对螺栓中心点进行提取之前，需对螺栓灰度图像进行二值化处理[12]，本文采用自适应二值化方法对螺栓灰度图像进行处理，处理效果如图3 所示。

图3 二值化效果图

3.1 中心矩法

中心矩法通过计算物体在图像上的质心来确定其中心点。中心矩法具有计算速度快，算法简单的特点。尤其在光斑光强比较均匀、对称性好的情况时效果更加突出。但是只能检测光斑中心、不能检测半径。要计算二值化后图像的质心需先计算图像零阶矩m00、一阶矩m10、二阶矩m01：

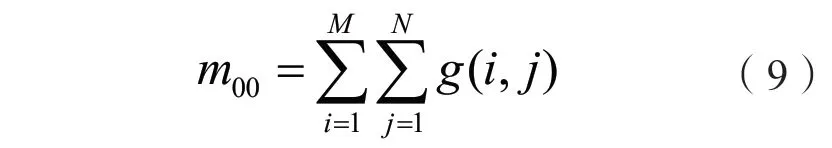
式中，当图像像素点为亮点时g(i, j)=1，当图像像素点为暗点时g(i, j)=0。

中心位置坐标由下式计算：

3.2 Hough变换法

Hough 变 换 是 由Paul Hough 于1962 年 提出的一种检测圆的算法，它是一种基于累加器的投票机制用来检测圆特征的算法，具有精度高，抗干扰能力强等优点[13]。它的基本思想是：将原始图像从原图像空间变换到参数空间，并在参数空间中使用大多数边界点都满足的某种参数形式作为图像中的曲线的描述，再通过设置累加器对参数进行累积，其峰值对应的点就是所需要的信息。

对于一个如式（13）描述的圆，Hough 变换先对原始灰度图像进行边缘检测，理想情况下，对像素空间的一个点(x,y)，其在三维参数空间(a,b,r) 中对应一个圆锥；而像素空间的一个圆就对应着这三维参数空间中一簇圆锥。这一簇圆锥将相交于一个点，当这个点的三维参数一定，就能找到其所对于的像素空间中的圆，Hough 变换提取圆心原理如图4 所示。

图4 Hough变换提取圆心原理

3.3 螺栓中心点提取实验

为了对比中心矩法和Hough 变换法用于提取螺栓中心的效果，本文利用图3 所示的螺栓图片进行对比实验，原始灰度图片会先经过二值化处理，再使用加入均值为0、方差为25 的高斯白噪声，具体实验流程如下图所示：

图5 实验流程

中心矩法和Hough 变换法都将进行100 次独立实验，最终实验结果如下表所示：

表2 中心点提取实验结果

如表2 所示，采用Hough 变换法提取螺栓中心点在x轴和y轴标准差均更小，这说明Hough 变换法对于螺栓中心点的提取更稳定。

根据本文的实验结果，Hough 变换法相较于中心矩法更适合于带电作业机器人防震锤检修过程中用于提取螺栓中心位置。且由于螺栓松动，螺栓中心轴与防震锤螺栓安装表面会存在一定的倾角，这时相机拍摄的螺栓图像会出现倾斜，此时采用中心矩法求螺栓中心时需对相机角度进行修正，不利于带电作业机器人实际操作。

4 结束语

本文主要研究了带电作业机器人在防震锤检修过程中对防震锤和螺栓的识别，以及螺栓中心点的提取过程。防震锤在抵抗高压输电线路因风力作用而产生振动过程中发挥着重要作用，而螺栓的松动是防震锤失效的主要原因之一。为了能够高效识别出架空导线上的防震锤与螺栓，本文利用基于径向基函数所构造支持向量机对所采集的防震锤、螺栓、线夹和绝缘子图像进行识别实验，实验结果表明，该方法能够在训练样本较少的情况下有效满足带电作业机器人在高压架空线路环境下的识别任务。

针对螺栓中心点的提取工作，本文分别利用中心矩法和Hough 变换法进行对比实验，实验结果表明Hough 变换法对于带电作业机器人的工作需求是一种更加稳定的方法。

本文的部分研究内容还未完全深入，需要更进一步的研究工作，如支持向量机核函数的选取问题和支持向量机及核函数的参数寻优问题，架空线路带电作业机器人所处的工作环境较为特殊，在这种特殊环境下的相关研究有待进一步深入。