网络攻击环境下的量化反馈控制系统

吉明明

(上海工程技术大学 智能控制与机器人实验室，上海 201620)

网络攻击是指借助各种先进的信息技术，以敌方的信息网络系统为主要目标而发起的攻击，因其成功率高、风险小、代价低、所造成的损失巨大等特点而成为很多攻击者惯用的手段。我国的网络安全系统在预测、反应、防范和恢复能力方面在现阶段还存在许多薄弱环节[1]，因此，加强对网络攻击的研究有助于提高我国的网络威慑力，对捍卫国家安全有着非常重要的意义。

研究人员对如何提高网络控制系统的安全性以及可靠性等极为关注并取得了很多有重要意义的研究成果。为了保证网络控制系统的安全性，相关文献中报道的处理网络攻击的方法主要有2种：第1种方法是采用软件或者硬件工具来检测或辨识所传输的数据是否遭到破坏，一旦发现数据被破坏就抛弃或重发这些数据；第2种方法是设计一个控制系统，使被控系统对恶意攻击是不敏感的或者鲁棒的。本文中主要采用第2种方法，即从控制角度出发来处理网络攻击，关于这方面的研究目前已有一些很有意义的研究成果。例如，文献[2]中假设系统遭受了欺骗攻击，讨论随机非线性系统的安全控制问题，得到了系统依给定概率安全的充分性条件。文献[3]中研究带有欺骗攻击的一类网络化系统的预测控制问题，基于切换系统理论，给出了闭环系统稳定的条件。文献[4]中研究了具有监管和监督控制层的网络控制系统的安全威胁评估问题，以水务的数据采集与监视控制(SCADA)系统为例，指出现有的随机故障诊断工具不足以诊断网络攻击。文献[5]中假设2种不同类型的攻击，对遭受攻击的网络控制系统进行分析，其中一种攻击假设出现在网络节点上，另一种攻击假设出现在通信网络和节点之间，利用观测器提出了一种能够发现和隔离攻击的分布式机制。更多关于网络控制系统的安全性问题的研究可参考文献[6-9]。由以上文献可知，目前关于网络控制系统的网络安全问题的研究大部分都假设信号在网络通道之间进行传输时是无损失的，然而，网络系统的数字性导致该假设几乎是不可能的。对于网络系统，信号在传输之前首先要进行量化，或者由于存在计算误差和舍入误差，系统中的控制器本身有时也存在量化，因此，对遭受攻击的网络控制系统进行量化反馈控制研究很有必要。

量化广泛存在于数字系统中，主要由以下2个方面引起：一方面是控制器本身存在量化，即由有限字长表示引起的计算误差和系数舍入误差；另一方面是反馈控制系统中控制器和被控设备之间传输通道上的信号也存在量化。关于量化的相关研究成果可参考文献[10-20]。量化器的种类有很多，如均匀量化器、对数量化器等。由于对数量化器具有使系统达到稳定所需要的信息更少、所占用的网络带宽也更小等特点，可用于遭受攻击的网络控制系统中传输信号的量化，因此在控制理论中受到很多关注并得到广泛应用。

结合遭受攻击的网络控制系统的研究现状，本文中采用对数量化器研究遭受攻击的网络控制系统的量化反馈控制问题。对遭受网络攻击的系统而言，最核心的问题是必须满足系统的安全性要求，因此，本文中重点在于设计合适的控制器，使得遭受网络攻击的系统是安全的。首先，针对网络攻击的特点，用2组独立同分布的随机变量序列刻画事件发生的任意性与随机性，从而得到一个随机系统；然后根据对数量化器的扇形界性质，将量化反馈控制问题转化为鲁棒控制问题，借助线性矩阵不等式给出判定系统依概率安全的充分条件并得到了相应的控制器的设计方法；最后用一个数值例子验证本文中所提出的方法的有效性。

1 问题描述

考虑遭受网络攻击的离散时间量化反馈控制系统

(1)

式中：x(k)∈nx为系统的状态向量，k∈；ny为传感器测量；y(k)∈ny为控制器实际接收到的信号；nu为控制器输出；u(k)∈nu为执行器输入(以上为实数集，nx、ny、nu均为正整数)；ω(k)、υ(k)分别为由攻击者发出的干扰信号；q(·)为量化器；αk、σk为独立同分布的伯努利随机变量序列。αk、σk的分布律为

P{αk=0}=1-α，P{αk=1}=α，

P{σk=0}=1-σ，P{σk=1}=σ，

式中：P{·}为随机事件发生的概率，0≤α≤1，0≤σ≤1。该系统的控制结构图如图1所示。

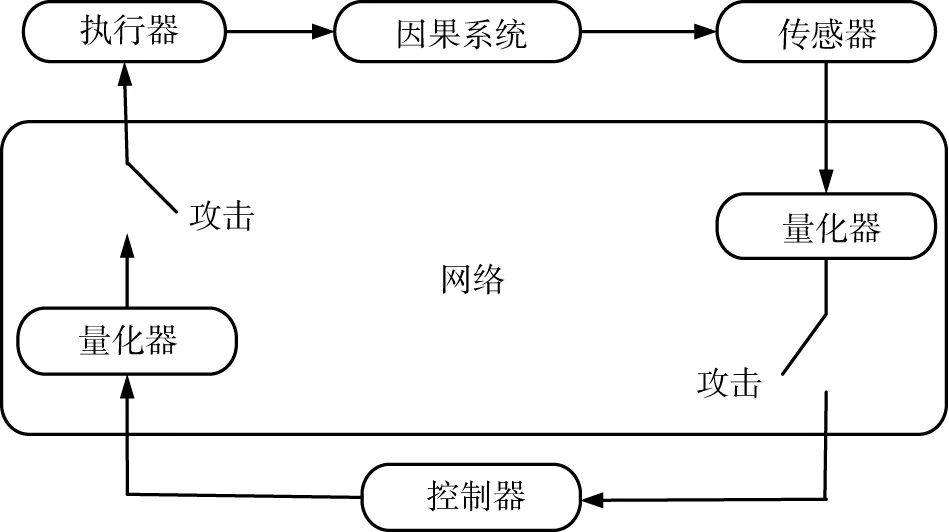
图1 量化反馈控制系统控制结构图

本文中假设q(·)是对数形式的。对数量化器由Elia等[11]提出，是量化反馈控制系统中经常使用的一种静态量化器，因为具有使量化状态反馈的确定性单输入离散时间线性时不变系统二次镇定的最粗糙量化密度，所以深得广大学者的青睐。

若系统的量化信号v(k)为

v(k)=(v1(k)v2(k)…vr(k))T，

则q(·)的定义为

q[v(k)]=(q1[v1(k)]q2[v2(k)]…qr[vr(k)])T。

对于任一分量qj(·)(j=1,2,…,r)，量化层数为

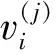
(2)

由文献[12]可知，对数量化器满足扇形界性质，即

qj[vj(k)]=(1+Δj)vj(k),Δj≤τj(j=1,2,…,r),令Δ=diag(Δ1,Δ2, …,Δr)，则

q[v(k)]=(I+Δ)v(k)，

(3)

式中：Δ为对角矩阵；I为单位矩阵。

对于遭受网络攻击的系统(1)，假设攻击者在阻止正确信息传送的同时向目标对象发送一个虚假信息，即攻击信号ω(k)、υ(k)，分别定义为

(4)

(5)

且

(6)

对于系统(1)，所设计的动态输出反馈控制器为

(7)

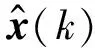
本文中主要目的是为系统(1)设计动态输出反馈控制器(7)，使得系统是依概率安全的。首先给出安全性的定义以及本文中所用到的其他定义及引理。

定义1[2]给定安全参数θ>0以及正标量ε>0，对于系统(1)，若满足

则称系统(1)是依概率1-ε安全的。

定义3[2]对于任意的ε>0、k≥0以及x(0)∈n{0}，如果存在KL类函数和K类函数γ，使得系统(1)满足

则系统(1)是概率输入到状态稳定的。

引理1[2]对于所有的x(k)∈n{0}，如果存在正定函数V∶n→，2个K∞类函数α和以及2个K类函数χ和α，使得不等式

2 方法设计

根据量化器q(·)的扇形界性质，可得

(8)

(9)

则由式(1)、(7)—(9)，可得

αkBζ1(k)，

(10)

σkBcζ2(k)。

(11)

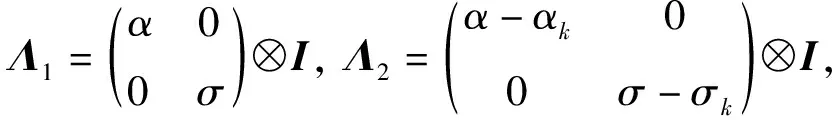
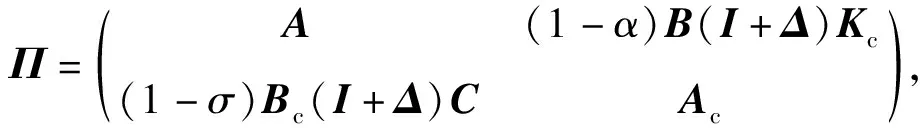
η(k+1)=[Π+(α-αk)Σ+(σ-σk)Γ]η(k)+

(Λ1+Λ2)Ψζ(k)。

(12)

使系统安全的充分条件如定理1所示。

定理1给定ω>0以及控制器参数Ac、Bc、Kc，对于任意非零的η(k)∈2nx，如果存在正定矩阵P以及正标量χ，使得不等式

(1+ω)H-P≤0，

(13)

D≤χI，

(14)

证明：对正定矩阵P，定义李雅普诺夫函数V[η(k)]=ηT(k)Pη(k)，对于闭环系统(12)，有

E{V[η(k+1)]-V[η(k)]}=

E[ηT(k+1)Pη(k+1)-ηT(k)Pη(k)]=

ηT(k)(H-P)η(k)+ζT(k)Dζ(k)+

2ηT(k)[ΠTPΛ1Ψ+α(1-α)ΣTPM1Ψ+

σ(1-σ)ΓTPM2Ψ]ζ(k)。

对于ω>0，由于

2ηT(k)[ΠTPΛ1Ψ+α(1-α)ΣTPM1Ψ+

σ(1-σ)ΓTPM2Ψ]ζ(k)≤ωηT(k)Hη(k)+

ω-1ζT(k)Dζ(k)，

因此，

E{V[η(k+1)]-V[η(k)]}≤

ηT(k)[(1+ω)H-P]η(k)+

(1+ω-1)ζT(k)Dζ(k)。

若式(13)、(14)成立，则

E{V[η(k+1)]-V[η(k)]}≤

式中λmin(·)为相应矩阵的最小特征值。

根据引理1，系统(12)是依概率输入到状态稳定的，则

取x(0)=η(0)，则

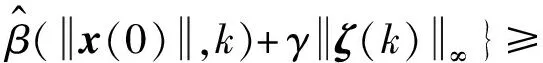
因此，系统(1)是依概率1-ε安全的。定理1证毕。

基于定理1，下面给出使系统(1)依概率安全的控制器(7)的设计方法。

定理2给定ω>0、τ>0，如果存在正定矩阵Q，矩阵U1、U2和U3以及正标量χ，使得线性矩阵不等式

(15)

(16)

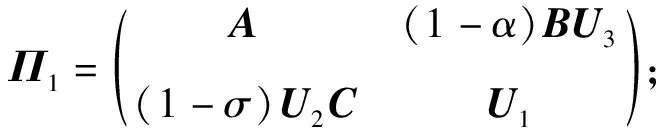
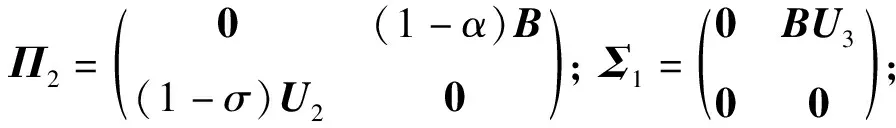
证明：根据Schur补引理，(1+ω)H-P≤0等价于

(17)

令Ac=U1，Bc=U2，Kc=U3，因Π=Π1+Π2ΔΥ，Σ=Σ1+Σ2ΔΥ，Γ=Γ1+Γ2ΔΥ，则式(17)可写成

(18)

根据S-Procedure方法，式(18)成立当且仅当对于τ>0，

(19)

即

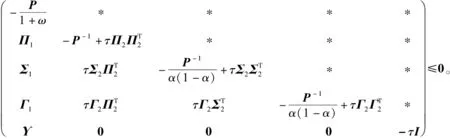
(20)

对于式(20)，令Q=P-1，则有

(21)

式(21)分别左乘及右乘矩阵diag(Q,I,I,I,I)，得

(22)

即式(15)成立。

另一方面，根据Shur补引理，D≤χI等价于

(23)

即式(16)成立。

综上，若式(15)、(16)成立，则系统(1)是依概率1-ε安全的。定理2证毕。

3 实例验证

以下用一个数值例子来验证本文中所得结论的有效性。

根据本文中所得到的定理2的结论，下面设计合适的控制器使得系统是依概率安全的。

借助于MATLAB软件，通过求解线性矩阵不等式(15)、(16)，可以得到使系统依概率安全的动态输出反馈控制器(7)的增益矩阵分别为

Kc=(-0.485 0 -0.187 9)，χ=0.548 0。

x(k)∈nx—系统的状态向量，k∈；矩阵的2范数。

4 结语

根据网络控制系统的数字性、易攻击性等特点，本文中研究了遭受攻击的网络控制系统的量化反馈控制问题。假设传感器和控制器的输出信号被对数量化器量化，根据网络攻击的特点以及对数量化器的扇形界性质，将量化反馈控制问题转化为一个随机不确定性鲁棒控制问题。通过构造李雅普诺夫函数得到了判断该系统依概率安全的充分条件，并在此基础上给出了相应的控制器的设计方法，数值例子验证了该设计方法的有效性。