农村公路传力杆材料性质对传荷影响的研究
农村公路是支撑农村经济发展的重要基础设施,随着我国新农村建设的推进,全国农村基本上实现了村村通车。农村公路主要采用水泥混凝土路面形式,随着农村公路大型货运车辆的出现,超载超限的现象时有发生,加重了农村公路出现错台、翘曲等公路病害问题的几率,且农村公路缺乏养护,一般通车后就疏于管理。
按照传统农村公路的设计标准,路面各混凝土板间相互独立,若是只有小型车辆通行,一般不易引发严重的公路病害,其耐久性也有相应保障,但目前农村公路面临地质地形差异较大、施工大型机械无法进场、质量无法保证、公路横断面窄、超载超限现象加重等方面的问题。为减少水泥混凝土路面在接缝处产生断裂、错台等现象,减少公路养护成本,建议农村公路设置传力杆[1]-[2]。
申俊敏通过建立Winkler 地基上的双层结构模型,分析了传力杆的空间位置以及与混凝土的结合状况对传荷能力的影响[3]。罗勇通过对有限元软件的应用与探索,总结出模拟接缝传荷行为弹簧单元法、虚拟材料层法以及实体建模法三种方法:分别分析了三种方法的优劣势[4]。锁利军通过建立有无传力杆的三维有限元水泥混凝土路面模型,分析了接缝处水泥混凝土面层的荷载应力、弯沉等的差异性[5]。高伟采用布拉德伯利(R.D.Bradbury)传力杆实用设计验算公式和水泥混凝土路面三维有限元分析程序EverFE,对传力杆设置间距进行了探讨[6]。王宇翔通过有限元软件分析接缝传荷行为与试验结果吻合,验证了有限元分析接缝传荷的可行性[7]。
目前,针对传力杆受荷行为的分析,主要以高速公路为原型尺寸,建立有限元模型,而以农村公路尺寸为参照、以路面板边受荷建立接缝传荷有限元分析模型的研究成果不足。本文以成都地区某农村公路为原型,建立板边角受荷,分析传力杆自身材料性质对传荷能力的影响。
1.建立水泥混凝土路面三维有限元模型
1.1 路面结构尺寸
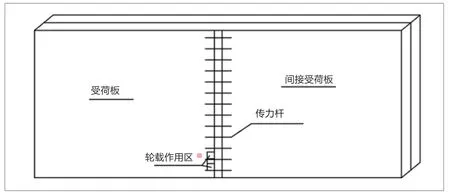
图1 路面结构模型

图2 路面结构有限元模型及其网格划分
本研究结合成都地区某农村公路实际路面结构尺寸,建立路面结构有限元模型,所建路面结构模型单板长5m,两板总长10m,面层厚0.24m、基层厚0.3m,总厚0.54m,道路割缝宽0.01m,横断面宽4m,传力杆基准长度为0.41m、间距0.3m、直径0.01m,总计13根,布设位置为面层板中部。本研究主要考虑混凝土路面板角受荷时路面的力学响应状况,故轮载作用区域为板角处,轮载作用在水泥混凝土路面板中部,作用区域大小为18.6cm×19.6cm,两轮中心距12.8cm,采用BZZ-10,水泥混凝土路面结构及荷载作用位置见图1。
1.2 有限元模型建立
在有限元模拟计算分析过程中,做以下假定:
一是地基采用弹性地基板;
二是水泥混凝土材料为各向同性、连续且均匀的材料;
三是水泥混凝土路面与地基之间的接触为完全连续,无脱空。
在建立水泥混凝土路面模型时,传力杆与水泥混凝土之间采用嵌入约束,约束路面结构XY 方向的位移以及约束传力杆沿X 轴的转动。传力杆采用两结点空间线性梁单元,水泥混凝土采用二十结点二次六面体单元。为保证计算精度与效率,仅对荷载作用区域网格进行精细划分,网格尺寸为3cm×3cm 路面结构有限元模型及网格划分,如图2所示。
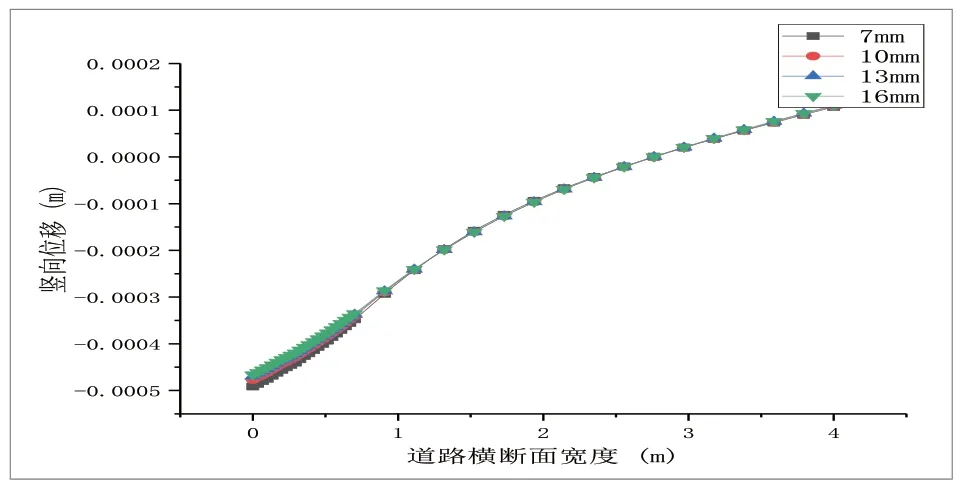
图3 传力杆直径对受荷板层底竖向位移的影响
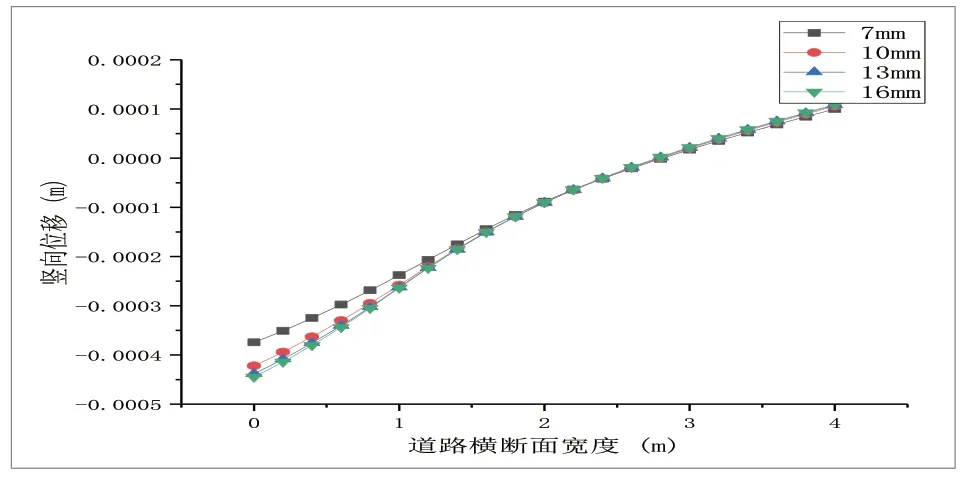
图4 传力杆直径对间接受荷板层底竖向位移的影响

图5 传力杆直径对受荷板层底拉应力的影响
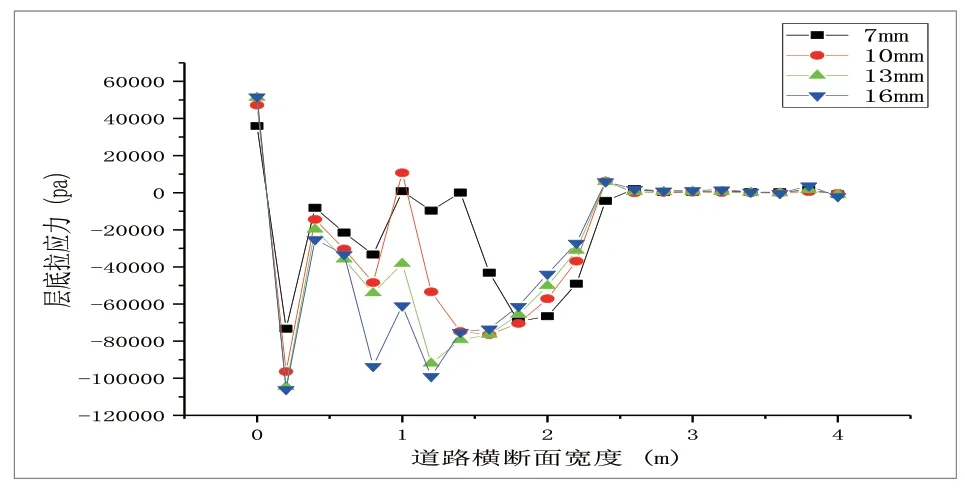
图6 传力杆直径对间接受荷板层底拉应力的影响
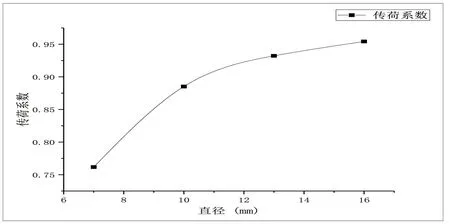
图7 传荷系数随传力杆直径的变化
1.3 接缝传荷能力
水泥混凝土路面在传力杆的作用下,可以实现板间荷载传递,直接受荷板传递给间接受荷板的能力即为接缝传荷能力;接缝两侧所受荷载比即为传荷系数。但是,荷载分配的实际情况难以分析,故提出反应传荷能力的间接方法以及指标:挠度法与应变法。本文采用挠度法及其指标作为传荷能力评价方法。
挠度法,即采用接缝相邻板之间挠度的比值,表征传荷能力即:
Ew=ω1/ω2
式中:Ew——接缝挠度传荷系数
ω1——受荷板挠度值
ω2——间接受荷板挠度值
2.传荷能力影响因素分析
影响接缝传荷能力的因素众多,本研究主要研究传力自身材料参数对传荷能力的影响,其因素主要包括三类:传力杆直径、传力杆长度、传力杆弹性模量。
2.1 直径的影响
设计传力杆直径为7mm、10mm、13mm、16mm 时,根据其受荷板与未受荷板层底在竖向位移以及应力的变化状况,从而研究直径对传力能力的影响。对竖向位移的影响结果,如图3、图4所示。
从图3、图4分析得出,随着传力杆直径从7mm 增长至16mm,直接受荷板侧竖向位移逐渐增加,但增加的幅值很小,约为0.48mm;距离板边沿1m 外,竖向位移无明显差异。间接受荷板侧随传力杆直径的逐渐增加,板角边沿竖向位移逐渐增加,在7mm-10mm 范围内,竖向位移增加明显,其后增加幅值降低,距离板边沿约2m 后竖向位移无明显差异。对层底拉应力的影响,分析结果如图5、图6所示。
从图5、图6分析得出,随着传力杆直径等差增长,直接受荷板侧层底拉应力逐渐降低,在轮载作用区域,其拉应力在轮载中心取得最大值0.102MPa,轮载的影响范围约为2m;在未受荷板侧层底拉应力逐渐增加,影响范围相似。根据接缝传荷系数的公式,传荷系数随直径的变化计算结果如图7所示。
从图7分析得出,随着传力杆直径的增加,接缝传荷系数逐渐增加,增加的幅度随直径增加而逐渐降低。
2.2 传力杆弹性模量的影响
本研究设计了传力杆弹模为100GPa、150GPa、200GPa、250GPa 时,其受荷板与未受荷板层底在竖向位移以及应力的变化状况,从而研究传力杆弹模对传荷力能力的影响。对竖向位移的影响结果,如图8、图9所示。
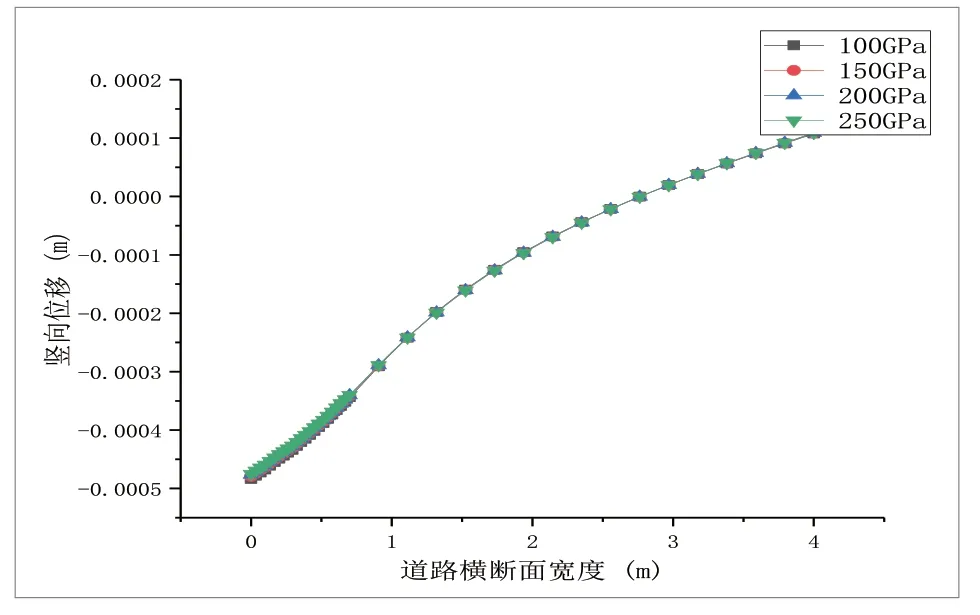
图8 传力杆弹模对受荷板层底竖向位移的影响

图9 传力杆弹模对间接受荷板层底竖向位移的影响

图10 传力杆弹模对受荷板层底拉应力的影响

图11 传力杆弹模对间接受荷板层底拉应力的影响

图12 传荷系数随传力杆弹性模量的变化

图13 传力杆长度对受荷板层底竖向位移的影响
从图8、图9分析得出,随着传力杆弹模从100GPa 增长至200GPa,直接受荷板侧竖向位移略微减小,但减小的幅值很小,约为0.48mm,竖向位移无明显差异。间接受荷板侧随传力杆弹性模量的逐渐增加,板角边沿竖向位移逐渐增加,增加的幅值极小,皆约为0.41mm。对层底拉应力的影响分析结果,如图10、图11所示。
从图10、图11分析得出,随着传力杆弹性模量等差增长,直接受荷板侧层底拉应力逐渐降低,在轮载作用区域,其拉应力在轮载中心取得最大值0.96MPa,轮载的影响范围约为2m;在未受荷板侧层底拉应力逐渐增加,影响范围相似,最大拉应力为0.989MPa。根据接缝传荷系数的公式,传荷系数随直径的变化计算结果如图12所示。
从图12 分析得出,随着传力杆直径的增加,接缝传荷系数逐渐增加,增加的幅度随直径增加而逐渐降低,整体增长幅值从0.82 至0.89,相较于直径带来的影响,弹性的影响更小。
2.3 传力杆长度
本研究设计了传力杆长度为0.41m、0.45m、0.49m、0.53m 时,其受荷板与未受荷板层底在竖向位移以及应力的变化状况,从而研究传力杆长度对传荷力能力的影响。对竖向位移的影响结果,如图13、图14所示。
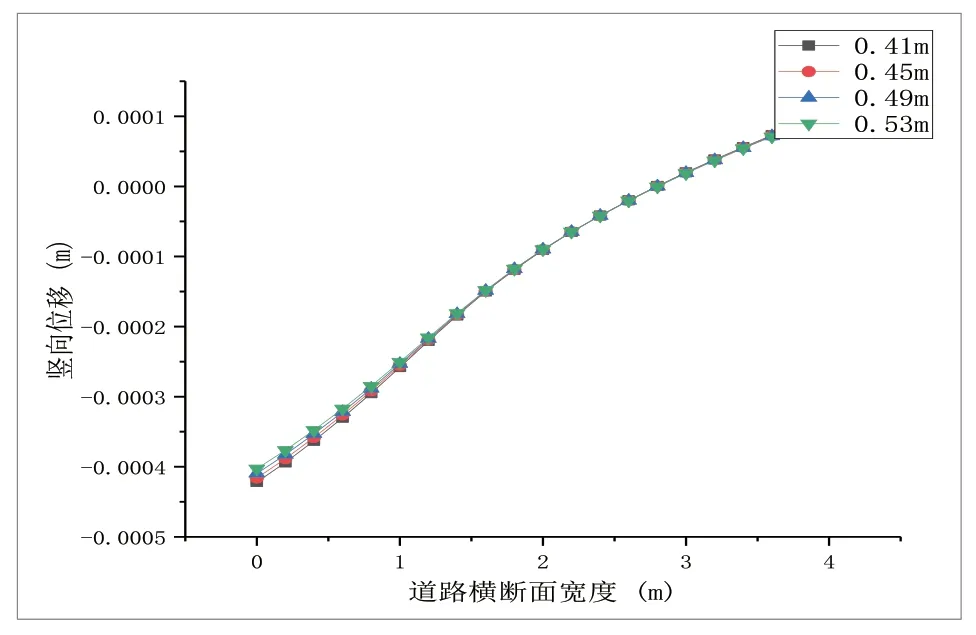
图14 传力杆长度对间接受荷板层底竖向位移的影响

图15 传力杆长度对间接受荷板层底拉应力的影响

图16 传力杆长度对间接受荷板层底拉应力的影响
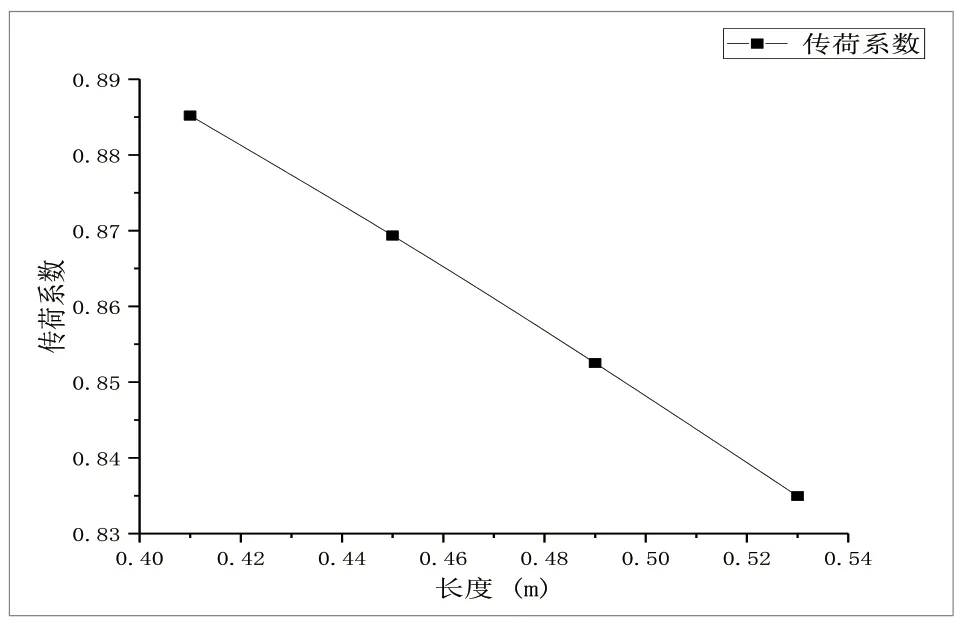
图17 传荷系数随传力杆长度的变化
从图13、图14分析得出,随着传力杆长度从0.41m 增长至0.43m,直接受荷板侧竖向位移逐渐降低,但增加的幅值很小,约0.48mm,竖向位移无明显差异。间接受荷板侧随传力杆长度的增加,板角边沿竖向位移逐渐降低,降低幅值极小,竖向位移无明显差异。对层底拉应力的影响分析结果,如图15、图16所示。
从图15、图16分析得出,随着传力杆长度以0.03m 的等差增长,直接受荷板侧层底拉应力逐渐增加,在轮载作用区域,其拉应力在轮载中心取得最大值0.91MPa;在未受荷板侧层底拉应力逐渐减小,影响范围相似,最大拉应力为0.14MPa,根据接缝传荷系数的公式,传荷系数随直径的变化计算结果如图17所示。
从图17分析得出,随着传力杆长度的增加,接缝传荷系数逐渐降低,且呈线性降低,整体降低数值从0.88至0.83,相较于直径、弹模,传力杆长度的影响更小。
3.结论
本文通过研究传力杆自身材料特性,直径、长度、弹性模量对面层底竖向位移、拉应力以及传荷系数的影响,得出以下结论:
随着传力杆直径增加,直接受荷板与间接受荷板竖向位移皆增加;受荷板层底拉应力逐渐降低,间接受荷板层底竖向位移逐渐增加。
随着传力杆弹性模量增加,直接受荷板竖向位移略微减小,间接受荷板竖向位移增加;受荷板层底拉应力逐渐降低,间接受荷板层底竖向位移逐渐增加。
随着传力长度增加,直接受荷板竖向位移略微减小,间接受荷板竖向位移增加;受荷板层底拉应力逐渐增加,间接受荷板层底竖向位移逐渐减小。
接缝传荷系数随传力杆直径的增加而增加,随弹模增加而增加,随长度的增加而减小。

