网格化GNSS弱干扰源定位方法

刘睿,陈奇东,甄卫民

(中国电波传播研究所,山东 青岛 266107)

0 引 言

全球卫星导航系统(GNSS)为导航带来了革命性的变化,它在全球范围内为无限多的海陆空天用户提供精确的实时位置、速度和时间信息,一旦GNSS受到干扰,就会对与国家安全、国民经济等方面密切相关的关键基础设施造成严重影响和不可预计的后果[1]. GNSS信号落地功率低,约为-13 dBm,同时信号采用扩频体制,其功率谱密度更低,频谱严重地淹没在环境噪声当中,很弱的干扰即可影响GNSS的应用[2].

常用的网格化GNSS干扰源定位方法有波达方向(DOA)定位方法[3],到达时间差(TDOA)定位方法[4]和到达信号强度(RSS)定位方法[5]. 其中TDOA方法以其定位速度快、精度高等特点获得了广泛的推广应用. 目前TDOA通常使用广义互相关算法(GCC)[6]等方法估计接收机间的信号到达时差,然后通过双曲线定位算法解算干扰源位置.

对GNSS弱干扰源定位时,上述方法对信噪比低的情况适应能力较差,针对该问题,本文提出一种基于信号噪声分离的差方均值函数拟合(MFDSS[2])的网格化GNSS弱干扰源定位方法,方法采用MFDSS方法实现时差估计,然后利用Chan[7]双曲线定位算法解算干扰源位置. 同时,本文还介绍了采用上述方法的网格化GNSS弱干扰源定位系统组成,对系统的定位性能进行了仿真与分析并给出结论.

1 网格化GNSS弱干扰源定位系统及接收信号模型

网格化GNSS弱干扰源定位系统的组成框图如图1所示,包含监测接收层、数据传输层和中心处理层三个层次. 监测接收层由网格化监测接收机组成,实现对干扰信号的采集接收并对接收数据打时间标记;数据传输层由4G等无线通信链路实现;中心处理层的数据处理平台收集各接收机数据,通过执行本文方法实现对弱干扰信号的准确定位.

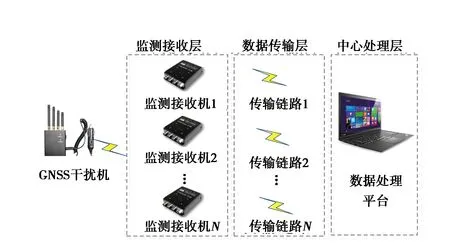
图1 网格化GNSS弱干扰源定位系统的组成框图

存在干扰的情况下,监测接收机接收到的信号包含目标干扰信号s(n)和噪声信号n(n),接收机接收信号模型如式(1),对于目标干扰信号的检测定位,噪声信号n(n)包含隐藏在噪声下的GNSS信号,具有相关性,对时差估计有一定影响.

x(n)=s(n)+n(n).

(1)

2 基于MFDSS的弱干扰源定位方法

2.1 基于MFDSS的时差估计方法

方法利用目标干扰信号与噪声间的正交性采用奇异值差分谱滤除噪声,然后通过拟合方法求出差方均值函数精确的极小值以实现弱干扰的时差估计值.

2.1.1 奇异值差分谱噪声滤除方法

方法首先依据式(1)对接收信号构造Hankel矩阵,x(n)信号长度为N,x(n)的Hankel矩阵表达式如下:

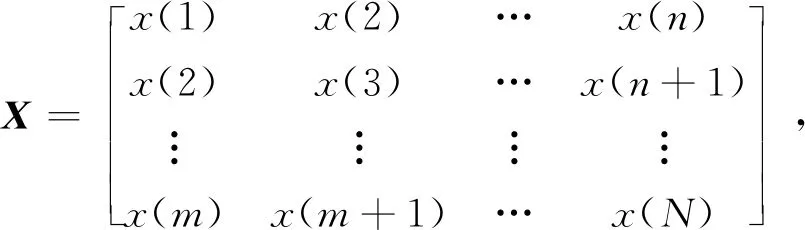
(2)

式中,根据N为偶数和奇数时,m取值分别为N/2和(N+1)/2，n取值分别为N/2+1和(N+1)/2.对矩阵X进行奇异值分解可得式(3):

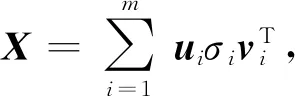
(3)

式中：ui为m维列向量；σi为矩阵X的奇异值；vi为n维列向量,分解后σi由大到小排列并利用式(4)构造奇异值差分谱b=(b1,b2,…,bm-1),其中bi的表达式为

bi=σi-σi+1,i=1,2,…，m-1.

(4)

方法通过查找差分谱b最大值bk,利用前k个奇异值重构Hankel矩阵,表达式如下:

(5)

2.1.2 差方均值函数拟合时差估计方法

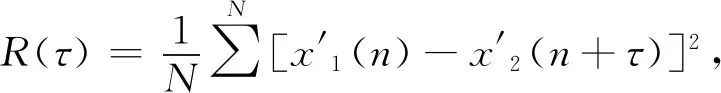
(6)

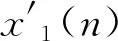
(7)

其中,τm=arg minτ(R(τ)).

2.2 Chan定位方法

Chan定位算法本质上是双曲线定位方法,双曲线定位示意图如图2所示,通过估计干扰源到两接收机时差可以列出双曲线方程,多个双曲线交汇可确定干扰源位置. 完成时差估计后可列双曲线方程如下:

ri,1=cDi=ri-r1,i=2,3,…,N，

(8)

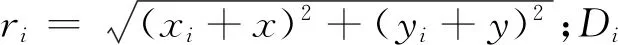
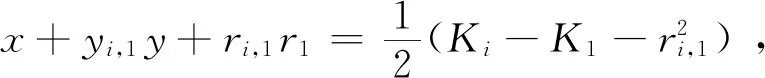
(9)

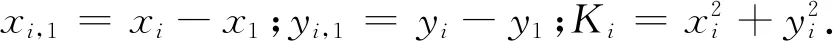
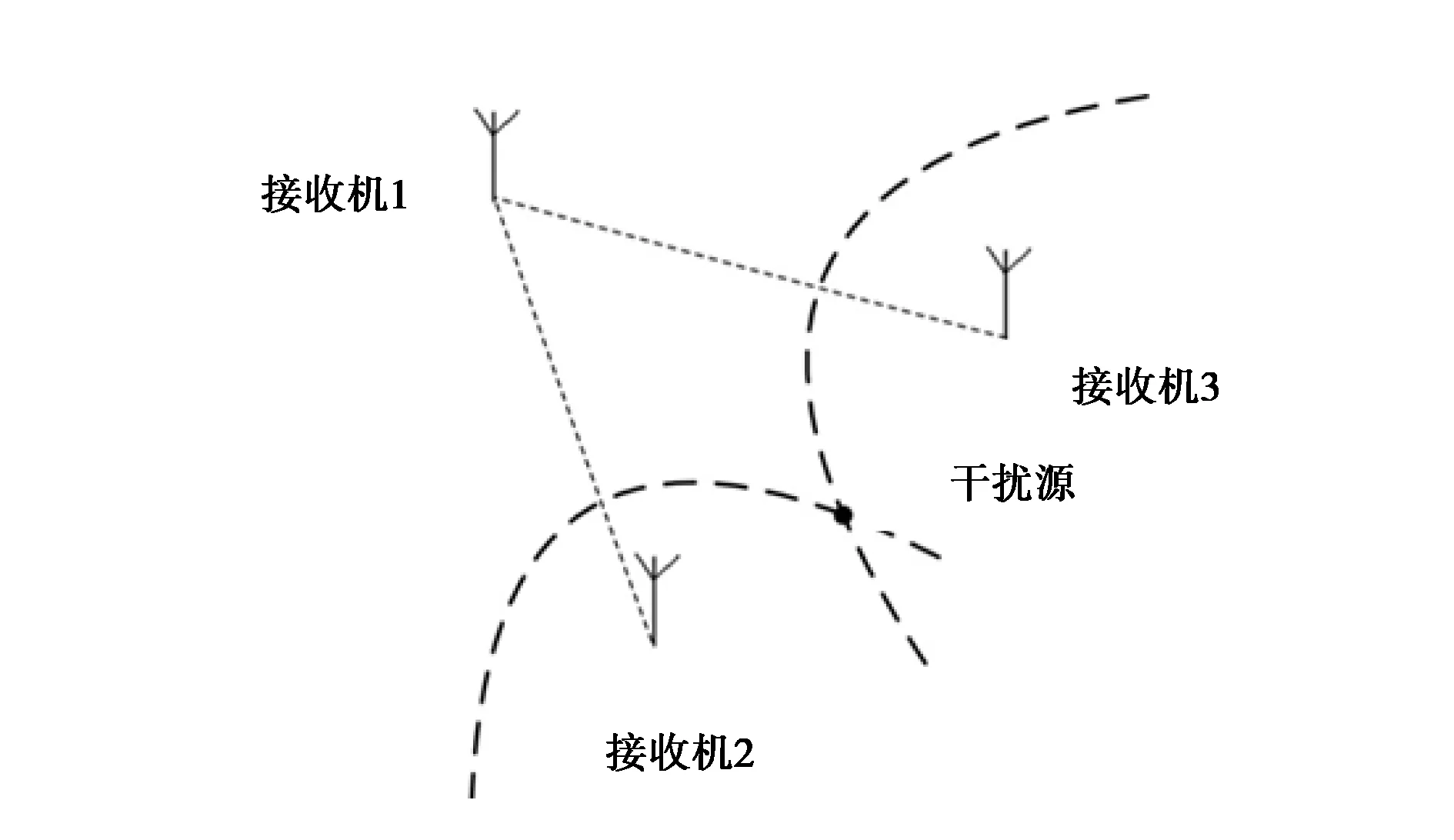
图2 双曲线定位示意图

Chan算法在成高斯分布的时差估计误差下定位效果好,因此较好地适用于本文的应用场景[8]. 方法进行两次加权最小二乘(WLS)以实现双曲线方程的精确求解,通常场景下,双曲线方程冗余,式(9)可写成如下矩阵形式,表达式如下:

Gaza=h,

(10)

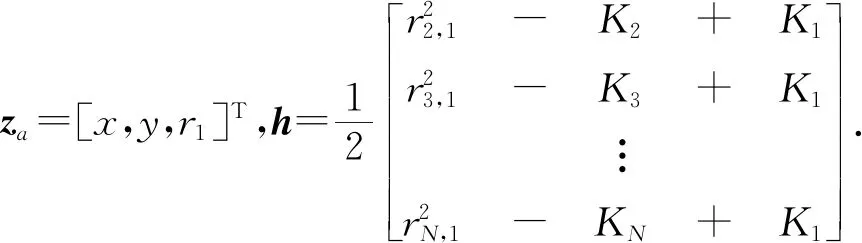
ψ=h-Gaza0，

(11)

式中,za0为无噪声时za值. 依据文献[9-10]可给出式(11)的WLS解,表达式如下:

(12)

利用式(12)得出的解可构造新的方程组进行第二次WLS以改善目标干扰源位置的估计结果,方程组表达式如下:

(13)

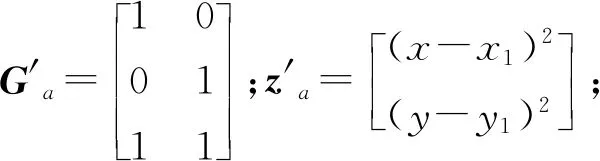
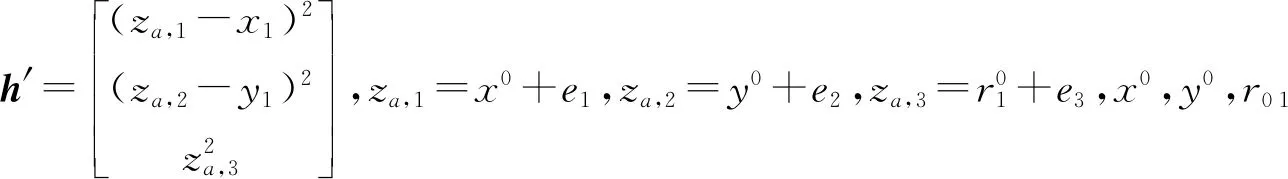
3 仿真分析

仿真模拟真实GNSS弱干扰源网格化定位的应用场景,对比统计本文方法和最为常用的基于GCC的TDOA定位方法的定位精度. 仿真过程中,目标干扰信号s(n)功率设置为-125 dBm,为带宽2.046 MHz的弱干扰信号,添加噪声信号n(n)后目标干扰信号的信噪比(SNR)为-7 dB,目标信号淹没在噪声下,其中n(n)包含功率为-128 dBm的GNSS信号. 信号载频为1575.42 MHz,采样频率为16.368 MHz.

文献[1]建议实际布设网格化监测接收机时,为提升定位效果,需在网络几何中心设置基准接收机. 图3示出仿真接收机布局及干扰源位置,分别仿真典型四接收机和七接收机布局方式下的定位效果,接收机布设在半径1.5 km的圆上,中心布设基准站. 干扰源坐标为(300,500),仿真考虑20 ns的时间同步误差.

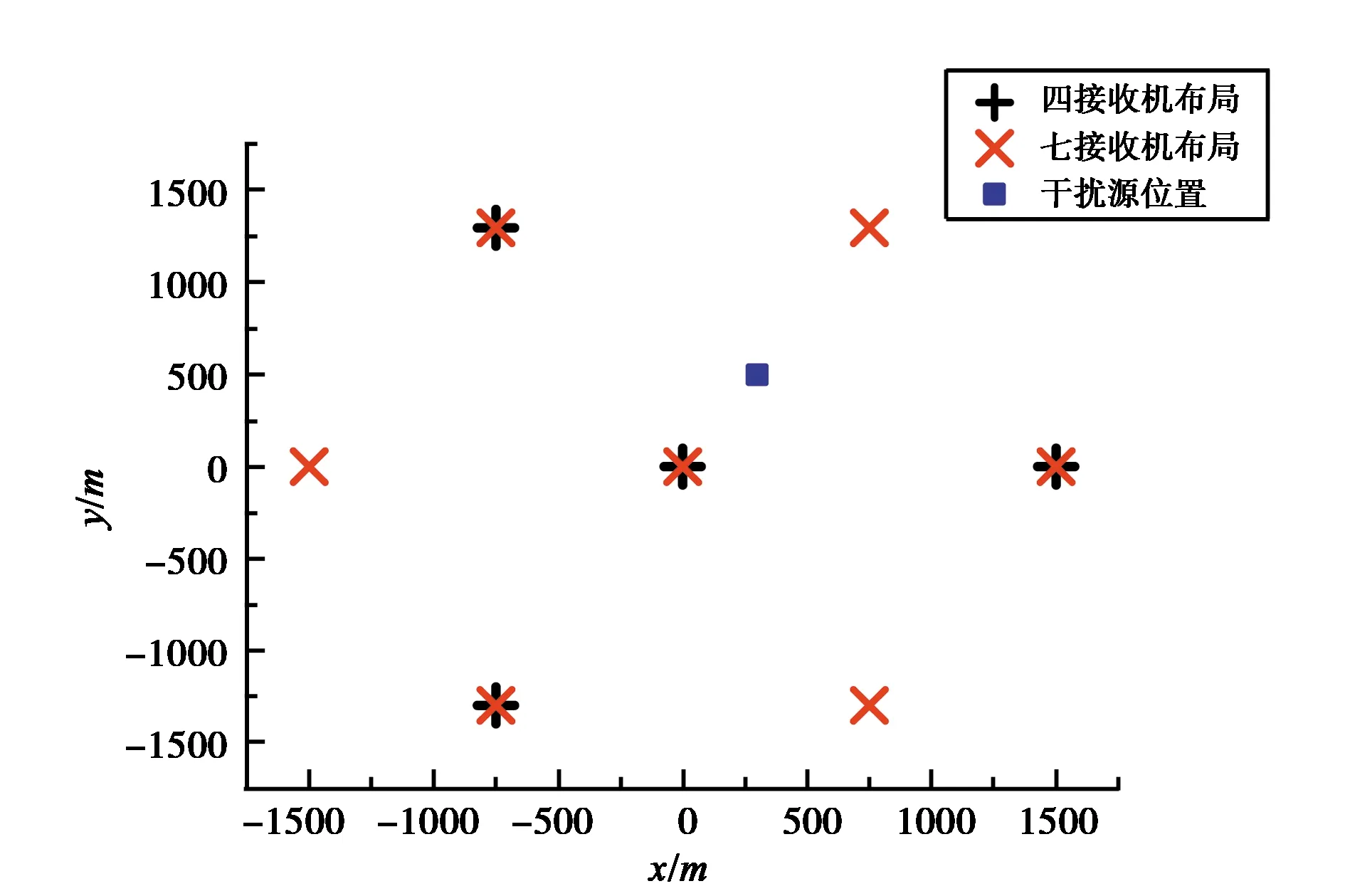
图3 仿真接收机布局及干扰源位置

图4为某次定位处理的奇异值差分谱噪声滤除效果图,其中图4(a)为目标干扰信号采样波形,图4(b)为目标干扰信号混入噪声信号波形,图4(c)为奇异值差分谱噪声滤除后波形.图4表明本文方法可以很好地实现噪声滤除,从而提升弱干扰信号的时差估计效果.

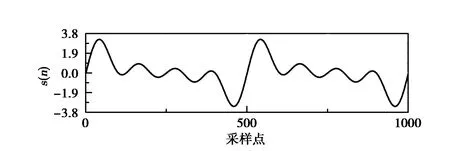
(a)目标干扰信号

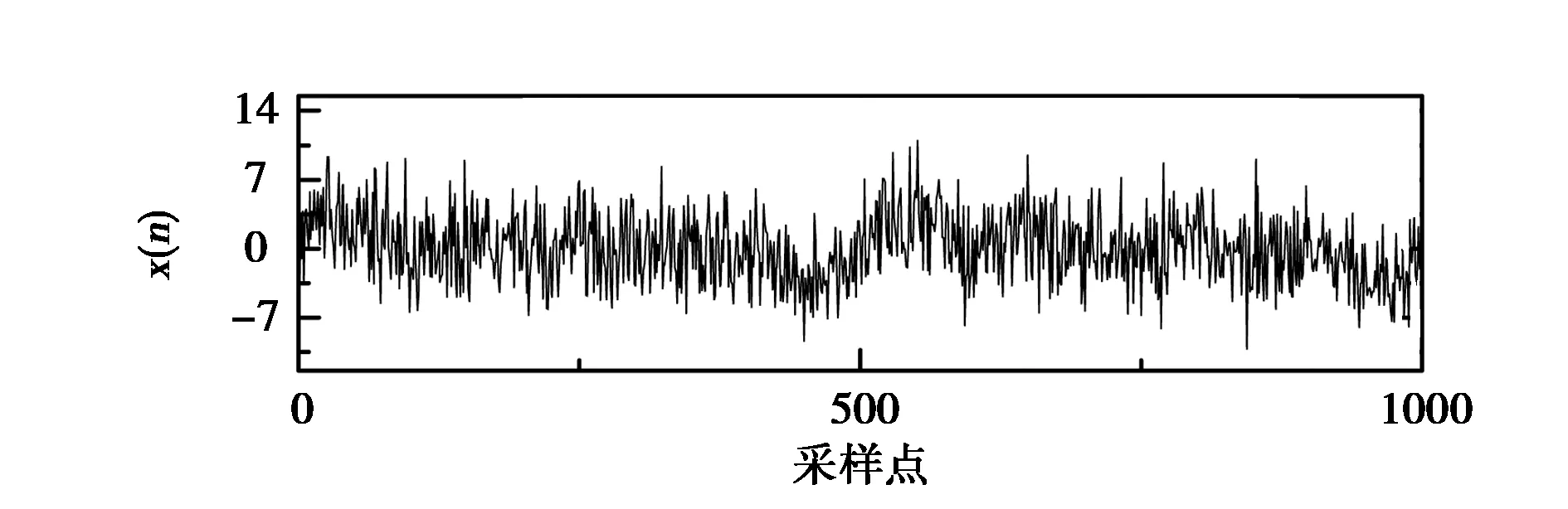
(b)目标干扰信号+噪声信号

(c)噪声滤除结果图4 奇异值差分谱噪声滤除效果

在上文仿真条件下进行200次定位试验,并对定位结果进行统计. 图5～6分别示出四接收机、七接收机本文方法和GCC方法定位效果对比,相对于GCC方法，本文方法定位结果更接近于真实干扰源位置. 对上述场景下不同定位方法的均方根误差(RMSE)进行统计,统计结果如表1所示. 在四接收机情况下,本文方法相比于GCC方法,定位RMSE由70.05 m提升至24.30 m;在七接收机情况下,本文方法相比于GCC方法,定位RMSE由25.92 m提升至7.67 m. 仿真结果表明在弱GNSS干扰定位的场景下,本文方法较好地改善了噪声和导航信号对干扰源定位效果的影响,提升了定位精度.

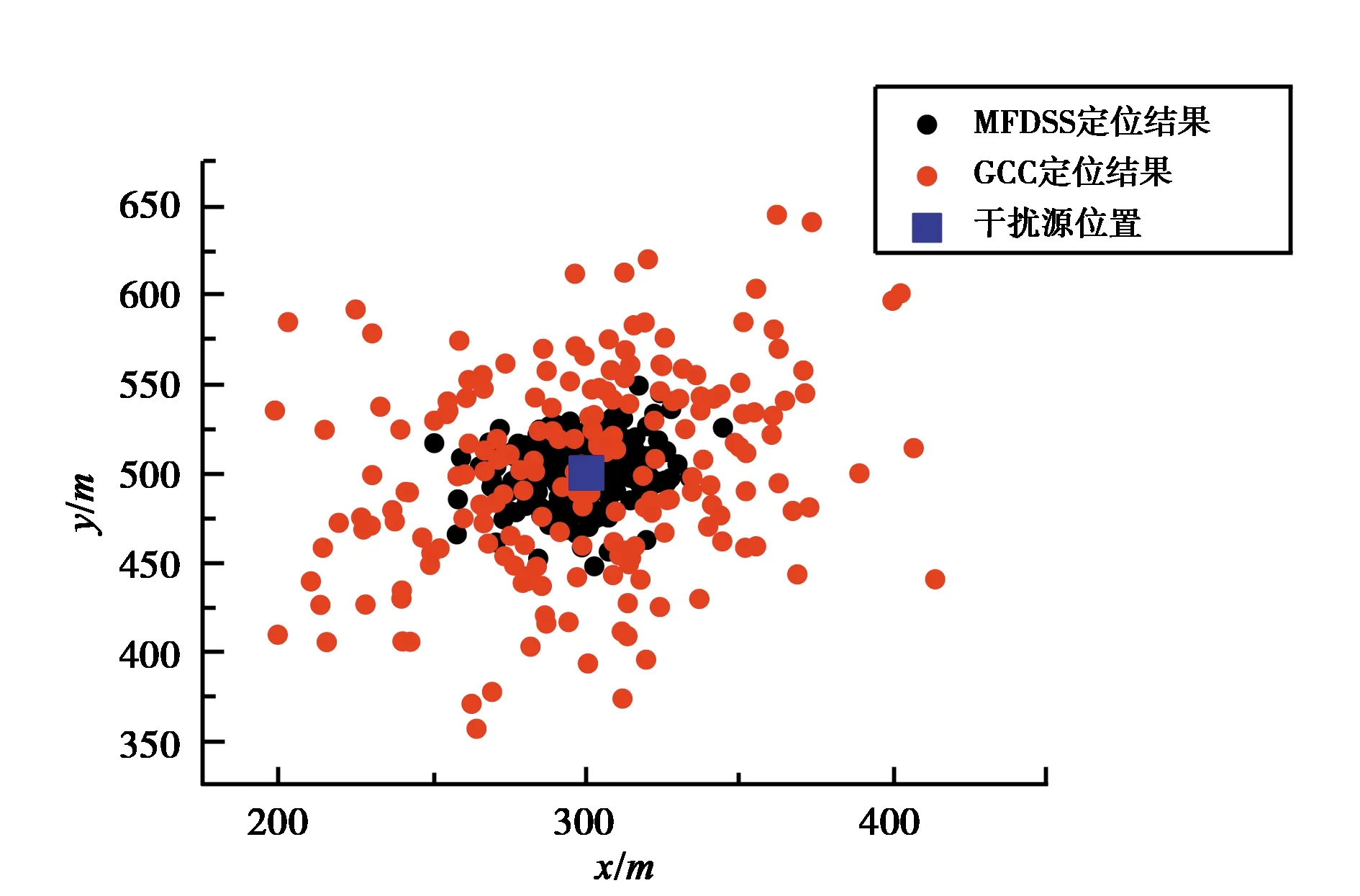
图5 四接收机定位效果

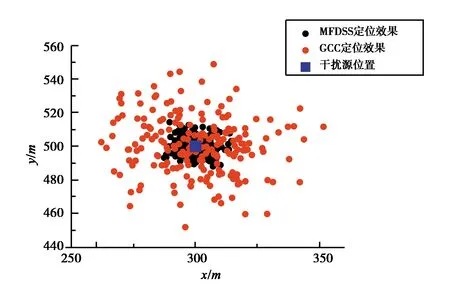
图6 七接收机定位效果

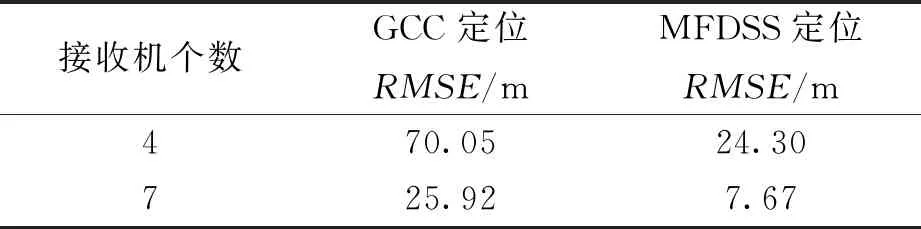
表1 不同场景下的定位RMSE统计

4 结束语

本文介绍了网格化GNSS弱干扰源定位的系统组成,分析了现有方法在该应用场景下尚存的问题,针对这些问题提出了一种基于MFDSS的网格化GNSS弱干扰源定位方法. 文章详细描述了该方法的原理,并针对弱GNSS干扰定位的应用场景和典型接收机布局方式,对比仿真了本文方法和基于GCC的TDOA算法的定位效果. 仿真结果表明该场景下本文方法相对于目前常用的网格化定位方法,定位效果提升明显.