有关“轻杆”的习题研究

卢敏翔

(苏州工业园区星海实验中学，江苏 苏州 215000)

理想化模型的建立过程渗透着研究问题时抓住主要因素、忽略次要因素的哲学思想.建立理想化模型是简化物理研究的重要手段，是一种非常重要的科学研究方法.轻杆是物理学中常见的理想化模型，轻杆在物理上是指不计质量不计形变的刚性杆，具有以下特点.

(1) 合力为0.根据牛顿第二定律，轻杆的合力必然为0.如果轻杆只受两个力，那么这两个力一定是等大反向的，如果受到3个力的作用，那么这3个力一定是共点力(三力汇交原理).

(2) 速度可以突变.质量是惯性大小的唯一量度，质量为0，说明物体运动状态的改变就没有了难度，瞬间就可以获得任意大的速度，这就意味着轻杆的速度是可以突变的.

(3) 不具有任何能量.质量不计，意味着轻杆不具有动能，势能.轻杆速度突变时无需外力做功，也无需消耗任何能量.

在处理轻杆的问题时，要优先抓住轻杆的以上特点来进行分析.下面通过典型的例题，从常见的“动杆”、“定杆”的受力特点出发，由浅入深，全面剖析轻杆在各种习题中的处理技巧.

1 “动杆”、“定杆”的受力特点

例1.如图1(a)所示，水平轻杆BC的B端固定，C端有一定滑轮；如图1(b)所示，水平轻杆BC的B端连接铰链，C端摩擦很大，绳无法移动.当物体静止时，∠θ均为30°，均不计绳子的质量，求两种情况下杆C端对外的弹力大小？

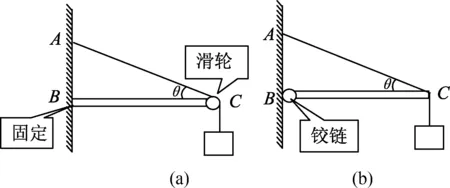
图1

解析：图1(a)中的C端受力分析如图2(a)所示，先求出拉力T1和T2的合力T合=T2=T1=mg，再根据平衡特点得到F与T合等大反向，易知杆C端对外的弹力大小为FN=mg.

图2

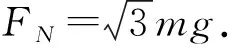
总结：例1是涉及“定杆”和“动杆”受力特点的典型问题.这类问题往往会和轻绳结合起来.图1(a)中的轻杆由于B端固定，因此是一根“定杆”，“定杆”对外提供的力不一定沿杆的方向；C端有光滑定滑轮，因此滑轮两边的绳的是可以自由活动的，这样的结点称为“活结”，“活结”两边绳的力一定是等大的.“定杆”本质上是轻杆一端和外界固定，组合成了一个整体，共同对外施力，方向可以沿任意方向，受力分析时不能单独将“定杆”进行受力分析，需将“定杆”和固连的外界作为一个整体考虑.图1(b)中的杆由于B端可转动，因此是一根“动杆”，要使得“动杆”平衡，外界对杆的力必须沿杆的方向，否则杆就会转动，因此杆对外界的力也必须沿杆的方向；C端结点两边的绳由于摩擦太大不能移动，因此是一个“死结”，“死结”两边的绳的拉力大小不一定相等.“动杆”由于可动，因此静止时，其合力必为0(考虑转动时，其合力矩也必为0).

2 “动杆”和“定杆”的拓展

例2.如图3(a)所示， 已知小球质量为m，小车以加速度a向左做匀加速直线运动，装置中两轻杆固定连接，斜杆与竖直方向均成θ角度，试求轻杆对小球的作用力？

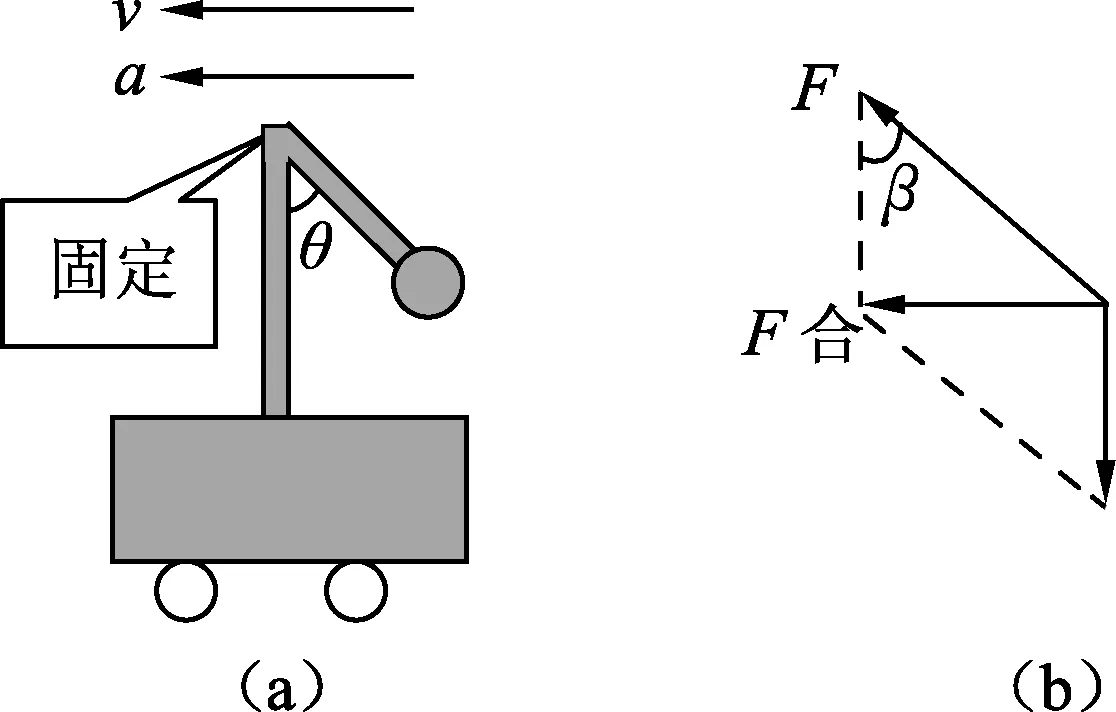
图3

例3.如图4(a)中轻杆BC的B端用铰链接在竖直墙上，另一端C为一轻滑轮.重物G上系一轻绳经过滑轮固定于墙上A点处， 杆恰好平衡.若将绳的A端沿墙缓慢向下移(摩擦均不计)，则绳的拉力和BC杆对绳子的作用力各如何变化？

(a) (b)

解析：轻杆C端为光滑定滑轮，因此绳AC上的拉力和重物的重力G是一直恒等不变的；轻杆B端和铰链相连，是“动杆”，绳AC上的拉力和重物重力的合力F应该要沿杆方向，当绳A端下移时，合力会由F1增加到F2，如图4(b)所示，因此BC杆对绳子的作用力增大.

例3中很多学生在进行受力分析时，误认为杆对小球的弹力F与竖直方向的夹角β和题目中给的角θ是同一个角，得出F=mg/cosθ的错误答案,产生这个错误的原因就是没有认识到整根杆是一根“定杆”，对外提供的弹力F不一定杆沿杆的方向，只有满足a=gtanθ时，才满足β=θ，也即此时杆对小球的弹力才沿杆的方向.例3分析时既要注意到BC杆是“动杆”，结点C是“活结”之外，还要意识到当绳A端下移时，杆BC的形态必然会变化，即BC杆与竖直墙壁的夹角会减小，这是本题的一个难点，也是很多学生在进行受力分析时容易糊涂的地方.

3 轻杆在受力分析中的处理技巧

有一些涉及轻杆模型的题目的情景简单，但是受力分析却很难，解题的关键是如何通过轻杆的特点做出正确的受力分析图.

例4.如图5(a)所示，AC为轻绳，BC为弯曲的硬轻杆，B端用铰链接于竖直墙上， 且AC=BC，当C端挂一质量为m的物体时， 绳AC的拉力为多大？

图5

解析：以C点为研究对象，轻杆对C点的弹力FN方向一定是沿BC连线方向，作出C点受力示意图如图5(b)所示.利用力的矢量三角形和几何三角形相似，可得FT=mg.

例5.轻质横杆OB，O端用铰链固定在墙上，B点用轻绳拉紧，使杆处于水平状态，在B点挂重为G的物体，如图6(a)甲所示，AB和OB的夹角为θ，在把重物的悬点向O端移动的过程中，求墙对杆作用力的最小值.

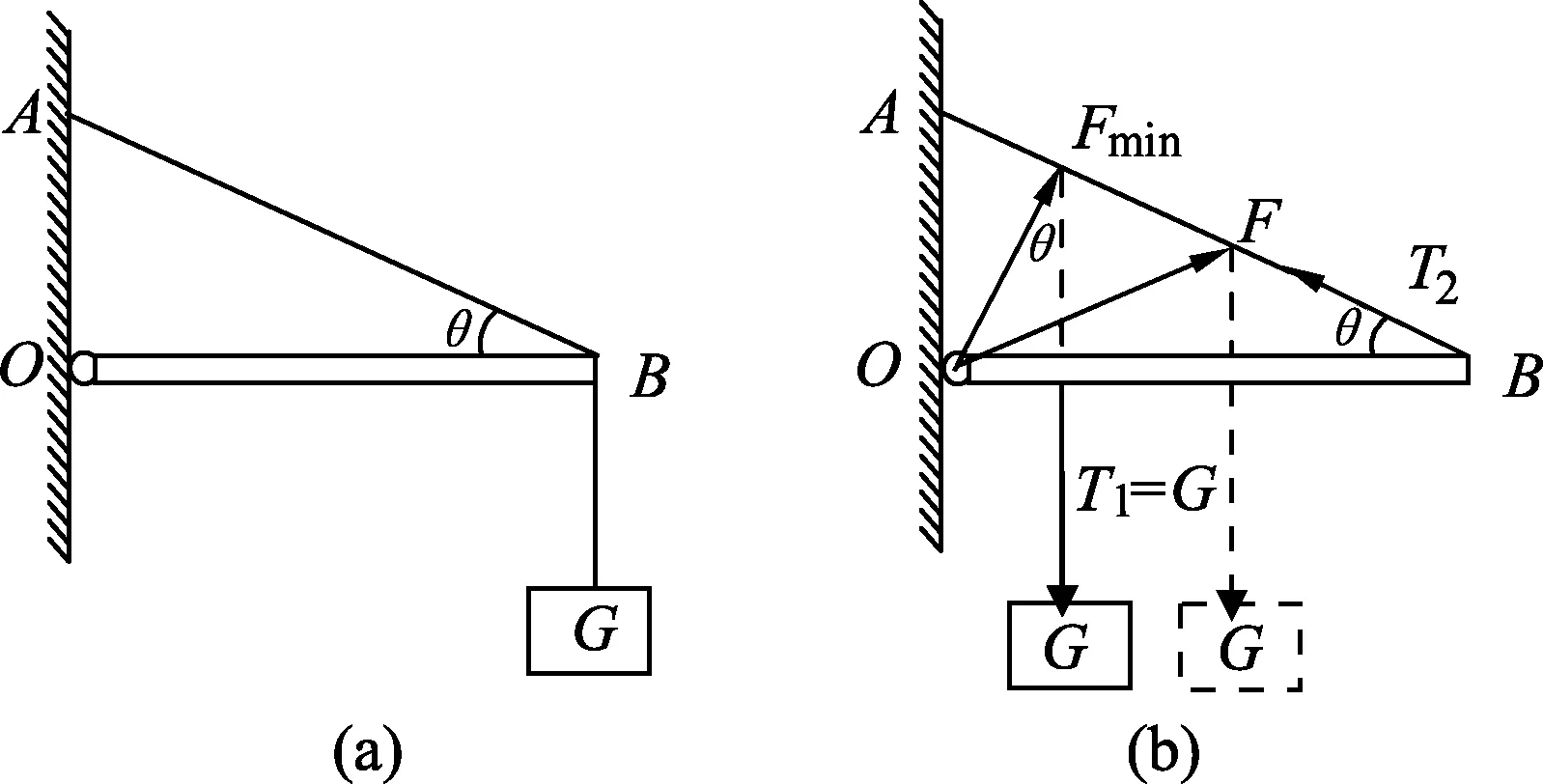
图6

解析：该题中的重物的悬挂点向左移动，考虑整根杆的受力，轻杆受到重物的拉力T1，AB绳的拉力T2，以及墙对杆的力F，如图6(b)所示.由于杆的合力为0，根据3力汇交原理，这3个力必然是共点力，由于T2的方向始终不变，因此F与T2垂直时，F最小，最小值Fmin=Gcosθ.

面对较难的受力分析时，一定要抓住轻杆的合力为0，从而得到正确的受力分析图.例3的关键在于如何确定轻杆对C点的弹力方向，如果仅仅是考虑结点C的受力是无法确定轻杆对C点的弹力方向，此时应该转换研究对象.先对轻杆进行受力分析，轻杆受到两个力的作用， 即两个端点对杆的作用力.由于杆处于静止状态， 这两个力一定是一对平衡力，方向必在B点与C点连线上，从而反过来可以得到杆对C的作用力一定是沿BC方向的.例4的关键是需对整根轻杆进行受力分析，抓住轻杆处于静止状态，巧妙地运用3力汇交，结合动态图像处理力的大小变化特征，避免了繁琐的数学计算.两道题的模型简单，但是受力分析并不简单，而在受力分析中，能否利用好轻杆合力为零的特点，是解题的关键所在.

4 轻杆在综合力学问题中的处理技巧

在综合力学问题中，物理过程复杂多变，如何在复杂多变的过程中理清物理问题的思路，轻杆是关键.

图7

例6.如图7所示，一轻质长木板置于光滑水平地面上，木板上放着质量分别为mA=2 kg和mB=1 kg的A、B两个物块，A、B与木板之间的动摩擦因数都为μ=0.2，水平恒力F作用在A物块上，则下列说法正确的是(重力加速度g=10 m/s2，最大静摩擦力等于滑动摩擦力)

(A) 若F=1 N，则物块、木板都静止不动.

(B) 若F=1.5 N，则A物块所受摩擦力大小为1.5 N.

(C) 若F=6 N，则B物块所受摩擦力大小为2 N.

(D) 若F=8 N，则A物块的加速度大小为3 m/s2.

解析：在A、B均与木板保持相对静止时，A、B所受摩擦力会随拉力增大而增大，以轻木板为研究对象，根据轻木板的合力为0，可知A、B两物体对轻木板的摩擦力始终是等大的，由于A与木板间的最大静摩擦力fA=μmAg=4 N，B与木板间的最大静摩擦力fB=μmBg=2 N，所以一定是B物体所受摩擦力先达到最大静摩擦力.设B物体所受摩擦力刚达到最大静摩擦力时，拉力为F临界，对整个系统使用牛顿第二定律得F临界=(mA+mB)a临界.对物块B使用牛顿第二定律得fB=mBa临界.联立求解得F临界=6 N，a临界=2 m/s2.当F=1 N<6 N时，A、B均与木板保持相对静止，整体在F的作用下向左做匀加速运动，(A)错误.当F=1.5 N<6 N时A、B均与木板保持相对静止，对整个系统使用牛顿第二定律得1.5 N=(mA+mB)a.对物块A使用牛顿第二定律得F-fA=mAa.联立求解得fA=1 N，(B)错误.当F=6 N时B物块所受摩擦力恰好达到最大静摩擦力，(C)正确.当F=8 N>6 N时B物块与轻木板间发生相对滑动，A物体与轻木板间不会发生相对滑动，则A物体的加速度F-f=mAaA，其中f等于B与轻木板间的滑动摩擦力，得到aA=3 m/s2，(D)正确，故选(C)、(D).

例7.某缓冲装置的理想模型如图8所示，劲度系数足够大的轻质弹簧与轻杆相连，轻杆可在固定的槽内移动，与槽间的滑动摩擦力恒为f.轻杆向右移动不超过L时，装置可安全工作.一质量为m的小车若以速度v0撞击弹簧，将导致轻杆向右移动L/4,轻杆与槽间的最大静摩擦力等于滑动摩擦力，且不计小车与地面的摩擦.求：

(1)若弹簧的劲度系数为k，轻杆开始移动时弹簧的压缩量x；

(2)为使装置安全工作，允许该小车撞击的最大速度vm；

(3)讨论在装置安全工作时，该小车弹回速度v′和撞击速度v的关系.

图8

解析： (1) 轻杆开始移动时，弹簧的弹力F=kx，且F=f，解得x=f/k.

(3) 设轻杆恰好移动时，小车撞击速度为v1，则由动能定理可得

例6中的木板是轻质木板，木板的质量是不计的，跟轻杆是一样的.如果以轻木板为研究对象，由牛顿第二定律可得A、B两物体对轻木板的摩擦力大小始终相等.在A、B均与木板保持相对静止，整体在F的作用下向左做匀加速运动过程中，A、B所受摩擦力随着F的增大而增大，在其中一个物体所受摩擦力达到最大静摩擦力后，该物体与木板之间出现相对滑动，另一物体与木板之间摩擦力不再增大、一定不会出现另一物块也相对轻木板滑动的情况.这和“重”木板(考虑木板的质量)是不一样的.这是该题的一个思维难点.突破该难点的方法就是抓住轻板的合力为0.例7中在杆开始移动前，弹簧逐渐被压缩，直至杆开始移动，由于杆的质量不计，杆的合力一定为0，即弹簧弹力与杆收到的滑动摩擦力等大反向，因此弹簧的压缩量不会再变大，之后弹簧和轻杆由于质量不计，能瞬间获得和小车相同的速度并一起开始减速，直至速度为0，速度突变过程中不需要消耗任何能量；当分类讨论小车弹回速度v′和撞击速度v的关系时，当v1≤v≤vm时，由于弹簧被压缩x后就不再变化，储存的弹性势能在杆移动过程中不变，小车弹回时的速度是不变的.对例7分析时只有清楚杆的受力特点和能量特点，才能理清整个过程中的物理思路.

结束语： 虽然实际问题中轻杆模型并不存在，但这种理想化模型的建立与分析恰恰是培养学生科学思维的很好途径.物理中很多不计质量的模型与轻杆模型的分析方法是类似的，如轻绳、轻弹簧等，无论涉及的情景多么复杂，能否抓住这类轻模型的最主要特征会成为解题的关键所在.