渐开线外啮合斜齿轮流量计的流量脉动

杨国来, 陈 晨, 董季澄, 高文涛

(1.兰州理工大学 能源与动力工程学院, 甘肃 兰州 730050; 2. 兰州理工大学 兰石研究院, 甘肃 兰州 730050)

计量是研究测量的一门科学,是所有科学赖以发展的基础.在自然科学的发展中,计量是人们正确认识自然现象、掌握自然规律、验证科学预见不可缺少的手段.在工业生产中,计量同样也有着举足轻重的地位,流量计计量的精确性直接影响着液压系统的稳定性、产品质量以及人身安全.

渐开线外啮合圆柱齿轮流量计结构简单,线性度可以达到0.5%～ 1.0%,测量精度高,适合于测量高黏度介质的流量；由于采用双齿轮对称啮合转动,其测量重复性较高,一般可以达到0.05%.其次,圆柱齿轮流量计可在30～40 MPa这样较高的压力下使用[1-2].正是由于渐开线外啮合圆柱齿轮流量计的上述优点,使其在工业生产、科学实验、航空航天等各个领域得以广泛使用.然而发现,目前广泛使用的渐开线外啮合直齿轮流量计的困油现象在工作过程中产生的周期性流量脉动、噪声、压力冲击等对液压系统的稳定性有较大的干扰.这些缺点限制了其在高精度、高响应、高稳定性的伺服和比例系统中的应用.

渐开线外啮合直齿轮啮合过程中,啮合齿沿着齿宽方向突然啮合,然后又突然分开,两个状态之间没有逐渐过渡的过程.由于斜齿轮存在螺旋角β,其整个啮合过程可分为三个阶段：斜齿轮齿廓逐渐进入啮合状态、完全进入啮合状态、逐渐脱离啮合状态；斜齿轮齿廓的接触线长度沿齿宽方向由零逐渐增加,接着又逐渐缩短,最终至脱离接触；载荷也不是突然加载或突然卸载.因此,斜齿轮流量计工作平稳、流量脉动低、计量精度高.本文针对渐开线外啮合斜齿轮流量计流量脉动低于渐开线外啮合直齿轮流量计流量脉动的根本原因展开研究,并对减小斜齿轮流量计流量脉动的关键参数作进一步研究[3].

1 斜齿轮流量计关键参数的推导

斜齿轮流量计的瞬时流量可依据齿轮的啮合原理以及能量守恒定律进行推导.假设不考虑其他任何损失,流量计主动齿轮每转过一个微小角度记为dθ1,两个互相啮合的斜齿轮转子所消耗的机械功率dW等于流量计所排出的介质体积dV与其进出口压差Δp的乘积(流量计的工况属于马达工况),由能量守恒定律得出[4]：

T1dθ1+T2dθ2=dW=ΔpdV

(1)

式中：T1、T2分别为主动、被动齿轮的输出转矩；dθ1、dθ2分别为主动、被动齿轮的旋转角度.

图1为斜齿轮流量计模型简图.图中a1和a2分别为斜齿轮啮合点c到主动、被动齿轮旋转中心的距离；Re1和Re2分别为主动、被动齿轮的齿顶圆半径.作用在流量计主动齿轮上的液压力会对其旋转中心产生转矩,大小为

(2)

式中：dx为斜齿轮在齿宽方向的微小长度.

同理,作用在被动齿轮上液压力产生的转矩：

(3)

将式(2)和式(3)代入式(1)中可得

(4)

在齿轮传动的参数计算中有如下关系：

式中：R1和R2分别为主动、被动齿轮的节圆半径.

对式(4)进行简化,乘以角速度ω,得出其在齿宽方向的宽度为dx的瞬时体积流量的数学表达式：

(7)

式中：qV,i为宽度为dx的瞬时体积流量.

图2为基准面o-o上啮合点c和中心点h的几何关系模型简图,图3为图2中局部放大区域Ⅰ的各点几何关系图.

令f为齿轮啮合点c与两齿轮中心点h之间的距离,α为f与水平方向的夹角.由图3所示的几何关系以及三角形三边的求解公式得出：

(8)

由于斜齿轮存在螺旋角β,致使其啮合点c随着齿轮旋转角度的不断变化而沿着啮合线移动,因此齿轮不同基准面上的啮合点c与啮合齿轮中心点h的距离f是不同的,如图4所示.图4中c0、h0分别为基准面o-o上的啮合点和中心点,cx、hx分别为基准面x-x上的啮合点和中心点,c0、cx两点间的直线即为两齿轮的啮合线.

结合图3和图4,根据三角形的几何计算关系,可用斜齿轮转角得出f的表达式：

(9)

式中：Rb为基圆半径；θ0为选定基准面上与斜齿轮啮合点相对应的斜齿轮转角；θx为与选定基准面距离为x的同一对啮合齿的啮合点所对应的斜齿轮转角.

将式(8)和式(9)代入式(7),化简可得

(10)

依据上式,斜齿轮流量计瞬时流量随斜齿轮的转动角度θ0呈抛物线变化规律.

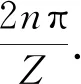
(11)

式中：qV为整个齿宽方向的体积流量.

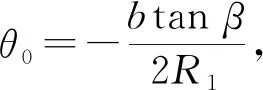
(12)

(13)

(14)

(15)

斜齿轮流量计的流量脉动以平均流量脉动值为基准在其上下作周期性变化,最大变化量ΔqV=qV,max-qV,min.综上,可得出：

(16)

当螺旋角β=0时,直齿轮流量计流量脉动最大变化量的数学表达式为

(17)

由以上推导可以看出,斜齿轮流量计的流量脉动与斜齿轮转动的角速度ω呈正相关关系,与齿数Z、齿宽b、螺旋角β呈负相关关系.从减小斜齿轮流量计的流量脉动,提高其计量精度和增大齿容量的同时又缩小流量计体积的角度考虑,渐开线外啮合斜齿轮流量计的最大设计转速一般为3 000～6 000 r/min,斜齿轮的齿数一般为13～14个.因此,对斜齿轮的临界螺旋角β、临界齿宽b的研究就显得尤为重要.

2 临界螺旋角、齿宽的推导[7]

图6为斜齿轮啮合面的展开图.图中为从动斜齿轮,旋向为右旋.ABCD表示斜齿轮逐渐啮入的第n个啮合齿,A1B1C1D1～A3B3C3D3表示同一个啮合齿,不同转角的前后端面的啮合状态.随着啮合轮齿的转动,啮合齿从BH处逐渐进入啮合状态,在点A处前端面的齿顶尖角开始啮合,当啮合齿转动到点A1处时,后端面的齿顶尖角进入啮合状态,此时啮合齿沿着整个齿宽方向进入完全啮合状态；当啮合齿转动到点A2处,前端面齿廓开始逐渐分离；当啮合齿转动到点A3处,后端面齿廓逐渐脱离啮合状态.当两轮齿的齿廓接触线处于ABH区域时,该对啮合齿处于非完全啮合状态.虽然此时斜齿轮可以连续传动,但不能将斜齿轮流量计的高、低压腔有效的隔开,所以起不到密封的作用,从而严重影响了斜齿轮流量计的计量精度；当该对啮合齿的齿廓接触线处于AA1B1区域时,两轮齿此时处于完全啮合状态,不但能保证传动的连续性,而且还能将斜齿轮流量计的高、低压腔进行有效的隔开；当该对啮合齿的齿廓接触线处于A2A3B3区域时,两轮齿又一次处于不完全啮合状态.此时,不能够对斜齿轮流量计的高、低压腔进行有效的隔开.由以上分析可知,为了保证斜齿轮传动的连续性和渐开线外啮合斜齿轮流量计的计量精度就必须保证前一对啮合齿的齿廓接触线完全脱离全齿宽啮合区域的同时,后一对啮合齿的齿廓接触线紧接着进入AA1B1啮合区域,而要使该对啮合齿轮在啮合过程中一直有齿廓接触线位于全齿宽啮合区域内就必须满足[8]：

LAD1≥Pbt

(18)

式中：LAD1为图6中A、D1两点间的距离；Pbt为斜齿轮的断面基节.

斜齿轮的重合度为

(19)

结合以上两式有：

(20)

式中：b为齿宽；βb为基圆上的螺旋角.

化简后得

(21)

式中：β为斜齿轮分度圆上的螺旋角；mn为斜齿轮法面模数.

由机械原理斜齿轮重合度的定义,总重合度：

ε=εα+εβ

(22)

式中：εα为斜齿轮的端面重合度；εβ为斜齿轮的轴向重合度.

(23)

(24)

式中：Z1、Z2分别为主动、被动齿轮的齿数；αt1、αt2分别为主动、被动齿轮齿顶圆压力角；α′为齿顶圆端面啮合角.

αt1=αt2、Z1=Z2,对式(22)进行整理：

(25)

由式(25)分析可知,斜齿轮流量计的总重合度ε由两部分组成.一部分是全齿宽啮合区域,称之为ε1；另一部分是不完全齿宽啮合区域,称之为ε2.其中：

(26)

故有：

(27)

(28)

即

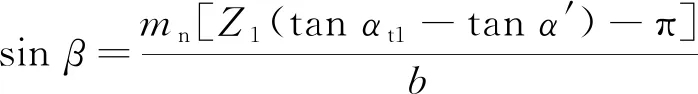
(29)

综上,渐开线外啮合斜齿轮流量计不产生困油现象的临界螺旋角为

(30)

临界齿宽为

(31)

3 结论

1) 渐开线外啮合斜齿轮流量计流量脉动与斜齿轮的角速度、模数、螺旋角以及齿宽有关.

2) 渐开线外啮合斜齿轮流量计的流量脉动低于相同齿容量条件下的直齿轮流量计,且随着螺旋角的增大其流量脉动会减小.

3) 在满足工况要求的前提下,合理地选择渐开线斜齿轮流量计的角速度、模数、螺旋角以及齿宽可大大减小其流量脉动,提高其计量精度.