毫米波MIMO系统中部分连接型混合预编码设计
郑兴林,王 月,刘 伟
重庆邮电大学 通信与信息工程学院,重庆 400065
1 引言
毫米波大规模多输入多输出(Multiple-Input Multiple-Output,MIMO)系统,由于其高带宽和高频谱效率而成为下一代通信系统的关键技术[1-4]。例如,在30 GHz 的载波频率下,波长为10 mm,这使得大量天线可以封装在微小区域中。大规模天线阵列能够带来较高的波束赋形增益,以补偿毫米波信号的高路径损耗[4]。然而,在传统的MIMO 系统中,传输预编码通常只考虑数字域,并且需连接与天线数量相同数目的射频(Radio Frequency,RF)链路[5-8]。毫米波系统结合大量天线阵元,抵消路径和穿透损耗,由于硬件成本和功耗很高,传统全数字预编码在毫米波通信系统中是不可行的。为了解决这一问题,文献[9]提出了混合预编码的概念,用两阶段的预编码器代替传统纯数字预编码器。首先用小型数字预编器对信号进行处理,然后用大型模拟预编码器得到高波束形成增益。
目前混合预编码方案有全连接(Fully-Connected,FC)和部分连接(Partially Connected,PC)结构[10],发送端系统模型如图1 所示。在全连接结构中,每条RF 链通过大量移相器与所有天线连接,以最大化实现可达到的传输增益,然而将会导致高能耗[11]。相比之下,部分连接结构需要较少数量的移相器,虽然性能有所损失,但能带来更高的能源效率[12]。对于全连接型混合预编码的研究,文献[13]提出了基于流形优化的交替算法(MO-AltMin Algorithm,MO-Alt)来接近全数字预编码器的性能,然而,模拟预编码器的更新涉及到线性搜索算法,嵌套循环将减慢整个求解过程,复杂度很高。文献[14]采用DFT码本构成模拟预编码矩阵,大大降低了算法复杂度,但由于模拟预编码是从DFT 码本集中选取,没有很好的匹配信道,性能增益小。对于部分连接型混合预编码,由于其能耗更低,是近年来研究热点。文献[13]利用半定松弛(Semidefinite Relaxation,SDR)思想,提出一种交替最小化算法,通过凸优化工具箱(Convex optimization toolbox,CVX)求解数字预编码器,每一次迭代需要借助标准凸优化算法来求解半定规划(Semidefinite Programming,SDP)问题,导致复杂度较高。文献[15]中利用注水算法设计数字预编码,将模拟预编码设计等效为单天线功率约束下单流最优发射机波束形成问题,复杂度很高。

图1 发送端混合预编码系统模型
基于上述分析,考虑工程实际应用,本文研究部分连接型混合预编码。证明了信道右奇异值向量的相位角来初始化模拟预编码器的可行性。为了获取更优的性能和更高的能源效率,设计了一种基于SVD 的交替迭代(Alternating Iterative SVD,Alt-ISVD)混合预编码算法。仿真结果表明,所提算法随着信噪比增加,性能更加优于传统部分连接型算法,且复杂度与文献[15]提出的算法相比明显降低,与传统正交匹配追踪(Orthogonal Matching Pursuit,OMP)算法[8]相比拥有更高的能源效率。
2 系统模型与信道模型
2.1 系统模型
考虑下行链路毫米波单用户系统,基站(Base Stations,BS)侧配备Nt根发射天线,发射端射频链路数为NtRF,系统模型如图1(b)所示。每条RF 链路仅与一个独立的子阵列相连,且每个独立子阵列均包含M根天线,即从图1 可以看出,当基站配有Nt根天线,全连接型中模拟域需个移相器与所有天线相连,而部分连接型中模拟域只需Nt个移相器与部分天线相连,因此采用部分连接结构,硬件成本和功耗更低,更贴切实际应用。发送端有Ns条数据流发送,数据流s∈ℂNs×1首先在数字域经数字基带预编码器进行预处理,然后在模拟域经过模拟预编码器调相到各天线阵元,形成波束赋形增益,经过两阶段预编码器,最终的发送信号为:

式中,发送信号s应满足,模拟预编码器和数字预编码器应满足总的功率限制Ns。其中,E[⋅]表示求期望,I为单位矩阵表示Frobenius范数。接收端经过解码处理后信号为:

式中,ρ为接收功率,WBB和WRF分别表示为接收端数字合并器和模拟合并器。FRF和WRF应满足单模限制,即维毫米波几何信道矩阵。分布的加性高斯噪声。其中,(⋅)H表示取共轭转置,Nr为移动台(Mobile Station,MS)配有的天线数目。
2.2 信道模型
考虑到毫米波信道的有限散射特性,本文采用扩展的Saleh-Valenzuela簇信道模型[9],窄带毫米波信道矩阵H表示为:
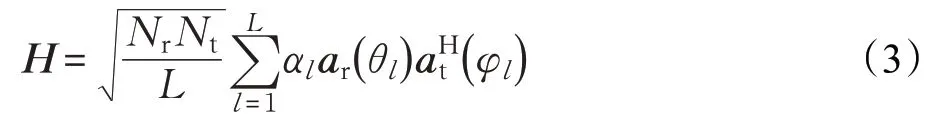
式中,L为系统传播路径数,且每条簇能够产生一条传播路径。αl为服从CN(0,)分布的第l条路径的复增益,矢量ar(θl)和at(φl)分别定义为接收和发送阵列矢量,其中,θl∈[0,2 π]和φl∈[0,2 π]是第l条径的到达和离开方位角。当收发端天线阵列为均匀线阵(Uniform Linear Array,ULA)时,发送和接收天线阵列归一化响应矢量表示如下:
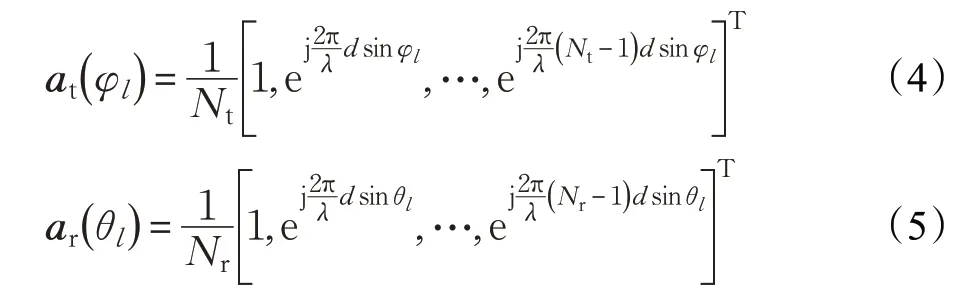
式中,λ为载波波长,d为天线间距。
2.3 问题描述
本文设计混合预编码的目标是减小算法复杂度,提高系统频谱效率。系统频谱效率表示为:


发送端预编码器和接收端合并器优化问题的数学公式相似,只是预编码矩阵设计需要考虑功率约束,因此本文主要研究发送端预编码器的设计。
首先对H进行奇异值分解H=UΣVH,其中,U和V分别为H对应的左奇异值矩阵和右奇异值矩阵,Σ为特征矩阵。将H=UΣVH代入式(7)得:

对Σ,V进行分块表示:

式中,Σ1为Ns×Ns维对角阵,V1的维度为Nt×Ns,最优无约束预编码器Fopt=V1,将式(9)代入式(8)中,则式(8)中部分项可以表示为:
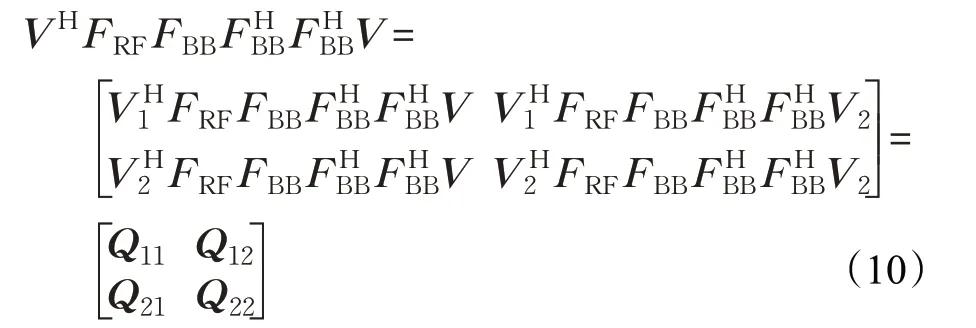
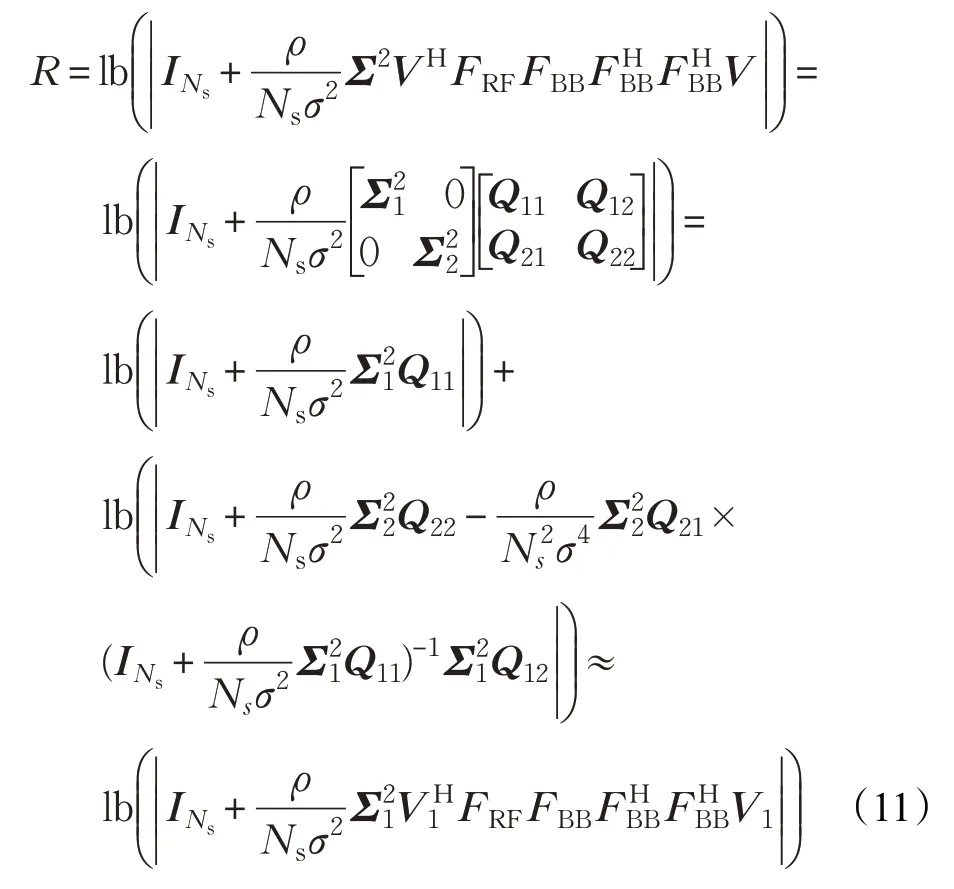

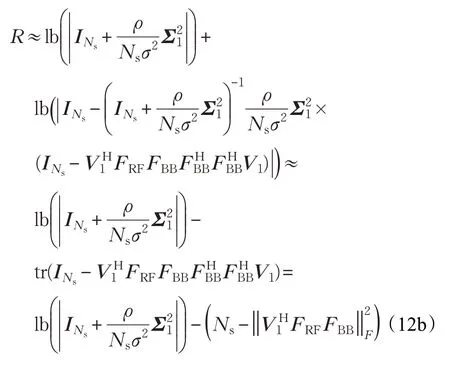
式(12a)表示应用:lb(|INs-X|)≈lb(1-tr(X))=-tr(X),其中,tr(⋅)表示矩阵或矢量的迹。式(12b)表示采用高有效信噪比近似,即由式(12)得,获取最大化R等价于最大化,即FRFFBB越接近于Fopt=V1时,R最大。由以上分析可知,最大化频谱效率等效于混合预编码矩阵与最优预编码矩阵间欧式距离最小的,即:
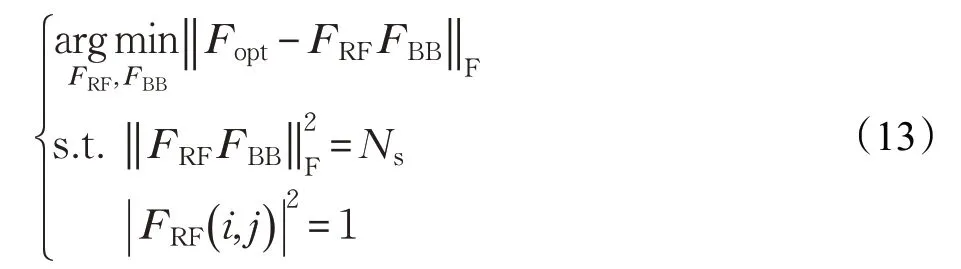

式中,FRF的维度为中每一块向量为fi=j=1,2,…,Nt为第j个相移器的相位。
3 混合预编码设计
考虑单用户传输场景,本文采用部分连接结构,证明了信道矩阵H的有序右奇异值向量角度可以作为初始化模拟预编码矩阵,不需要发射机处的天线阵列响应矢量。
3.1 初始化模拟预编码器设计
根据文献[9]和[13]中分析,混合预编码优化问题可以重写为:
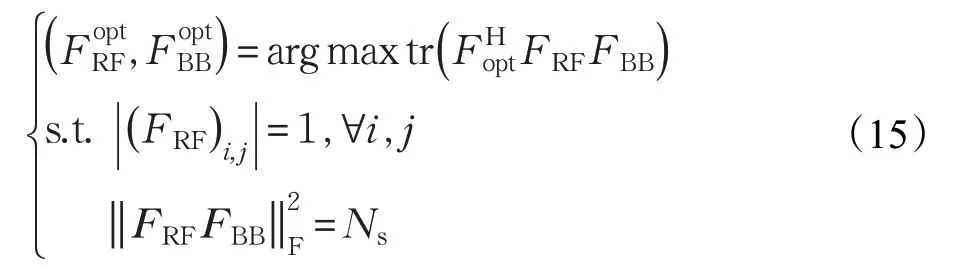


由式(17)可得:

将式(11)代入式(10)中得到:
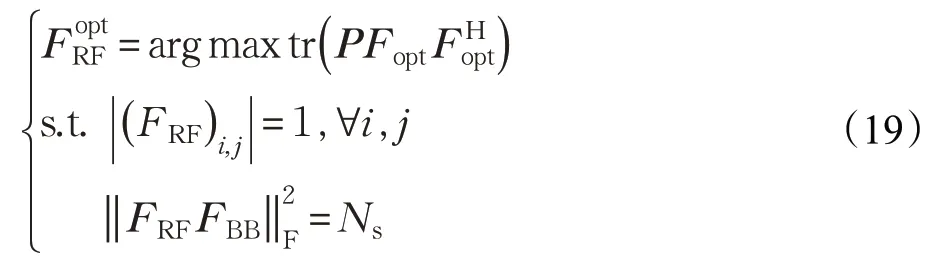
命题1给定矢量,集合F={f∈ ℂN×1:|f(n)|=1,∀n} ,对任意f∈F,有:
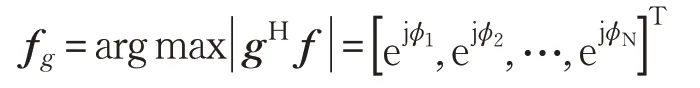
证明设,则有:

根据命题1可知,要使SRF和Sopt内积最大,则FRF和Fopt构成的子空间相同,已知Fopt为信道矩阵右奇异值矩阵,对应相位角度构成其子空间,由于单模限制,则FRF可取信道右奇异值矩阵元素对应的相位角度构成。
通过以上分析可知,可用信道矩阵右奇异值矩阵元素的相位角度初始化模拟预编码器。具体初始化过程即:

式中,U为Nr×Nr维酉矩阵,V为Nt×Nt维酉矩阵,Σ是对角矩阵,且对角元素按降序排列。设φm,n为V的第m行和第n列元素的相位角度,取V中元素的相位角度作为集合F,即:


也即取F 集的前NRF列矢量。应用到式(14)中,进行块对角化,则最终得到的初始模拟预编码矩阵为:

式中,vi((i-1)M+1:iM)表示取vi中第(i-1)M+1 至iM个元素。
3.2 应用交替迭代结构设计
获取初始化模拟预编码器FRF后,应用交替最小化结构,固定FRF,根据最小化Fopt和FRFFBB的欧氏距离,优化FBB,取:


4.1 实验仿真分析
本文仿真基于部分连接结构下毫米波MIMO系统,其中毫米波信道路径数L=10 ,ULA 的天线间距为d=λ/2,假设到达和离开方位角在[0,2 π]上均匀分布。本节给出了在低信噪比和高信噪比下以及不同射频链路下Alt-ISVD 算法的频谱效率的仿真曲线,并仿真了不同射频链路下Alt-ISVD 算法的能效。实验仿真中,发射天线数目为Nt=128,接收天线数目为Nr=16 或Nr=32。
在收发端天线配置为Nt×Nr=128×16 且发送端射频链4,数据流数为Ns=4,低信噪比下不同算法的频谱效率随信噪比变化曲线如图2所示,可以看出,本文Alt-ISVD算法性能优于文献[13]提出的Alt-SDR算法和文献[15]提出的算法1,且随着信噪比增大,差异越明显。随着信噪比增大,本文所提算法性能越来越接近文献[15]提出的算法2,但复杂度低于文献[15]提出的算法1和算法2。

图2 低信噪比下,Nt×Nr=128×16 且=Ns=4时的系统性能
图3 所示为Nt×Nr=128×16 且s=4 时,高信噪比下,不同算法的频谱效率随信噪比增加的曲线,由图可知,在高信噪比下,本文所提Alt-ISVD 算法明显优于文献[13]Alt-SDR算法和文献[15]提出的算法1。当信噪比约大于5 dB 时,Alt-ISVD 算法的频谱效率高出文献[15]提出的算法2,并且随着信噪比增加,性能越优于文献[15]提出的算法2。
图4 所示为SNR=0 ,Nt×Nr=128×32 且Ns=2时,不同射频链路数目下,本文Alt-ISVD 算法、全连接OMP 算法、全数字预编码器和文献[13]Alt-SDR 算法频谱效率曲线。由图可知,本文Alt-ISVD 算法与全连接OMP算法相比,性能略低,这是由于使用较少的相移器带来的性能损失,但本文Alt-ISVD算法性能高于文献[13]Alt-SDR算法。
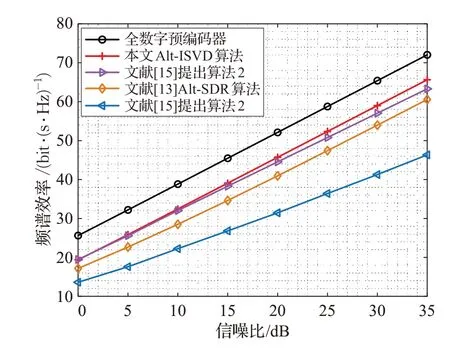
图3 高信噪比下,Nt×Nr=128×16 且=Ns=4时的系统性能

图4 SNR=0,Nt×Nr=128×32 且 N s=2时,不同射频链数的系统性能
本文还仿真了不同数目下,Alt-ISVD 算法、全连接OMP算法、文献[13]Alt-SDR算法的能源效率,仿真参数设置为:Pco=10 W,PRF=100 mW,PPA=100 mW 和PPS=10 mW[13]。根据文献[13],能效计算公式为:

式中,Pco为发送端公共功率,PRF,PPA和PPS分别为每条RF链,功率放大器和移相器的功率。其中,全连接移相器个数为,部分连接移相器个数为NPS=Nt。
图5所示为SNR=0,Nt×Nr=128×32 且Ns=2 时,不同射频链路数目下,本文Alt-ISVD算法、全连接OMP算法、文献[13]Alt-SDR算法能源效率曲线。由图可知,本文所提Alt-ISVD算法的能效高于全连接OMP算法和文献[13]Alt-SDR 算法,且随着RF 链数增加,本文Alt-ISVD算法与OMP算法的能源效率比值越高,这是因为随着RF 链数增加,全连接OMP 算法的移相器增加,大大增加了功耗。

图5 SNR=0,Nt×Nr=128×32 且 N s=2时,不同射频链数的能源效率
4.2 算法复杂度分析
文献[15]的算法和提出的Alt-ISVD 算法复杂度如表1 所示。本文所提算法利用信道右奇异值矩阵的前列来初始化模拟预编码器,根据截短SVD(Truncated SVD,TSVD)[16],复杂度为,获取最优数字预编码器复杂度为,每次迭代更新数字预编码器复杂度为每次迭代更新模拟预编码器复杂度为文献[15]算法1 中,初始化复杂度为,每次迭代复杂度为,其中rH=rank(H),利用注水算法求数字预编码器复杂度为在文献[15]算法2 中,每次迭代获取模拟预编码器的复杂度为,数字预编码器通过注水得到,算法复杂度为在实际传输系统中,Ns≤NRF≪M <Nr<Nt,可以得出,本文所提Alt-ISVD算法复杂度比文献[15]更低。

表1 文献[15]算法和Alt-ISVD复杂度
5 结束语
考虑实际工程应用,全连接型混合预编码能耗太高。文章研究了毫米波MIMO 系统中部分连接型混合预编码,证明了初始化模拟预编码器可由信道右奇异值向量的相位角度导出,可以避免采用搜索近似最佳模拟预编码矩阵的复杂优化过程且不需要知道发射天线阵列响应矢量,降低了复杂度,最后交替应用最小化结构提升性能。仿真结果表明,随着信噪比的增高,本文所提算法性能高于文献[15]提出的算法,且复杂度更低。与传统OMP 算法相比,本文所提算法拥有更高的能源效率,降低了硬件功耗,更贴切实际应用。

