非奇异H-矩阵的含参量的迭代判据

张俊丽

(内蒙古民族大学 数理学院, 内蒙古 通辽 028043)

非奇异H-矩阵在控制论、电力系统理论、经济数学以及弹性力学等许多领域中有着广泛的应用.但是,非奇异H-矩阵的数值判定却很困难,国内外很多学者对其进行了深入的研究[1-21].本文在文献[4]的基础上,通过对指标集作重新划分,给出了非奇异H-矩阵的含参量的新判据,数值算例表明该判据是有效的.

首先引入符号和定义：

用Cn×n表示n×n阶复矩阵的集合.α∈(0,1],N={1,2,…,n},

Ostrowski[1]1937年给出了非奇异H-矩阵的定义. 矩阵A=(aij)∈Cn×n是非奇异H-矩阵的直观定义是其比较矩阵M(A)为非奇异M-矩阵,其中M(A):=(bij)定义如下：

下面给出广义对角占优矩阵的定义,它与非奇异H-矩阵的定义等价[8].

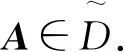
定义2[8]设A=(aij)∈Cn×n,如果∃α∈(0,1],使得对∀i∈N,有

|aii|≥(>)(Λi(A))α(Ci(A))1-α

定义3设A=(aij)∈Cn×n,若A∈D0(α)是不可约的,且至少有一个不等式是严格的,称A为不可约α-链对角占优矩阵；若A∈D0(α),并对于满足等式成立的下标i都存在非零元素链aii1,ai1i2, …,aikj,满足|ajj|>(Λj(A))α(Cj(A))1-α,称A为具有非零元素链α-链对角占优阵.

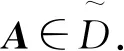
1)A∈D(α);

2)A为不可约α-链对角占优矩阵;

3)A为具有非零元素链α-链对角占优矩阵.

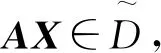
首先给出如下符号：

记

N={1,2,…,n}

N1={i∈N:0<|aii|≤(Λi(A))α(Ci(A))1-α}

N2={i∈N:|aii|>(Λi(A))α(Ci(A))1-α}

∀i∈N2,p=0,1,2,…

r′p(A)=

p=0,1,2,…

1 主要结果

定理1设A=(aij)∈Cn×n,α∈(0,1],若存在非负整数p, 使得A满足如下条件之一:

(1)

(2)

令

(3)

(4)

由式(3)得

(5)

构造正对角阵X=diag(x1,x2,…,xn),并记B=AX=(bij), 其中,

xi=1,∀i∈N1;xi=δi(A)+ε,∀i∈N2

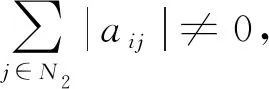
于是

由式(2)

② ∀i∈N2,δi(A)<1, 故

|bii|=(δi(A)+ε)|aii|=δi(A)|aii|+ε|aii|>

[Λi(A)]α[Ci(A)]1-α+ε[Λi(A)]α[Ci(A)]1-α=

[Λi(A)]α(1+ε)α[(1+ε)Ci(A)]1-α>

[Λi(A)]α(1+ε)α[(δi(A)+ε)Ci(A)]1-α>

[Λi(B)]α[Ci(B)]1-α

(6)

故存在ε,满足：

由r′p的定义知:

于是

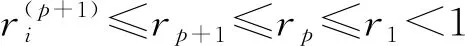
因此,对∀i∈N, 有

定理1中的迭代判据亦可作如下形式的推广：

(7)

证明由A不可约,故∀i∈N′⊂N,∀j∈N-N′,由|aij|不全为零.

且至少有一严格不等式是成立的.

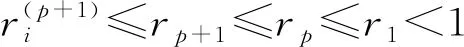
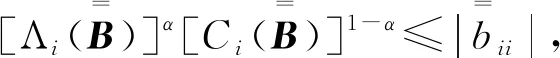
利用引理3,亦可得到下面的结论.

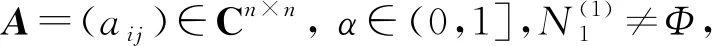
且至少有一严格不等式成立,又对每一个等式成立的i,存在非零元链aii1ai1i2ai2i3…aikj,满足:

2 数值算例

考虑矩阵

于是

致谢：本文得到内蒙古民族大学自然科学基金(NMDYB19057)项目的资助，在此表示感谢.