基于离散元法的分层施肥靴参数优化与试验
宋少龙 张东超 汤智辉 郑 炫 陈学庚,3 杨怀君 孟祥金
(1.石河子大学 机械电气工程学院,新疆 石河子 832000; 2.新疆农垦科学院 机械装备研究所,新疆 石河子 832000; 3.农业农村部西北农业装备重点实验室,新疆 石河子 832000)
施肥技术对提高作物肥料利用率具有重要意义[1-3]。目前我国农业生产主要以作物产量为目标,大量施用化肥是实现高产的主要途径,但由于施肥技术仍停留在地表分期撒施和全层施肥阶段,从而造成了肥料浪费及土壤板结[4-5]。张余莽等[6]指出我国目前化肥使用量是发达国家安全上限的1.93倍,但氮肥利用率比发达国家低20%~25%,磷肥钾肥利用率更低。
分层施肥技术是指将肥料按一定比例分层施于土壤中供作物在不同生长时期吸收,提高化肥的利用率[7-9],分层施肥技术依靠分层施肥装置实现。王云霞等[10]调整分层施肥器的安装角和施肥片调节装置的工作长度控制肥料配比和施肥量,通过台架试验,确定最优参数安装角为36°,工作长度13~16 mm;其田间试验表明,各层施肥量比例稳定,分层效果明显。姚万生等[11]设计一种可以将种子、种肥和基肥分别置于距地表5.3,11.5和17.6 cm,并且种肥和基肥的比例为3∶7的组合式下位分层施肥装置,保证不伤害种子、幼苗的同时也可以满足中、后期营养的供给。张小丽等[12]设计的双层施肥旋耕播种机,采用前后布置两套开沟器完成分层施肥作业。李辉等[13]设计一种将种子和化肥分别施于距地表5.4和11.0 cm处,种肥间层为5.6 cm的垂直分层种施开沟器。上述研究主要通过试验直接验证分层施肥装置的分肥效果,缺少对分层施肥结构的理论设计过程。化肥作为一种颗粒物料,与分层结构的碰撞接触会直接影响分层施肥装置的分层效果[14]。本研究基于化肥颗粒与分层施肥部件的相互作用,拟采用理论计算的方法设计一种新型分层施肥装置,用响应面分析法获得最有组合参数,并进行台架试验和田间试验验证,以期为分层施肥装置的设计研究提供参考。
1 分层施肥靴结构及原理
分层施肥靴结构主要由开沟器、分肥器和均肥器3部分组成(图1)。开沟器选用对土壤扰动较小的深松铲结构,由铲刃和铲柄组成。均肥器由圆管和周向均布、轴向等距的圆杆组成[15]。分肥器主要由分肥板、排肥板、挡泥板、排肥管和周围挡板5部分组成,分肥板顶部与上挡板相连,通过调整分肥板与均肥管轴线的径向距离,保证上下两层肥量比为4∶6,底部与排肥管进肥口端面相切,确保上下两层肥料不干涉。

1.开沟器;2.均肥器;3.上挡板;4.排肥板;5.分肥板;6.排肥管前挡板;8.侧挡板;9.挡泥板1.Furrower;2.Fertilizer uniform distribution device;3.Overhead baffle;4.Fertilizer discharging plate;5.Fertilizer separating plate;6.Fertilizer discharging tube;7.Front baffle;8.Side baffle;9.Fender图1 分层施肥靴总体结构Fig.1 General structure of layered fertilization boot
机具行进时,开沟器在土壤中开出30 cm的深沟,同时肥料沿导肥管以一定的初速度进入均肥器,肥料颗粒与圆杆发生碰撞和弹射后,下落形状由团聚状变为均布状,然后由分肥板按设计比例分成两份,下层肥料沿排肥板流出落在开沟器形成的沟槽,上层肥料沿排肥管流出落在回流土壤的表面,上下两层肥料实现分层。
2 分层施肥靴关键部件的理论设计
2.1 均肥器
肥料颗粒在均肥器中的运动过程见图2,肥料颗粒由导肥管进入均肥器与周向均布、轴向等距的圆杆发生碰撞、弹射,颗粒形态由团聚状变为均布状。
圆杆数量N和圆杆直径d分别决定了分肥份数2N和单层通过面积S[16]。肥料颗粒在均肥器的单层通过面积S为:
(1)
式中:D为均肥器内径,mm;d为圆杆直径,mm。均肥器中心交叠圆杆在圆管内形成的通过面积(即均肥器实际通过面积)Ssum为:
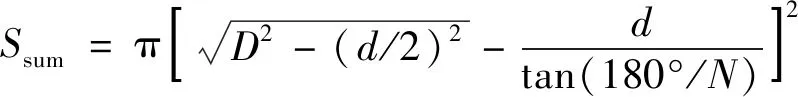
(2)
由式(2)可知,当圆管内径不变时,圆杆直径越大,数量越多,则Ssum越小,肥料颗粒在均肥器中的流通效率越低。
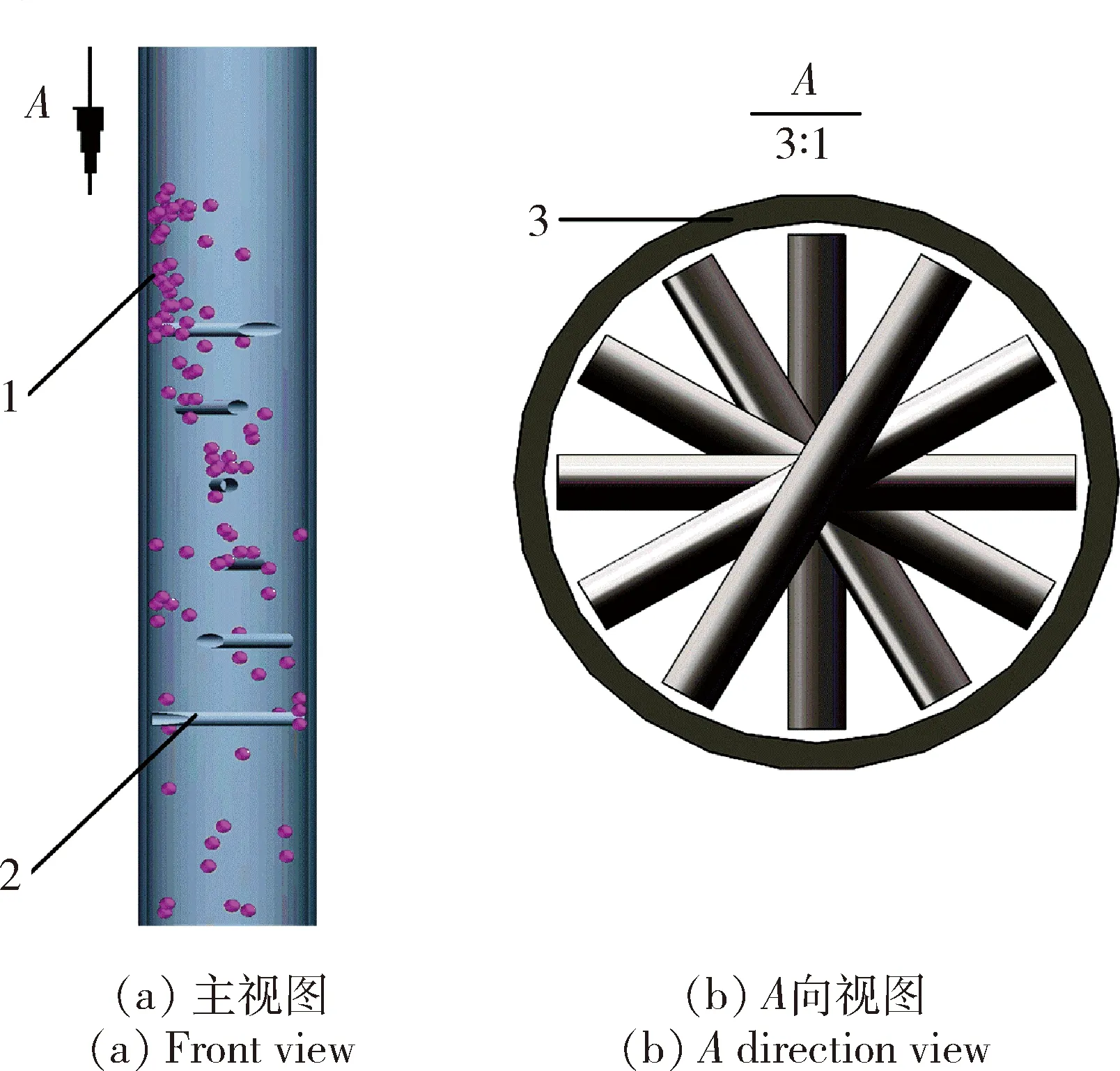
1.肥料颗粒;2.圆杆;3.圆管1.Fertilizer particle;2.Round bar;3.Tube图2 肥料颗粒运动轨迹与均肥器内部结构示意图Fig.2 Motion trajectory of fertilizer particles and schematic diagram of internal structure of fertilizer equalizer
根据我国新疆砂砾土质肥力情况,棉花和玉米每hm2最大施肥量为450 kg,作业速度最大值为7 km/h,排肥器单位时间排肥量151 g/s。外槽轮式排肥器的排肥舌距均肥器入口的距离为30 cm,设定肥料颗粒离开排肥舌时的初速度为0 cm/s,则肥料颗粒进入均肥器入口的速度为24.5 cm/s,肥料颗粒的堆积密度为0.877 g/cm3,均肥器不发生堵塞的最大流通面积为:
(3)
式中:Sthrough为最大流通面积,cm2;mt为单位时间施肥量,g/s;ρ为肥料颗粒的堆积密度,g/cm3;v为肥料流速,cm/s。
肥料颗粒由于重力作用在均肥器内竖直方向呈加速运动状态,当下肥量一定时,流速越大,通过面积越小。因此最大通过面积应采用肥料颗粒进入均肥器的初速度。根据肥箱的导肥管外径,设计圆管内径为38 mm,考虑到肥料的流通性和加工条件,选取圆杆直径最大为5 mm,圆杆数量最多为8根。由此计算得均肥器最小通过面积Ssum=20.99 cm2,单层最小通过面积S=9.44 cm2,均大于最大通过面积Sthrough=7.03 cm2,符合设计要求。
2.2 分肥器
分肥器肥料运动轨迹及分肥器结构见图3,肥料颗粒呈均布状由均肥器落入分肥器。肥料颗粒被均肥器下方的分肥板分成不同比例的上下两层,其上层落在排肥板形成加速下滑的颗粒流,与分肥板下端碰撞后,沿排肥管流出。下层肥料沿分肥板滑落到排肥板,在惯性的作用下与挡泥板发生碰撞,经下排肥口流出。最后在土壤回流作用下,肥料颗粒在土壤中形成两层。
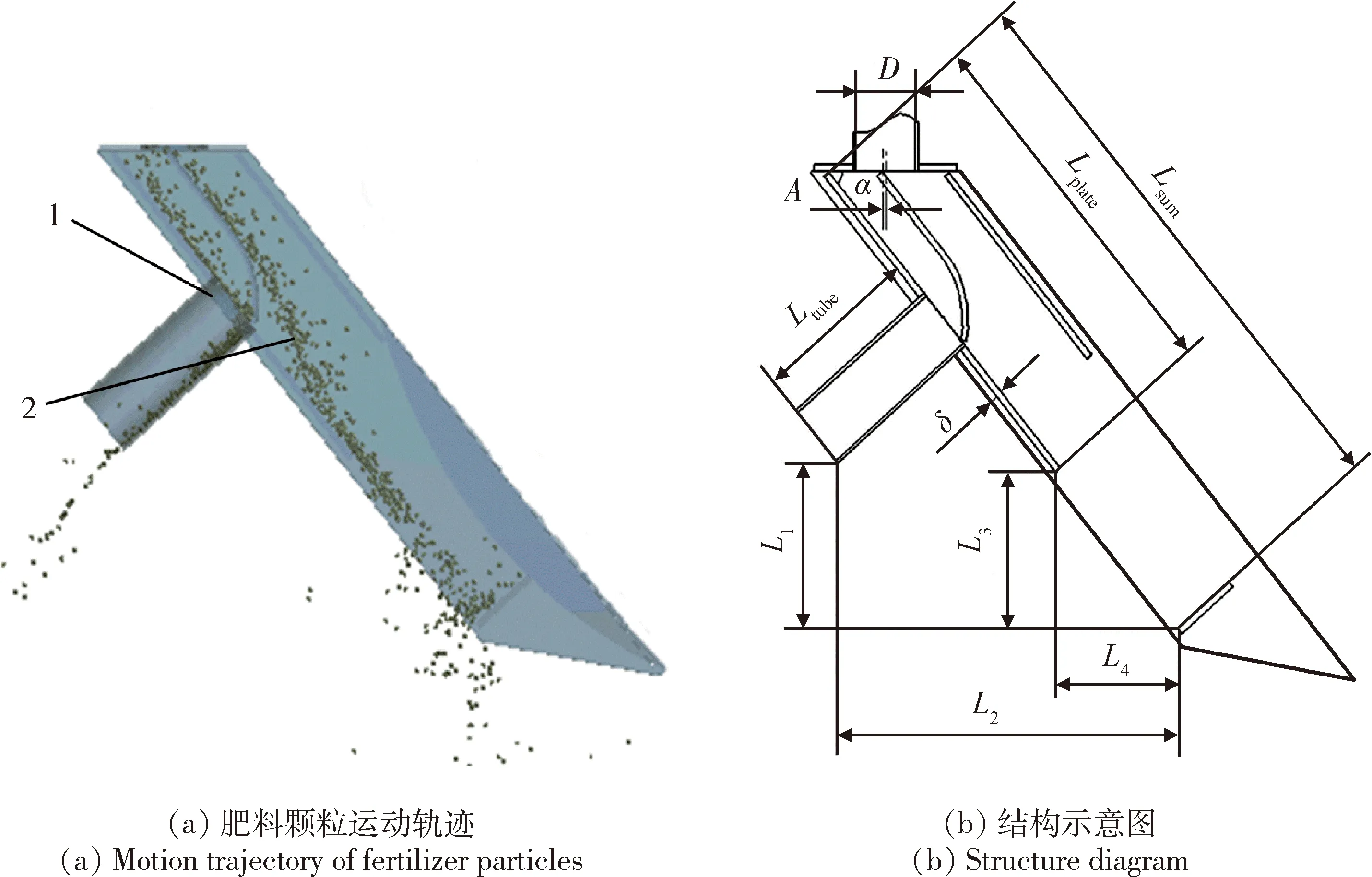
1.分肥器;2.肥料颗粒1.Fertilizer separating device;2.Fertilizer particleL1和L2分别为上下两层肥料出口的纵向和横向距离,mm;L3和L4为排肥板底端到下层肥料出口的纵向和横向距离,mm;α为分肥器倾角,(°);Ltube为排肥管长度,mm;Lplate为排肥板长度,mm;Lsum为排肥板顶端到挡泥板的对齐距离,mm;δ为排肥板厚度,mm;A为分肥板中心线与圆管中心线的距离,mm;D为圆管内径,mm。L1 and L2 are the vertical and horizontal distances of the fertilizer outlets in the upper and lower layers,mm;L3 and L4 are the vertical and horizontal distances of the bottom of the fertilizer exhaust plate to the fertilizer outlets in the lower layer,mm;α is the inclination angle of the fertilizer separator,(°);Ltube is the length of the fertilizer tube,mm;Lplate is the length of the fertilizer plate,mm;Lsum is the alignment distance from the top of the fertilizer plate to the fender,mm;δ is the thickness of the fertilizer plate,mm;A is the distance between the center line of the fertilizer plate and the center line of the round tube,mm;D is the inner diameter of the round tube,mm.图3 分肥器肥料运动轨迹及分肥器结构示意图Fig.3 Motion trajectory of fertilizer particles and structure of fertilizer separating device
肥料颗粒在分肥器中运动时,单个颗粒i的位移和运动方程为[17-20]:
(4)
(5)
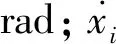
式(4)表示肥料颗粒新的位移值,将新的位移值代入式(5)得到新的作用力,反复循环即为单个颗粒i在分肥器中任意时刻的运动状态[21]。
排肥管和排肥板的长度决定上下两层肥料的相对位置。排肥管过长,处于土壤回流区域,容易发生堵塞。排肥管和排肥板过短,上下两层肥料出口的距离较近,分层效果不明显。排肥板过长,下排肥口较小,肥料颗粒与挡泥板发生碰撞回弹,影响施肥效率。
上下两层肥料出口的相对位置关系为:
(6)
式中:L1为上下两层肥料出口的纵向距离,mm;L2为上下两层肥料出口的横向距离,mm;L3为排肥板底端到下层肥料出口的纵向距离,mm;L4为排肥板底端到下层肥料出口的横向距离,mm;α为分肥器倾角,(°);Ltube为排肥管长度,mm;Lplate为排肥板长度,mm;Lsum为排肥板顶端到挡泥板的对齐距离,mm;δ为排肥板厚度,mm。
根据棉花和玉米施肥深度10~20 cm的要求,确保分层效果显著,选取Ltube=110 mm,Lplate=235 mm,Lsum=360 mm,α=50°,δ=2 mm,通过EDEM仿真检验肥料分层效果。
肥料颗粒经过均肥器后,其形态由团聚状变为均布状,分肥板中心线与圆管中心线的距离A控制着上下两层肥料在分肥器入口通过面积,即控制上下层肥量的比例,得到上下两层肥量比例为:
(7)
式中:Sup和Sdown分别为上下层肥料流入面积,mm2;A为分肥板中心线与圆管中心线的距离,mm;D为圆管内径,mm。
根据上下两层肥量比为4∶6的设计要求,即Sdown∶Sup=4∶6,得到分肥板中心线与圆管中心线的距离A=5.868 mm,为了减小比例误差,取分肥板的厚度为1 mm。
3 分层施肥靴参数优化仿真试验
分层施肥靴的结构决定肥料分层效果。对分层施肥靴进行三因素三水平的仿真试验,根据肥料分层效果优化最佳工作组合参数。
3.1 仿真参数设定
3.1.1全局变量参数设定
肥料颗粒、土壤和分层施肥靴的两两相互作用均采用Hertz-Mindlin模型[22-24],根据相关文献[25-30],确定仿真变量参数如表1所示。
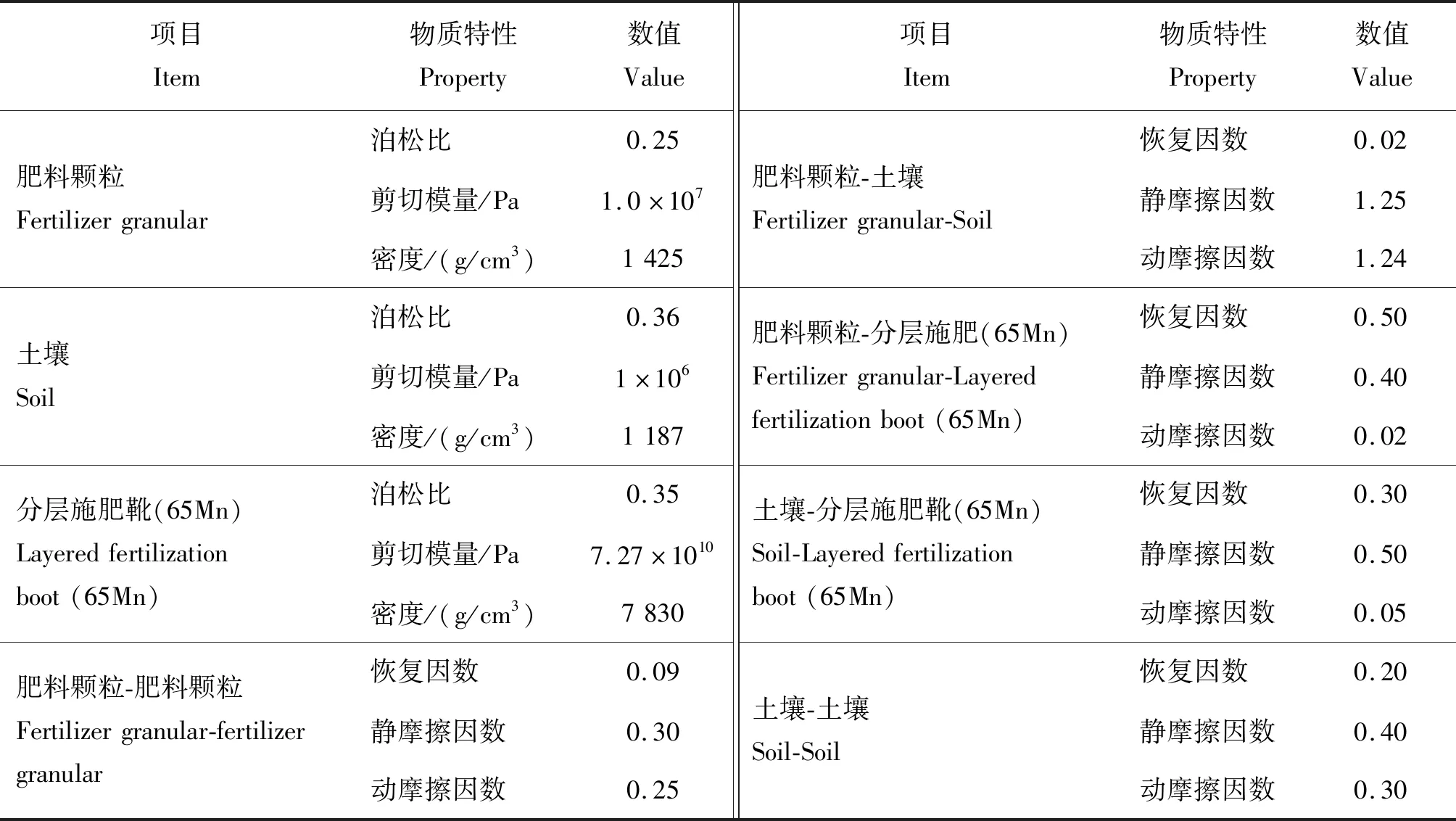
表1 仿真变量参数设置Table 1 Simulation variable parameters setting
3.1.2土壤、肥料颗粒建模
土壤颗粒的外形主要包括块状、核状和柱状3种[31]。通过前期对试验区域的土壤进行分级,60%以上的土壤属于粗砂粒(粒径1~0.25 mm),利用EDEM自带的颗粒单元生成土壤颗粒模型,如图4所示,建立1 500 mm(长)×200 mm(宽)×300 mm(高)的土槽模型,为了节省运算时间,将组成土壤颗粒的基体半径设置为3 mm,土壤密度设置为测量得到的1.187 g/cm3。肥料颗粒选用金屯农化磷酸二铵(金屯嘉吉三环肥料厂),对其三维尺寸进行测定,得到磷酸二胺颗粒的球形率为0.965,等效直径为3.56 mm,将肥料颗粒近似为圆形颗粒物体进行建模[30]。
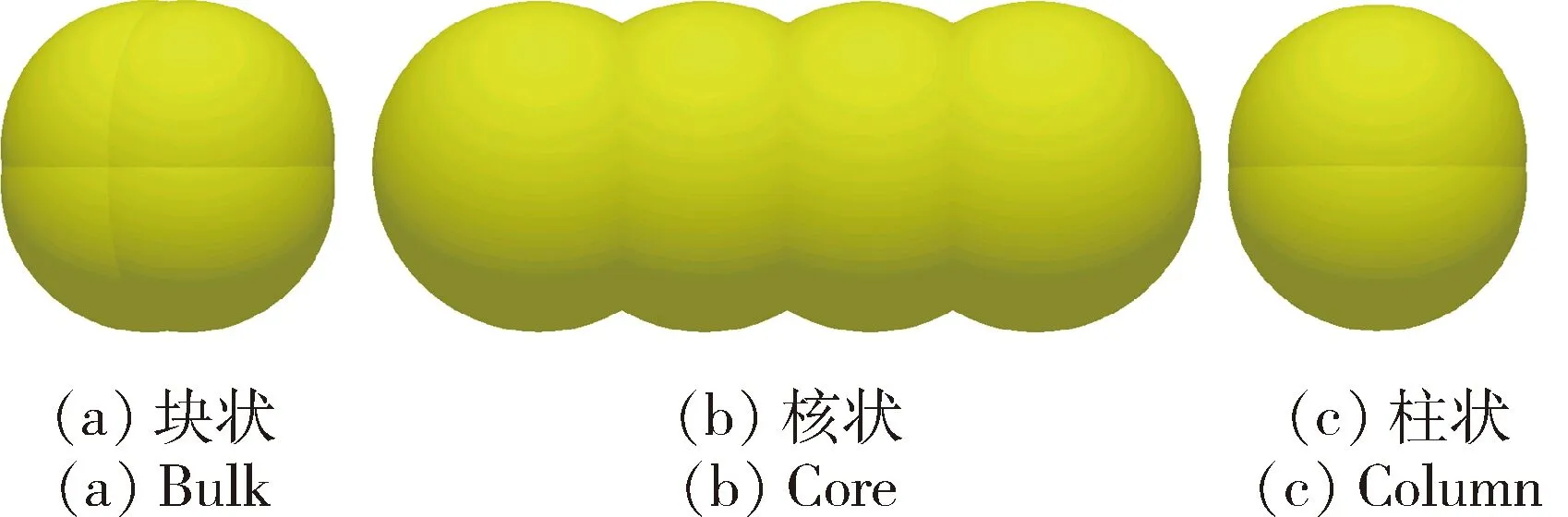
图4 土壤颗粒EDEN仿真模型Fig.4 Simulation model of edaphic particle
3.1.3仿真模型的建立
根据设计参数使用SolidWorks 2015对分层施肥靴按1∶1比例建模,将三维模型另存为.x_t格式导入EDEM中。按照表1设置仿真参数,在均肥器上方建立Polygon颗粒工厂,生成速率为515 g/s,下落初速度24.5 cm/s,总仿真时间为8 s,固定时间步长为Rayleigh时间步长的25%,数据记录间隔为0.1 s,分层施肥靴的仿真模型见图5。
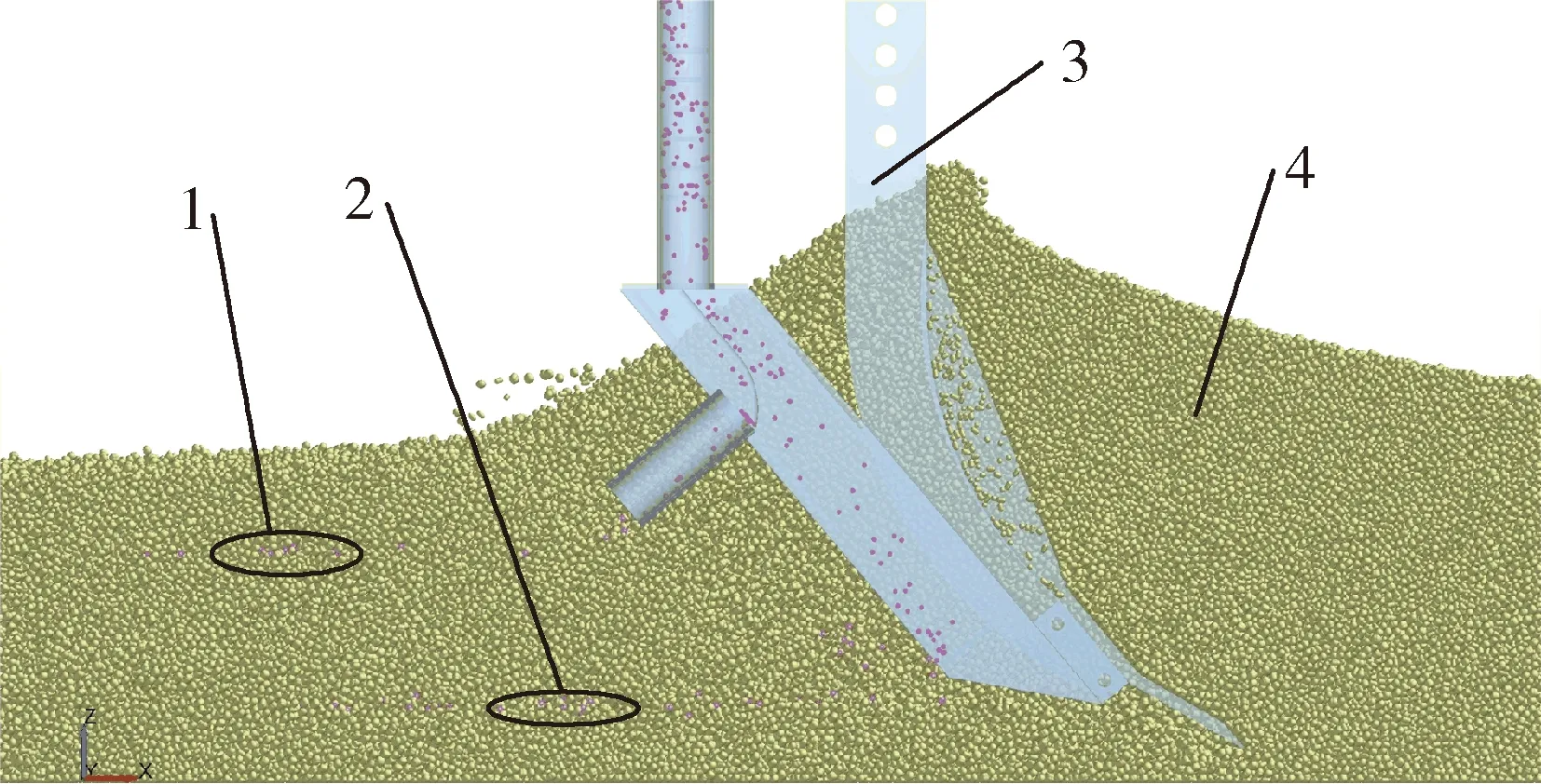
1.上层肥料;2.下层肥料;3.分层施肥靴;4.土壤颗粒1.Upper fertilizer particle;2.Lower fertilizer particle;3.Layered fertilization boot;4.Soil particle图5 分层施肥靴仿真模型Fig.5 Simulation model of layered fertilization boot
3.2 试验因素与指标
1)试验因素。主要影响因素有圆杆直径和圆杆数量。分肥器的排肥管和排肥板主要影响上下两层肥料的间隔距离,根据式(6)进行理论计算可直接设定,故分肥器不作为影响肥料分层的因素。分层施肥靴的行进速度影响土壤回流的快慢,直接关系到肥料的分层效果,故本研究以圆杆直径,圆杆数量以及分层施肥靴的行进速度作为影响因素。
2)试验指标。用上下两层肥料间隔距离的变异系数Cv作为考察指标反映肥料的分层效果。试验中,通过测量分层施肥靴行进过后同一纵截面上下两层肥料的中心距,计算上下两层肥料距离的变异系数。变异系数计算公式为:
(8)
式中:SSD为同一纵截面上下两层肥料距离的标准差,cm;Smean为同一纵截面上下两层肥料距离的平均值,cm。
3.3 试验设计
根据前期相关试验得到各变量的变化范围,选取圆杆直径4 mm、圆杆数量6根和行进速度 6 km/h 为零水平,以上下两层肥料距离的变异系数为评价指标(表2)。采用响应面法分析3个因子对响应值(上下两层肥料距离的变异系数)的影响程度,得到分层施肥靴的最佳组合参数。
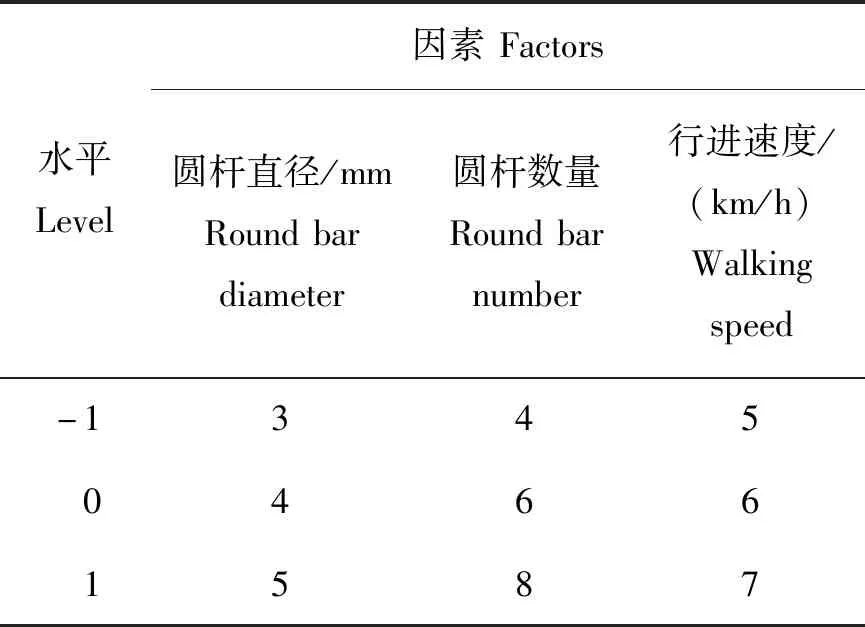
表2 响应面因素水平表Table 2 Factors and levels of RSM analysis
3.4 结果分析
3.4.1回归模型的建立与检验
采用Design-Expert.V10.0.3的Box-Behnken模块进行三因素三水平的试验设计[33],试验结果见表3。根据显著性检验,模型的F值为33.87,P<0.01,表眀该模型极显著。变异系数模型的决定系数R2=0.9775,证明该模型拟合程度良好。上下两层肥料距离变异系数的回归方程为:
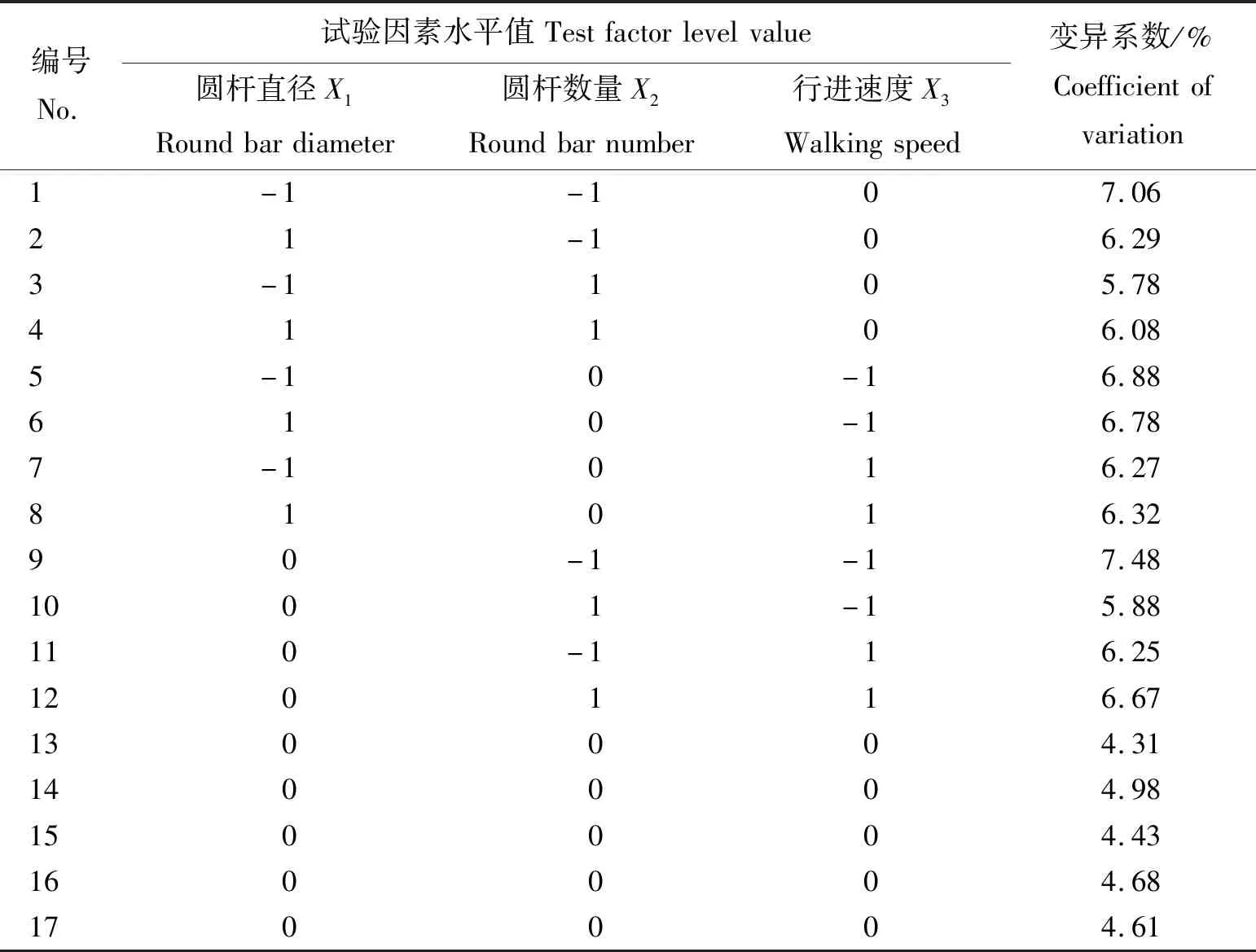
表3 仿真试验方案及结果Table 3 Simulation test plan and results
Y=4.60-0.07X1-0.33X2-0.19X3+
0.27X1X2+0.04X1X3+0.50X2X3+
0.85X12+0.85X22+1.11X32
(9)
式中:X1、X2和X3分别为圆杆直径、圆杆数量和行进速度的水平编码;Y为上下两层肥料距离变异系数,%。
由回归方程系数的绝对值大小得到各因素影响程度主次顺序为圆杆数量>施肥靴行进速度>圆杆直径。对式(9)所表示的回归方程进行方差分析,分析结果见表4。
3.4.2两因素对变异系数的影响
由表4可知,圆杆直径和圆杆数量的交互作用对上下两层肥料距离变异系数的影响显著,而圆杆数量和分层施肥靴行进速度的交互作用对上下两层肥料距离变异系数的影响极显著,因此对圆杆数量和分层施肥靴的行进速度对上下两层肥料距离变异系数的影响进行响应曲面分析,结果见图6。
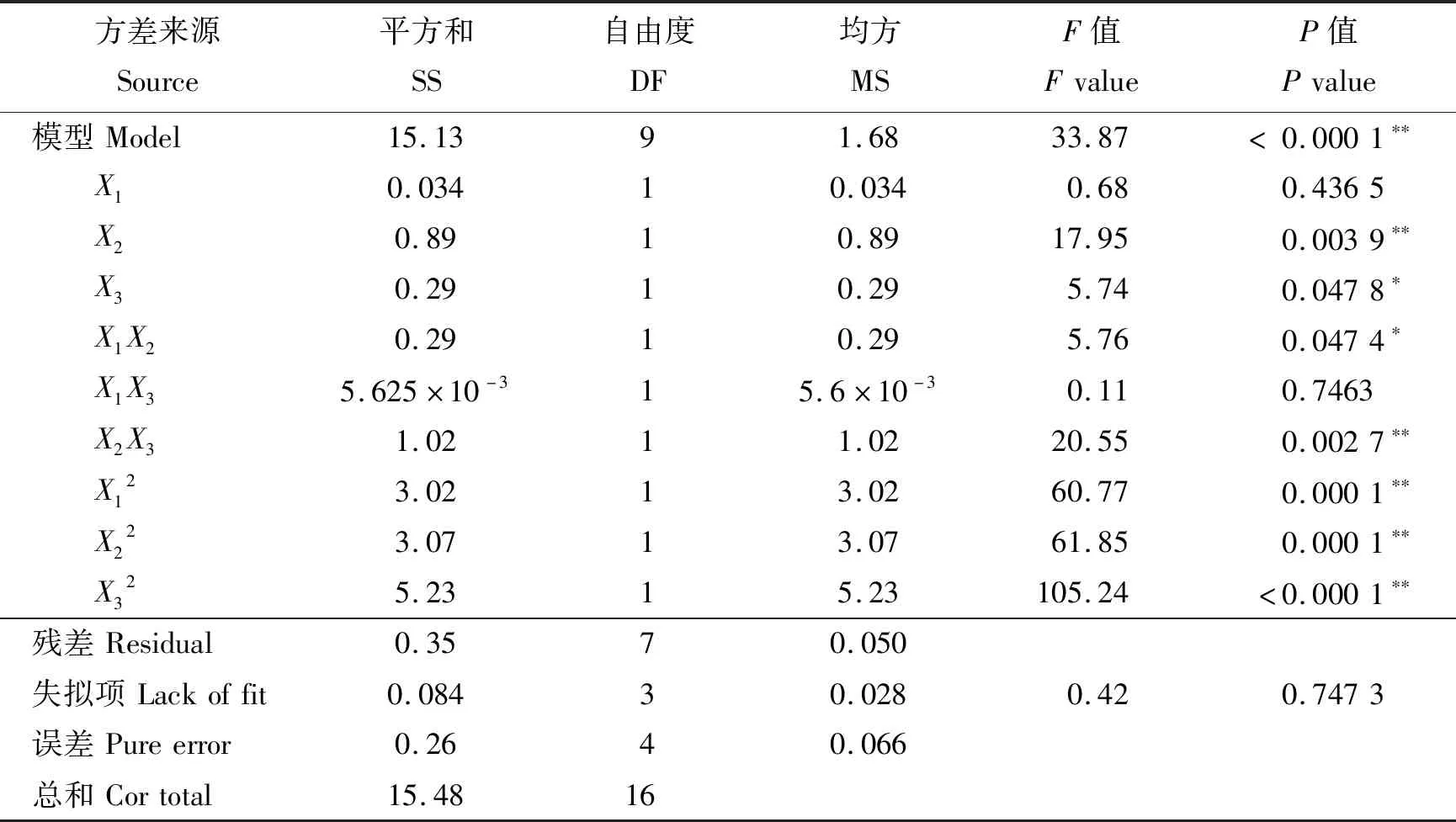
表4 上下两层肥料距离的变异系数回归模型方差分析Table 4 Analysis of variance for regression model of coefficient of variation of fertilizer distance between upper and lower layers
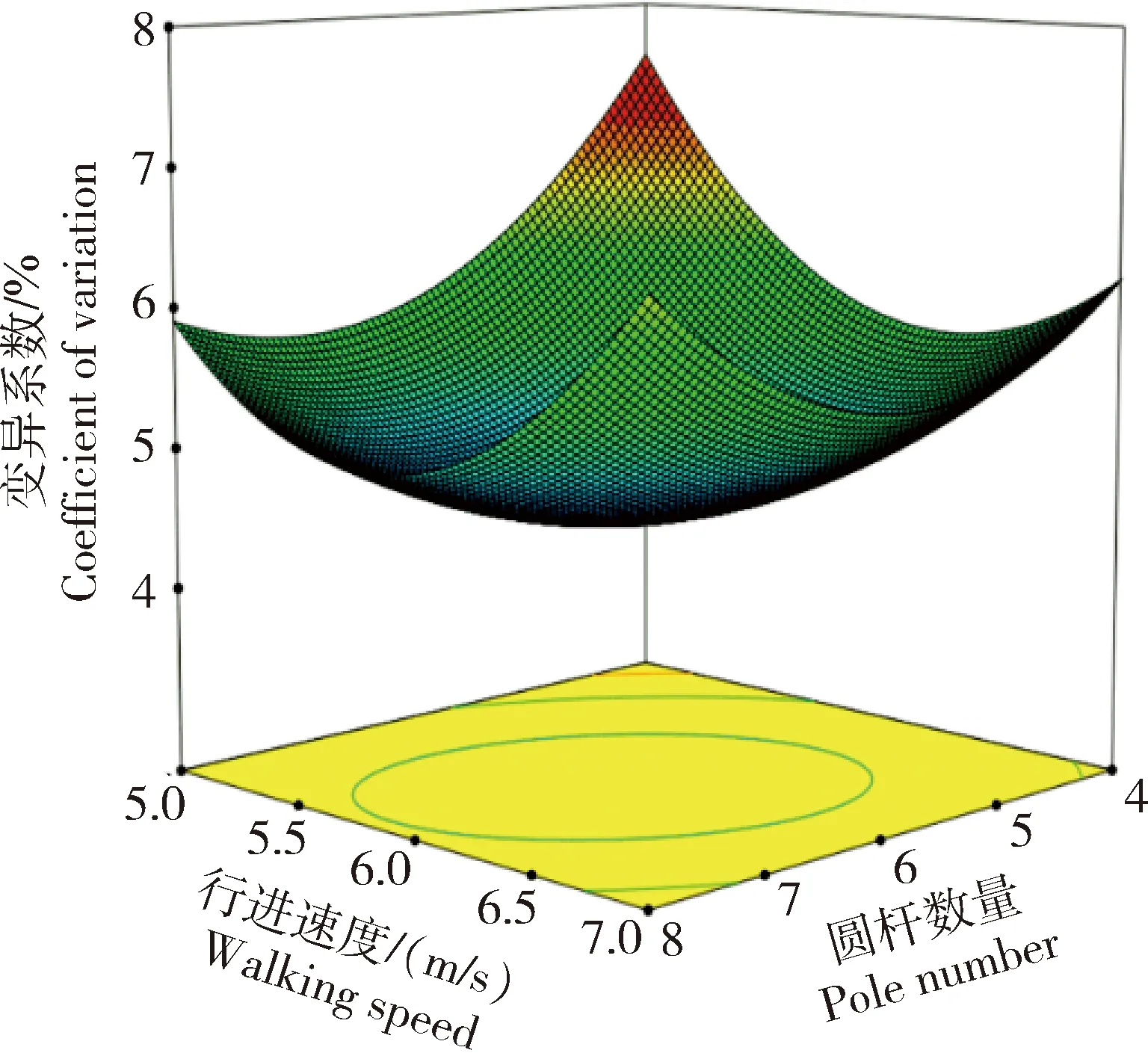
图6 施肥靴行进速度和均肥器圆杆数量对变异系数的影响Fig.6 Effects of travel speed of layered fertilization boot and pole number of fertilizer equalizer on coefficient of variation
可见,圆杆数量和分层施肥靴的行进速度两因素的响应面为开口向上的抛物曲面。圆杆数量在低水平时,分层施肥靴的行进速度对上下两层肥料距离的变异系数的影响极显著,表现为响应面抛物曲线比较陡,说明在圆杆数量较少时,增加分层深施机构的行进速度能明显降低上下两层肥料距离的变异系数。而在圆杆数量较多时,分层施肥靴的行进速度对上下两层肥料距离的变异系数的影响不是很明显,表现为响应抛物曲线比较平缓,这表明圆杆数量和分层施肥靴的行进速度存在一定的交互作用,同时根据方差分析可知二者的交互作用为极显著[34]。
3.4.3分层施肥靴参数优化
为确保施肥靴具有更好的分层效果,本研究以上下层肥料距离的变异系数为分层目标,进行分层施肥靴工作参数和结构参数优化,利用Design-Expert.V10.0.3软件中的Optimization-Numerical模块进行优化求解,其目标函数与约束条件为:
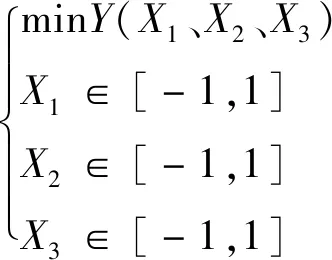
(10)
根据上下两层肥料距离的变异系数越小越好的原则,优化后得到影响因素最佳区域,通过Design-Expert.V10.0.3选取最佳参数组合为:圆杆直径4 mm,圆杆数量6根,分层施肥靴的行进速度6.04 km/h,此条件下上下两层肥料距离的变异系数为4.57%。
4 验证试验
通过理论计算分肥器中肥料颗粒的流通面积,将上下层肥量比固定为4∶6,但经过均肥器的肥料颗粒必须为均布状才能实现按比例分层,故对均肥器进行仿真试验,观察肥料颗粒的分布状态,利用台架试验实测上下层分肥比例,最后由田间试验观察肥料颗粒在土壤中的分层效果。
4.1 台架试验
通过台架试验对上下排肥口的肥量进行实测验证。试验地点为新疆科神农业装备科技开发股份有限公司的装配工厂;试验材料选用金屯农化磷酸二铵;试验装置见图7,主要包括直流电机(1016Z1B型,豫鑫电机公司)、12 V直流电机调速控制器(12-2*500全功能型,豫鑫电机公司)、分层施肥靴(圆杆数量为6根,圆杆直径为4 mm)。

1.肥箱;2.调肥手轮;3.直流电机;4.分层施肥靴;5.12V直流电机调速控制器;6.上层肥料收纳袋;7.下层肥料收纳袋1.Fertilizer can;2.Fertilizer handwheel;3.DC motor;4.Layered fertilization boot;5.12 V DC motor speed controller;6.Upper fertilizer storage bag;7.Lower fertilizer storage bag图7 上下层肥量比测定台架试验装置Fig.7 A bench test device for the determination of the fertilizer ratio of the upper and lower layers
使用直流电机进行分层施肥靴行进速度的模拟;用调肥手轮进行施肥量的调整;使用接肥袋分别收集上下两层肥料并称重计算出其占比。试验按施肥量(20、25、30 kg)分成 3个大组,每个大组又根据行进速度(5、6、7 km/h)各分成3个小组,每个小组进行10次试验取其平均值,试验结果见图8。试验结果表明:根据理论计算获取的均肥器结构参数可以保证肥料颗粒顺畅流动,施肥量和分层施肥靴的行进速度对上下层肥量比的影响甚微,分层施肥靴满足上下层肥量比4∶6的设计要求。
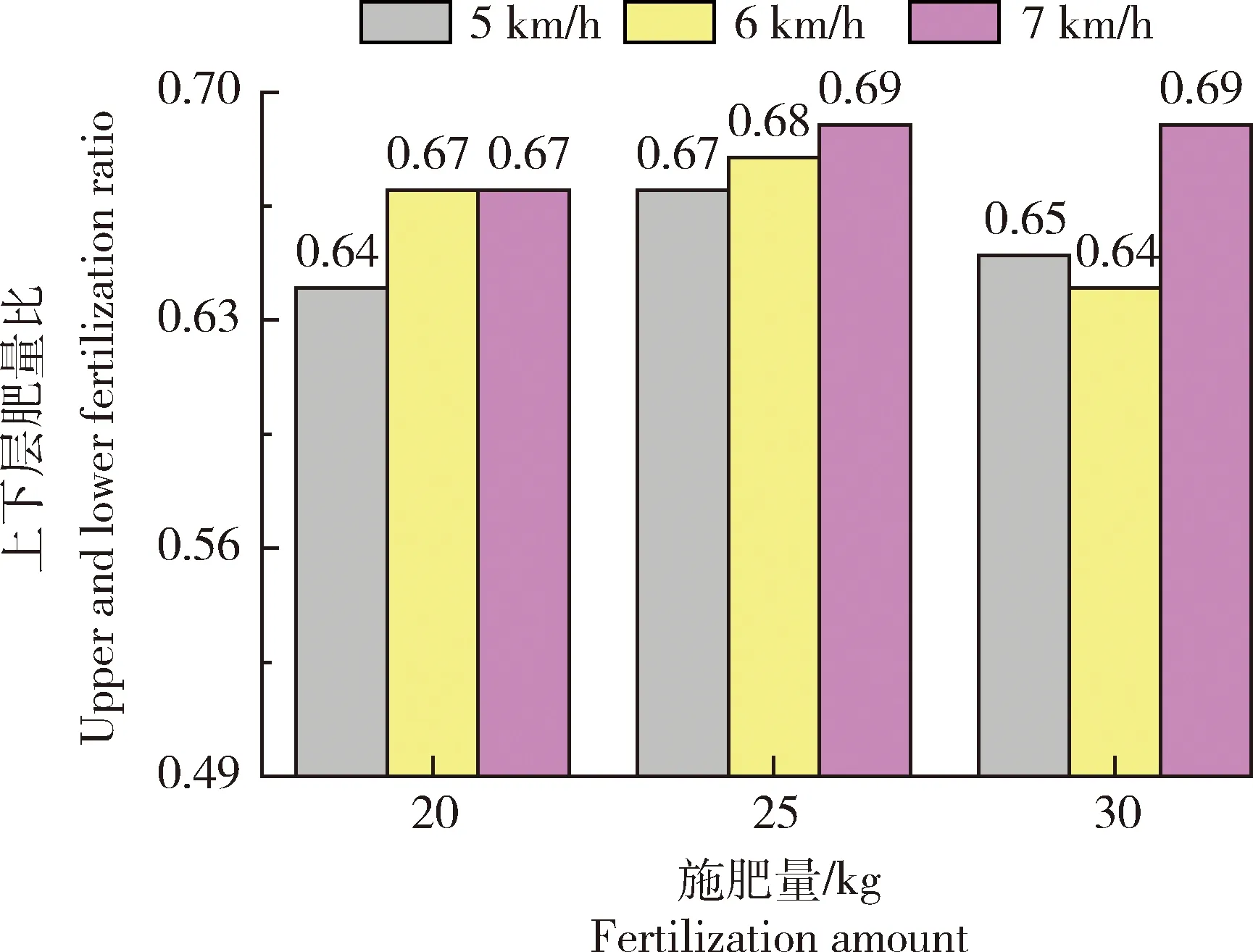
图8 3种速度不同施肥量下施肥靴上下层肥量比Fig.8 The ratio of the upper and lower layers of the boots with different fertilization rates
4.2 田间试验
为了验证离散元仿真试验所得最优组合参数及分层施肥靴的工作性能,在不同施肥量条件下,比较仿真试验与田间试验上下两层肥料距离变异系数的相对误差。试验地点为伊宁县青年农场,试验区域土壤粒级为粗砂粒,密度1.187 g/cm3,含水率14.726%,坚实度0.57 MPa。试验材料为金屯农化磷酸二铵;试验装置主要包括雷沃欧豹TG125型拖拉机、安装分层施肥靴的分层施肥机等(图9)。根据仿真试验结果,分层施肥靴圆杆数量选用6根,圆杆直径4 mm,机具行进速度设为6.04 km/h。

图9 分层施肥机与分层施肥靴Fig.9 Layered fertilizer applicator an layered fertilizer boots
田间试验和仿真试验肥料分层效果比对(图10)显示,2种试验均实现了肥料颗粒的上下分层且效果明显,满足设计要求。施肥量20 kg时肥料颗粒在土壤中的位置分布情况见图11,仿真试验和田间试验都存在一定的波动性,波动都不超过预设的幅度范围,上层肥料位于距地表10~15 cm,下层肥料位于距地表15~20 cm,上下两层肥料间隔在5 cm左右,肥料分层效果显著。
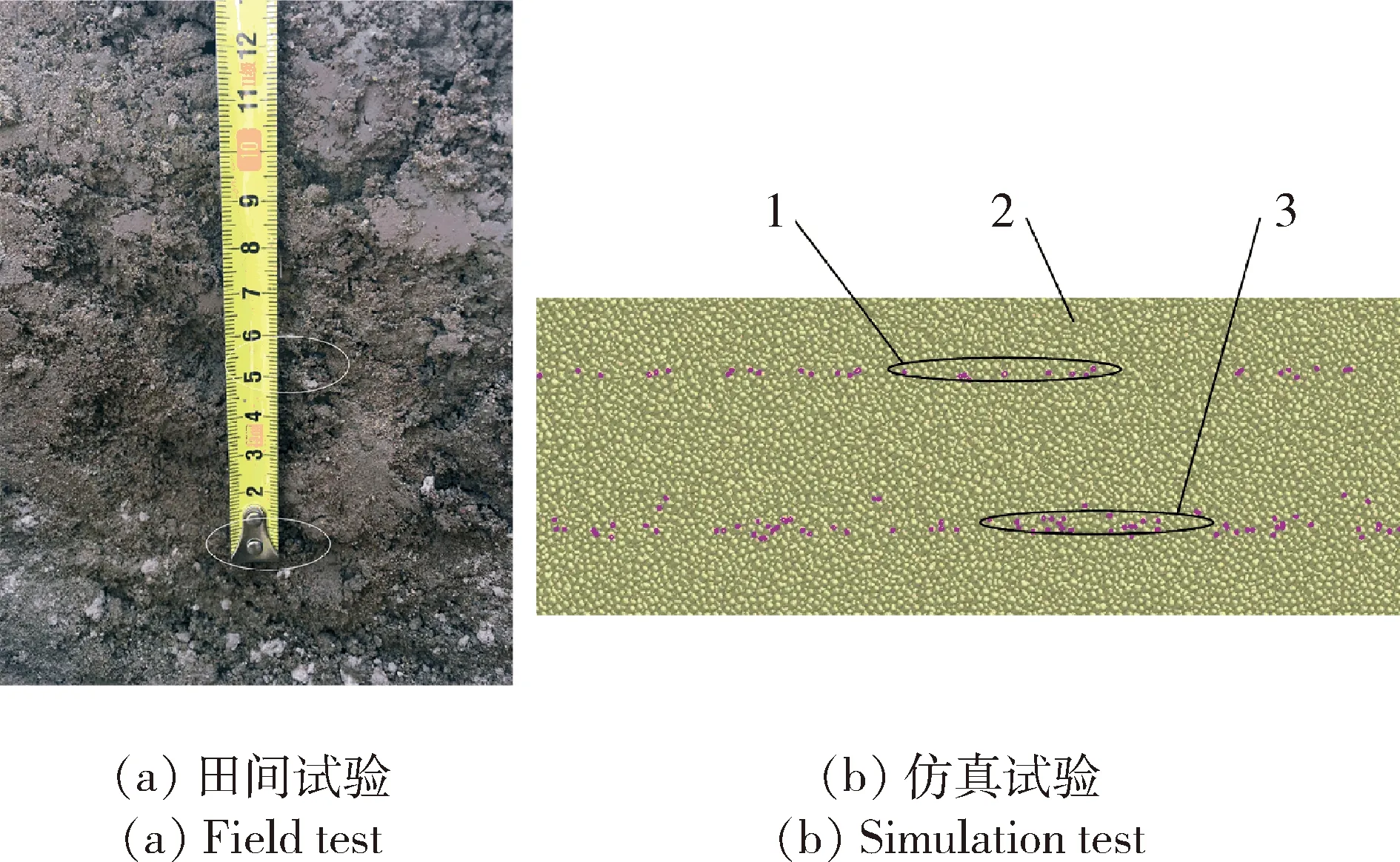
1.上层肥料;2.土壤颗粒;3.下层肥料1.Upper fertilizer particle;2.Soil particle;3.Lower fertilizer particle图10 田间试验与仿真试验肥料分层效果对比Fig.10 Comparison of fertilizer stratification effect between field test and simulation test
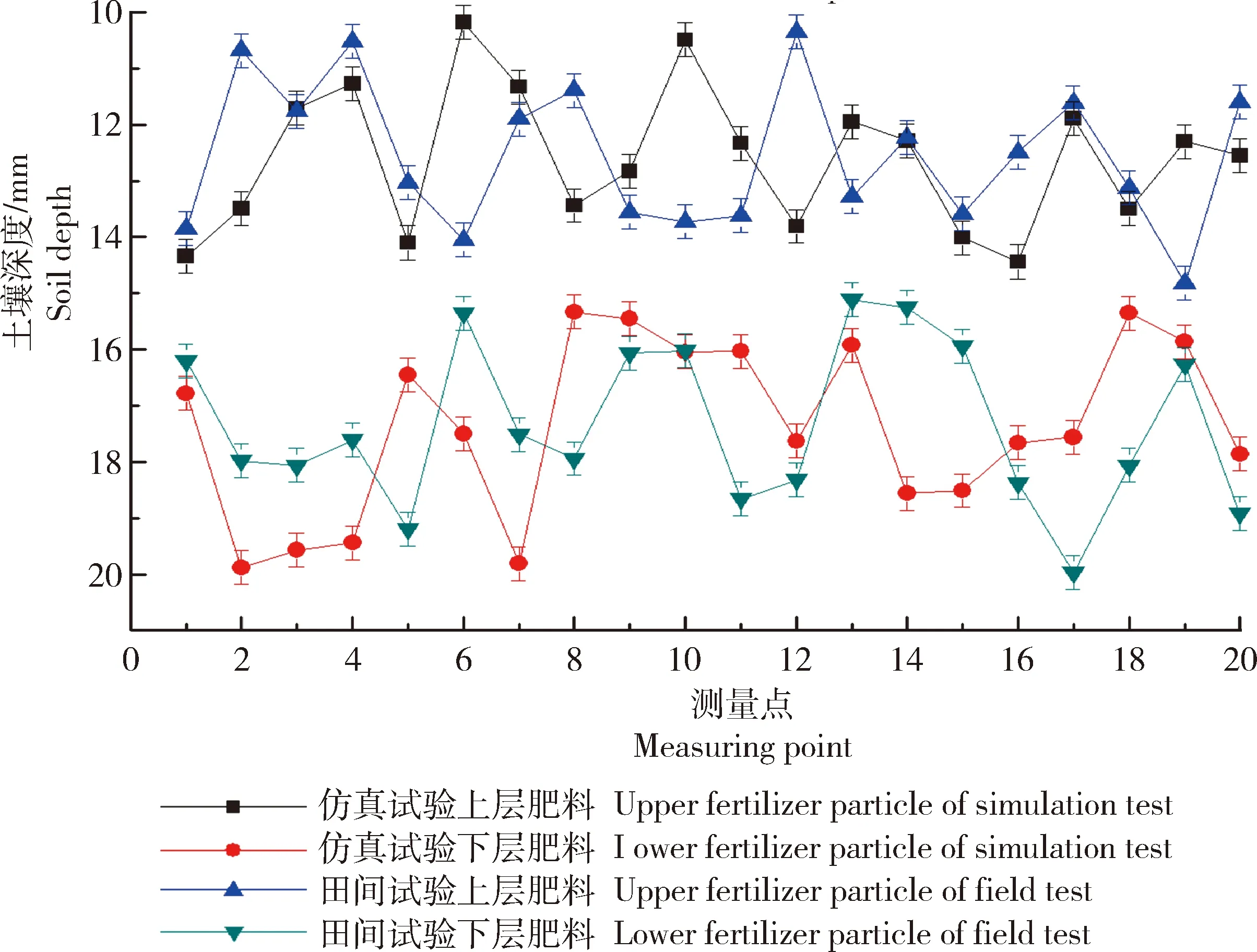
图11 施肥量20 kg肥料颗粒分布位置Fig.11 Fertilizer distribution locations of 20 kg fertilizer granules
测量不同施肥量条件下田间试验和仿真试验中上下两层肥料间隔距离的变异系数见表5。可以看出变异系数的仿真结果比试验结果略大,相对误差不超过4%,而且具有相同趋向,施肥量越大,肥料颗粒越多,分层更为明显,故上下两层肥料间隔距离的变异系数越小。证明离散元仿真可以很好地辅助关键部件的设计与优化。

表5 仿真试验与田间试验上下层肥料距离变异系数相对误差Table 5 Relative error of the coefficient of variation of the distance between the top and bottom layers of the simulation test and the field test
5 结论及讨论
1)本研究设计了一种分层施肥靴,以上下两层肥料间隔距离的变异系数为分层目标,对EDEM仿真试验数据通过Design-Expert.V10.0.3软件处理及优化,分层施肥靴最优组合参数为:圆杆数量6根,圆杆直径4 mm,分层施肥靴行进速度6.04 km/h,此时变异系数为4.57%。
2)选用最优组合参数的分层施肥靴进行台架试验和田间试验,并与仿真试验进行对比,结果表明,在不同施肥量条件下,分层施肥靴均有较好的肥料分层效果,仿真值与试验值的相对误差不超过4%,分层效果基本吻合,施肥效果稳定,说明利用离散元仿真试验对分层施肥装置进行优化具有可行性。
由于化肥种类繁多,物料特性存在一定差异,因此本研究中的分层施肥靴试验装置的试验对象为物料特性与磷酸二铵类似的化肥,以实现分层施肥的目的。机具在作业过程中,经过土壤条件较差的区域时,在下排肥口有土壤粘黏,并且施肥靴行进阻力略有增加,分析原因有:施肥靴机构存在不足,需进一步优化;施肥靴材料方面的原因;土壤黏度较大,前期整地效果不好。后续将进一步对影响施肥靴土壤粘黏和减阻性能的因素进行研究。

