插座阀芯关闭过程内部流场数值模拟研究

符耀民，罗卫东，2，贺迪华，赵飞虎

（1．贵州大学机械工程学院，贵州 贵阳 550025；2.贵州大学明德学院，贵州 贵阳 550025）

1 引言

分离接头在航天器级间分离过程中起着快速断开管路且在正常工作状态下接通管路和传递介质。由于插座分离过程需要在短时间内完成且在分离结束后留在航天器上起着密封管路的作用，为满足插座阀芯能在短时间内关闭且降低其正常工作状态下的稳态阻力损失，因此对插座阀芯不同开度下的稳态和关闭过程中的内部流场进行数值模拟。

目前，运用动网格技术对阀类的研究已取得了显著的成果。文献[1]运用Fluent 动网格技术对电磁阀阀芯的开启过程进行仿真研究，得到开启过程中作用在阀芯上的轴向气动力的变化规律；文献[2]应用Fluent 动网格技术分析了球阀不同启闭规律、阀腔大小等因素对球阀流场动态特性的影响；文献[3]采用动网格技术对弹簧式灌水器流场进行数值模拟，将计算值与试验值进行对照分析，获得水头损失、上下游压差力合流量之间的关系；文献[4]应用泵阀仿真软件PumpLinx 的动网格技术对单向阀三维动态流场的稳定性进行了仿真研究，得到了不同工作压力、质量流量条件下的单向阀动态稳定特性。

上述对阀类的内部动态流场均有一定的研究，但大多数模拟情况下阀芯的运动速度为一常值，并不能很好的描述实际运动过程。运用用户自定义函数（UDF）对阀芯运动过程的内部流场进行模拟，能够很好的反应实际运动过程。

2 物理模型

插座全开状态下的结构，如图1（a）所示。在阀芯顶端失去支撑和在复位弹簧的作用下阀芯向左移动，此时阀芯将通路截断从而关闭插座。阀芯全开状态下的ΔL=19.9181mm，建立阀芯不同开度下的几何模型。阀芯全开状态下插座流场的几何模型，如图1（b）所示。

图1 插座结构及其流域模型Fig.1 The Socket Structure and its Basin Model

插座阀芯在关闭过程中受到弹簧力、液动力和黏性阻力三者的共同作用，由于介质的黏度较小，忽略黏性阻力，因此在插座的设计过程中弹簧力和液动力的计算就变得尤为重要。利用Hooke 定律可以确定弹簧力，而作用在阀芯上的液动力难以用解析法求得；运用Fluent 软件对适当简化的原始和改进阀芯的插座3D 模型进行数值模拟，得到关闭过程中作用在两种阀芯上的液动力和内部流场情况，同时计算了不同开口条件下的稳态液动力和流阻情况，如图2 所示。

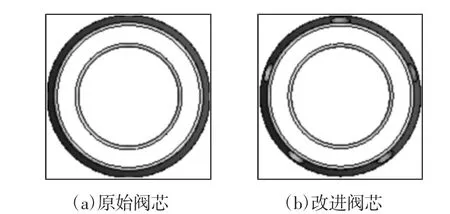
图2 两种阀芯结构Fig.2 Two Valve Core Structures

3 数值方法及边界条件

3.1 控制方程

考虑由移动边界∂V 所包含的任意控制体内积分形式的非定常不可压黏性流体的体积守恒方程、质量守恒方程和动量守恒方程[5-6]：

3.2 数值求解方法

3.3 动网格生成方法

考虑到插座阀芯关闭过程运动距离较长，又由于非结构化网格具有对复杂边界良好的适应性且很容易通过细分或者重新生成网格的方法实现自适应过程[7]；采用弹簧光顺和局部网格重构相结合的方法实现对动网格的更新。弹簧光顺法是在网格弹性变形过程中，将连接节点的网格边近似的看做一受力的弹簧，初始网格的分布为平衡状态，边界网格点的位移使其与之相连的连线上产生相应的弹性应力；此弹簧受力满足Hooke 定律，即：

运用弹簧光顺法可以模拟小变形时的流场网格节点位置，但当网格发生大变形时会导致网格质量下降，或出现负体积而导致网格更新失败，为确保计算过程中的网格质量，需要结合局部网格重构法对网格进行重新生成[8]。

3.4 计算边界条件

选择非稳态求解器模型时，由于Realizable k-ε 湍流模型的仿真结果与实验值结果吻合程度较好[9]，故采用Realizable k-ε 湍流模型、配合标准壁面函数对滑块流域进行仿真计算；流体介质选为MMH，密度为874.4kg/m3，动力粘度为7.75×10-4Pa·s，操作压力为101.325×10-3Pa，设置入口速度为3.2148m/s，出口压力为3.40MPa。对流项采用二阶迎风格式，压力项采用PRESTO! 格式，扩散项采用中心差分格式，压力-速度耦合方程采用SIMPLE 算法。将阀芯设置为刚体，采用Fluent 中UDF 的预编译宏DEFINE_CG_MOTION来定义其运动规律。UDF 函数中主要通过式（9）来控制阀芯运动，即：

相接触插头的质量0.1574kg。

由于运动速度较大，考虑到每个计算步内阀芯与壁面的距离和网格的更新速度，选择时间步长Δt=6.4721×10-6s。

4 不同开度下的稳态结果分析

阀芯的开度由ΔL 来控制，取ΔL 值为0.0266mm、0.3621mm、1.0295mm、1.6903mm、2.6688mm、4.8865mm、7.2928mm、16.5756mm和19.9181mm 进行稳态结果分析。

4.1 不同开度下流阻情况

不同开度下两种阀芯结构的入口到出口压降ΔP 以及出口平均流速u2，如表1、表2 所示。由式（10）即可计算出不同开口度下的阻力水头损失hw。

表1 原始阀芯计算数据Tab.1 The Data of Calculation Results for the Original Valve Core

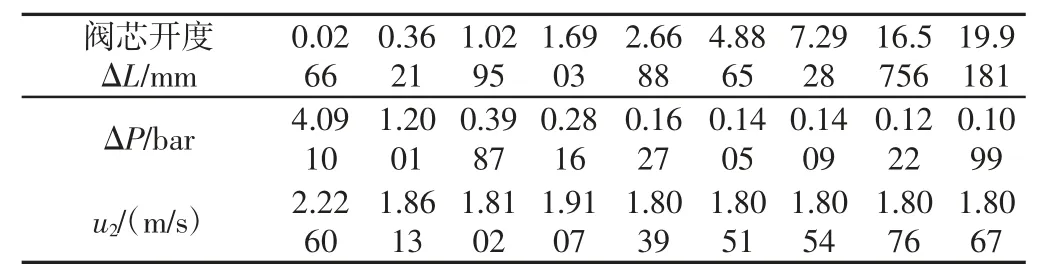
表2 改进阀芯计算数据Tab.2 The Data of Calculation Results for the Improved Valve Core

由黏性流体总流的伯努利方程可计算出hw，即：

式中：ΔP—入口到出口压降；

u1—入口速度；

u2—出口速度；

ρ—MMH 密度；

g—重力加速度；

α1、α2—动能修正系数，一般近似取为1。

将上述不同开度下计算出的阻力水头损失hw连成曲线，如图3 所示。由图可知，随着阀芯开度ΔL 的减小，hw先经过一段平缓增加过程，到达开度约为1.25mm 时，hw增加速度迅速提升，由此可知，开度越大对降低流阻损失越有利；相比两种阀芯结构，改进后的阀芯所在流域的阻力水头损失总是略低于原始的阀芯所在流域的阻力水头损失。

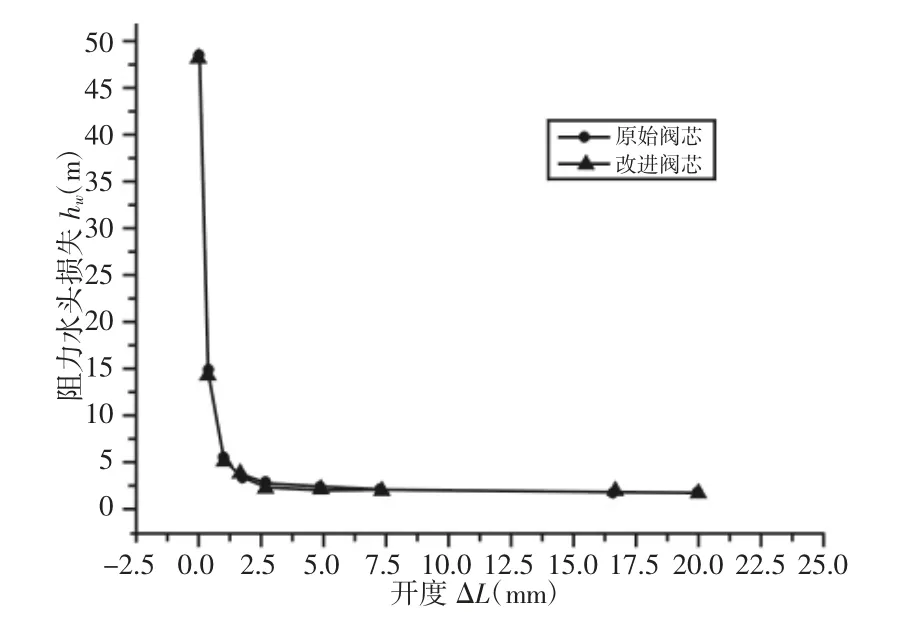
图3 两种阀芯结构下的hw/ΔL 曲线Fig.3 Curves of hw/ΔL for Two Types of Valve Core

4.2 不同开度下稳态液动力

稳态液动力是指阀芯移动到平衡位置时，流体因动量改变而附加作用在阀芯上的力[10]。在不同固定阀芯开度ΔL 下，由Fluent 软件中的表面积分功能，即可算出两种阀芯结构因动量变化而附加作用在阀芯上的力，如图4 所示。图4 中稳态液动力为负值代表方向朝着y 轴的负方向，从图中可知，两种阀芯所受到的稳态液动力均随开度ΔL 的减小而增加，在阀芯开度为1.25mm左右，阀芯液动力出现突变的转折点，并且随着开度的进一步减小，稳态液动力迅速增加；同时也可以看出，改进的阀芯所受到的稳态液动力总是小于原始阀芯的稳态液动力。

图4 两种阀芯结构下的稳态液动力F/ΔL 曲线Fig.4 The Steady-State Hydrodynamic Force Curves of F/ΔL for Two Types of Valve Core

5 插座关闭过程结果分析

5.1 网格的移动

插座阀芯运动过程中瞬时移动的计算网格，如图5 所示。初始计算网格，如图5（a）所示。阀芯运动到3.8833ms 时的计算网格，如图5（b）所示。阀芯运动到5.1777ms 时的计算网格，如图5（c）所示。阀芯运动到6.6663ms 时即将关闭的计算网格，如图5（d）所示。可以看出，采用此方法能够很好的描述阀芯的运动。

图5 不同时刻的计算网格Fig.5 Compute Mesh at Different Times

5.2 插座内流场的压力分布

两种插座阀芯（左为原始阀芯，右为改进阀芯）运动过程中不同时刻的流场压力分布图，如图6 所示。从图中可以看出，不同时刻，插座内流场的压力分布有所变化，当阀芯开度相对较大时，两种插座阀芯内流场的压力分布基本一致，均在喉部拐角处出现负压区。当阀芯开度逐渐减小时，两种插座阀芯的内流场压力分布区别也越来越明显，尤其到阀芯即将关闭的过程，原始阀芯的插座内流场压力分布更不均匀，且在阀芯斜面与壁面之间形成一个封闭腔导致压力急剧上升，严重阻碍阀芯的关闭；而改进的阀芯在其上开有5 个通孔，有效地改善了阀芯即将关闭过程中出现的上述现象。

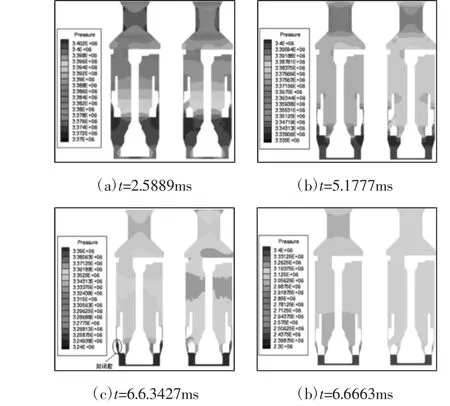
图6 不同时刻的压力分布Fig.6 Pressure Distribution at Different Times

5.3 阀芯关闭过程中的瞬态液动力

瞬态液动力是阀芯在移动过程中（即开口大小发生变化时）插座内液流因加速或减速而作用在阀芯上的力；这个力只与阀芯移动速度有关（即与阀芯开口度的变化率有关），而与阀芯的开口度本身无关[11]。根据阀芯在关闭过程中所受到的压力与阀芯在不同开度静止时的压力差值，即可得到瞬态液动力。

两种阀芯结构在插座关闭过程中所受到的瞬态液动力曲线，如图7 所示。从图中可以看出，两种阀芯结构所受到的瞬态液动力大致趋势基本一致，随着阀芯的运动，所受到的瞬态液动力首先以平缓的趋势增加；当运动接近6.50ms 左右时，阀芯所受到的液动力迅速增加，此过程是由于阀芯即将截断液流从而液流形成对阀芯的反作用力。此外，从图中还可以看出改进的阀芯在6.50ms 之前，其所受到的瞬态液动力与原始阀芯受到的瞬态液动力基本相近；而在6.50ms 之后，改进的阀芯所受到的瞬态液动力明显要小于原始阀芯所受到的瞬态液动力。

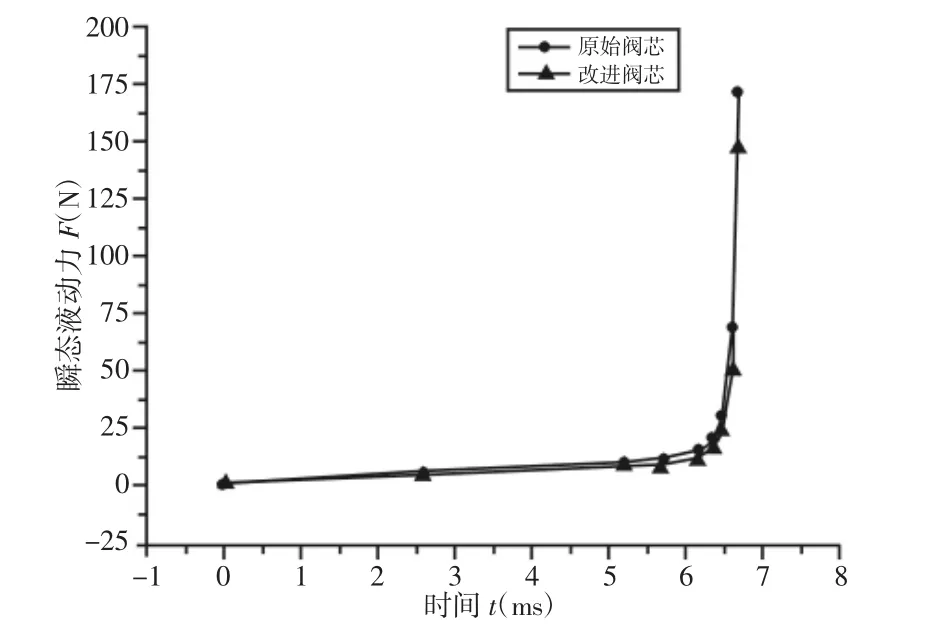
图7 两种阀芯结构下的瞬态液动力F/ΔL 曲线Fig.7 The Transient Hydrodynamic Force Curves of F/ΔL for Two Types of Valve Core

由上述分析再结合阀芯在插座内流场运动过程中所受到的弹簧力、液动力和粘性阻力；由于上述分析只考虑弹簧力在运动过程中的作用，但在实际运动过程中会有液动力和黏性阻力的作用，从而使得插座关闭时间有所延长。阀芯在关闭过程中的运动方程可由下式来控制[12]，即：

式中：m—阀芯以及与阀芯顶端相接触插头的质量；

Ft—弹簧作用在阀芯上的力；

Ff—黏性阻力；

Fp—流体对阀芯的液动力。

从上述分析可以推测，由于改进阀芯在插座关闭过程中所受到的液动力相对较小，而弹簧力相同且黏性阻力可以忽略，由式（11）可知，即改进后的阀芯加速度更大，即更容易在短时间内关闭插座，从而防止泄露。

6 结论

采用Fluent 动网格技术与UDF 相结合的方法对两种阀芯插座关闭过程中的内部流场和瞬态液动力进行探讨，同时对不同固定阀芯开度下的阻力水头损失和稳态液动力进行研究，可以得出如下结论：

（1）两种阀芯的hw均随阀芯开度ΔL 的减小而增加，当ΔL约为1.25mm 时，hw急剧上升，并且在此过程中改进阀芯的hw总是低于原始阀芯。

（2）两种阀芯在不同固定开度ΔL 下的稳态液动力均随ΔL的减小而增加，当ΔL 约为1.25mm 时，稳态液动力急剧上升，并且在此过程中的改进阀芯稳态液动力总是低于原始阀芯。

（3）在阀芯关闭过程中，两种阀芯的内部压力分布在开度ΔL 较大时基本一致，而开度ΔL 较小时改进阀芯的内部压力变化范围更小且更平稳。

（4）两种阀芯在关闭过程中所受到的瞬态液动力在6.50ms之前基本相近，而在6.50ms 之后改进阀芯所受到的瞬态液动力明显小于原始阀芯。

据上述结论可以推测，两种阀芯在实际运动过程中，改进后的阀芯所受到阻力小，更容易在短时间内关闭插座，从而有效地改善了阀芯延迟关闭的问题，进而减少介质的泄露。