基于数字图像技术的含双预制裂隙类岩石试样力学特性细观研究

李建旺

(1.北京科技大学金属矿山高效开采与安全教育部重点实验室，北京 100083；2.中铁十五局集团有限公司，上海 200070)

随着社会经济建设的持续发展，矿业工程、水利水电、土木工程等基础工程建设与资源开发正逐渐向深部岩层发展。而岩石作为一种重要的工程介质，由于受长期风化作用及人类活动影响，在其内部或表面产生了大量的裂纹和缺陷。而岩石力学特性与其内部预制裂隙的形状、大小、几何分布等因素密切相关。因此，深入开展含预制裂隙岩石破裂机制以及裂纹演化规律研究，对于地下岩石开挖工程的设计与施工，具有重要的研究意义。

在含预制裂隙岩石力学特性研究方面，近年来许多学者进行了大量的室内试验研究。潘鹏志等[1]采用EPCA2D对不同尺寸的非均质岩石试样进行单轴压缩破裂过程模拟，研究了不同加载条件对岩石宏观变形行为和破裂模式的影响；杨圣奇等[2-3]通过在真实砂岩中预制三条预制裂隙，分析了岩桥倾角对断续三预制裂隙砂岩试样强度的影响规律，探讨了单轴压缩下断续三预制裂隙砂岩试样的裂纹扩展机理；刘晓丽等[4]采用混合Mohr-Coulomb剪切破坏准则与拉应力破坏准则，分析了单轴压缩条件下含缺陷岩石的变形特性与强度，探讨了缺陷的演化规律及其对岩石宏观力学强度的影响；LI等[5]在单轴压缩试验条件下研究了预制裂隙大理岩试件裂纹的扩展及搭接。以上学者虽然对岩石中裂缝的扩展机制进行了一系列研究，但是其研究侧重于宏观方面，并未对裂纹扩展的细观及微观方面进行深入探讨。此外，随着计算机性能的大幅提高，RFPA、PFC等程序也被广泛用于含缺陷岩石宏细观力学特性及破裂机制的试验研究中。唐春安等[6]、朱万成等[7]采用RFPA程序开展了各类预制裂隙岩体力学特性及破裂机制研究。ZHANG等[8]采用颗粒流离散元软件PFC2D对单轴压缩条件下含单预制裂隙岩体裂纹的扩展过程进行了全真数值模拟；吴顺川等[9]、周喻等[10]采用颗粒流理论及PFC程序模拟了预制裂隙岩体中裂纹孕育、发展和贯通过程，揭示了岩样压缩过程中的破裂机理。以上学者通过颗粒流等软件对岩石中预制裂隙扩展的微观方面进行了研究，但因为是数值模拟，且岩石材料具有明显的非均匀性，仅从定性的角度还无法准确地表述裂纹

的扩展机制。

针对以上学者研究内容的不足，本文将通过构建含预制裂隙类岩石试样，采用DIC技术及PFC2D程序，探究单轴压缩条件下试样力学特性及裂纹孕育演化规律，重点揭示含预制裂隙岩样破裂时的细观机制，从定量的角度对裂纹的扩展作进一步的研究。

1 研究方法

1.1 试样制备

试样采用水泥砂浆搅拌混合而成，其中水泥、河沙和水的配比采用1∶2∶0.6。其中，水泥采用R42.5水泥，河沙采用粒径小于1.5 mm的天然细河沙。试验试样的尺寸为50 cm×50 cm×100 cm。试样内预制两条预制裂隙，均垂直并贯穿试样，与加载轴向方向的夹角为45°，两预制裂纹长10 cm，裂纹中心点距离试样形心水平方向距离20 cm，垂直距离10 cm，沿试样形心对称分布。预制裂纹的几何形态分布如图1(a)所示。浇筑后的水泥砂浆试样在室温条件下养护24 h后拆模，然后放入恒温(19.9 ℃)恒湿(97%)的养护箱内养护30 d。待试样制作成形后， 经清洗在其表面喷涂白色涂料， 待其干透后再随机涂洒黑色涂料，以形成随机散斑，如图1(b)所示。

图1 试样形态Fig.1 Illustration of specimen pattern

1.2 试验系统

试验系统由加载系统、观测系统及数据分析系统构成。加载系统采用YAW-600微机控制电液伺服岩石试验机。 加载方式采用位移控制，加载速率为0.002 mm/s。 当试样残余强度为峰值强度的20%时停止试验。观测系统包含一盏LED灯和一套数码拍摄装置。LED灯为试验提供稳定光源，以配合拍摄装置获得的图像具有稳定的灰度值。拍摄装置拍摄加载过程中试样表面裂纹的孕育演化过程。相机的快门速度为1/1 000 s，拍摄频率为60 张/s。

1.3 DIC技术

数字图像相关方法(DIC)又称数字散斑相关方法，是一种利用物体表面随机分布的斑点来给出变形场的非接触变形测量方法[11]。其基本思想是比较变形前后的物体图像的灰度值，识别其中的特定子区，进而获得物体的变形和应变。运用统计学比较变形前后同一区域图像灰度值的相关系数，通过多次计算相关系数可获取目标区域的位移场，基本原理如图2所示。以往的学者将数字图像技术应用到岩石裂纹扩展研究中，但是由于技术方面的限制，其研究成果始终不理想，理论与试验结果不相符。随着计算机技术的发展，DIC技术已被证实可以很好地应用于岩石裂纹扩展研究中。试验加载过程中同时采用数字图像技术(digital image correlation method，DIC)[11-13]，观测岩样裂纹的扩展规律， 该技

术由数据分析系统实现，采用的是美国Correlated Solutions公司的Vic-2D软件，将拍摄的全部照片导入Vic-2D软件，通过计算处理后就能得到试样破坏过程中应变和位移等相关图像数据。

图2 DIC基本原理图Fig.2 DIC basic schematic

1.4 数值模拟

为深入揭示含预制裂隙岩样的破裂机制，采用PFC2D程序[14-15]进行模拟。本文按实际试样尺寸建立0.5 m×0.5 m×1 m的计算模型，颗粒黏结选用平行黏结模型。为保证拟静力加载状态，本文将轴向加载速率设置为1.0，计算终止条件为：当试样残余强度达到峰值强度的20%时，停止计算。以裂纹的扩展、试样的应力-应变曲线和模拟试验曲线吻合作为PFC细观参数选取的准则。通过多次试算调整，使模拟与试验结果基本一致，最终确定的颗粒体模型及光滑节理模型细观力学参数见表1。

表1 颗粒体模型细观力学参数Table 1 Meso mechanical parameters of bonded particle model

2 试验与计算结果分析

2.1 预制裂隙对应力应变曲线的影响

1) 试验与数值计算对比。图3(a)和图3(b)分别为试验获取的试样应力-应变曲线，以及计算获取的试样应力-应变曲线、微破裂数。由应力-应变曲线可知，试验得到的试样峰值强度约为33.5 MPa，对应的应变约为5.1×10-3，其峰前弹性模量约为6.5 GPa；计算得到的试样峰值强度约为33.7 MPa，对应的应变约为5.1×10-3，其峰前弹性模量约为7.0 GPa。试验应力-应变曲线峰前阶段，在应变达到1.4×10-3之前，形成非线性变形，应力-应变曲线呈上凹型，此阶段为试样中原有孔隙压密阶段。之后直至达到峰值强度，应力-应变曲线呈近似线性上升趋势。达到峰值之后，应力-应变曲线伴随两次较大的应力降，一次应力降相对剧烈(应变从5.1×10-3到5.4×10-3)，一次应力降较缓和(应变从5.4×10-3到8.2×10-3)。计算应力-应变曲线峰前阶段从加载时起便近似呈线性上升趋势，这是由于构建的计算模型中颗粒均紧密接触，不存在颗粒接触数少于3的颗粒。峰值之后应力-应变曲线呈近似线性下降趋势。

2) 预制裂隙对破裂数的影响。计算中产生的微破裂数，是由于颗粒间承受的应力超过其黏结强度而发生破坏产生，可分为张拉型微破裂和剪切型微破裂。计算获取的微破裂总数为1 140次。其中，当应变达到5.1×10-3(即峰值)之前，微破裂较少，峰前微破裂总数为136，约占11.9%。在峰值强度之后，微破裂变得非常活跃，峰后微破裂总数为1 004次，约占88.1%。当应变为4.0×10-3、应力为27.5 MPa时，试样内部开始产生微破裂，即部分点已经破碎形成微小裂纹，但微裂纹的范围及密度不大。随后直至峰值时刻，微破裂频数呈迅速增加趋势。在峰值强度之后，微破裂产生更加活跃，伴随着剪切宏观裂纹的产生。总体而言，计算获取的试样应力-应变曲线特征，与试验结果较为一致。

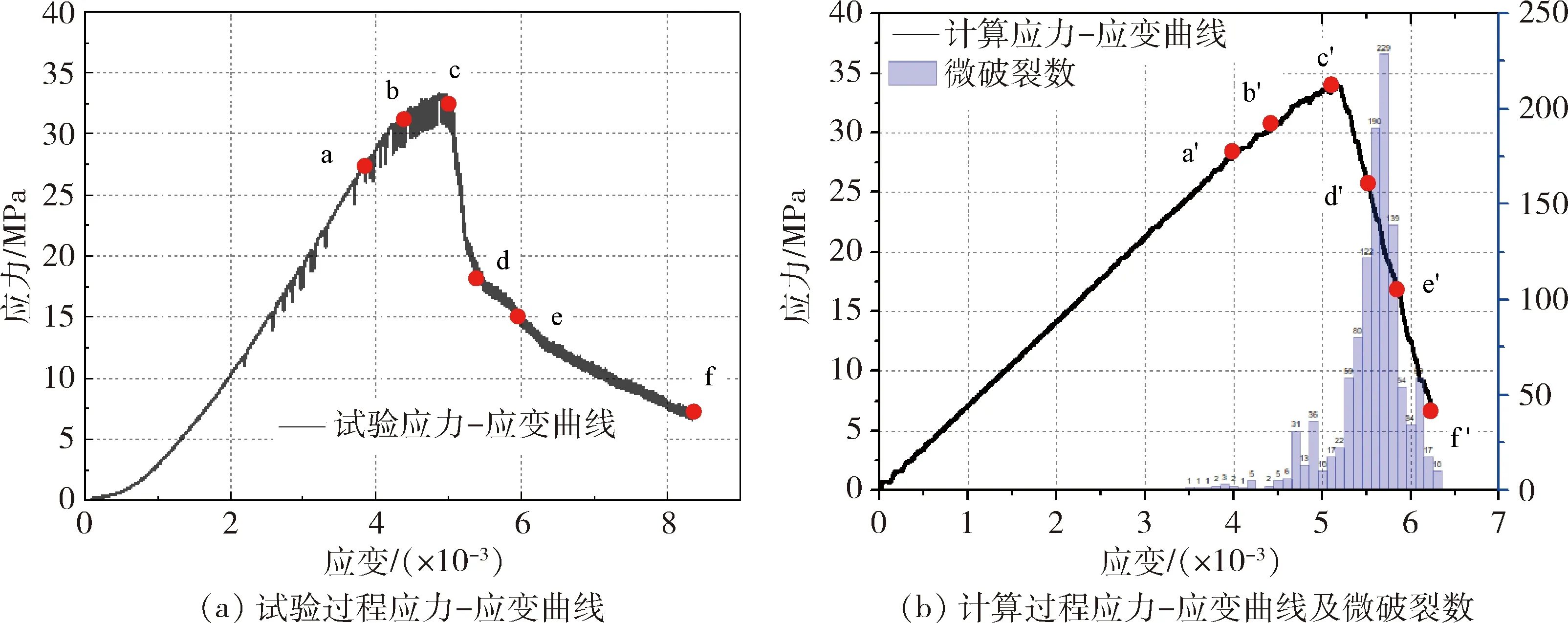
(a为试验过程中两条预制裂隙首先出现应力集中区域时刻；b为试验过程中预制裂隙A、B两个端部微破裂区逐渐增大时刻；c为试验过程中两条预制裂隙之间出现应力集中区域时刻；d为试验过程中两条预制裂隙两端的应力集中区域处于不稳定扩展阶段时刻；e为试验过程中A预制裂隙上端出现了应力集中区域时刻；f为试验结束时刻；a’为计算过程中微破裂首先在预制裂隙A、B两个端部产生时刻；b’为计算过程中微破裂逐渐增多时刻；c’为计算过程中预制裂隙A下端部产生并扩展裂纹时刻；d’为计算过程中预制裂隙A下端与预制裂隙B上端之间的Ⅱ型裂纹完全贯通时刻；e’为计算过程中预制裂隙A上端与试样边界的Ⅱ型裂纹完全贯通时刻；f’为计算结束时刻)图3 加载过程应力-应变曲线Fig.3 Loading stress-strain curve

2.2 预制裂隙对裂纹形成与分布的影响

在试样破坏过程中产生的宏观裂纹可分为两类：一类是Ⅰ型裂纹(也可称为翼形张拉裂纹)，其宽度通常相对纤细并沿加载方向发展；另一类是Ⅱ型裂纹(也可称为剪切裂纹)，其宽度通常较宽，并沿着与加载方向成一定角度发展。图4为试验过程中不同时期的全场应变云图，图4中的云图对应埃尔-拉格朗日系数，此系数正比于试件所受到的应变，即数值越大，说明应变越大，其对应的应力应变状态已在图3(a)标注。

1) 载荷对破裂区的影响。可以发现：当试验应力-应变曲线达到a点时，即应变为3.9×10-3、应力为27.0 MPa，发现两条预制裂隙A、B两个端部首先出现应力集中区域，这说明了应力首先集中于预制裂隙尖端，这是Ⅰ型裂纹出现的结果，此时可以观察到微破裂区的形状为椭圆形，与预制裂隙端部相连。

随着载荷继续增加，当试验应力-应变曲线达到b点时，即应变为4.4×10-3、应力为31.0 MPa，与状态云图4(a)相比，预制裂隙A、B两个端部微破裂区逐渐增大，且预制裂隙尖端出现更高的应力集中区域，这说明了微破裂区的范围在增大，但微裂纹的范围及密度不大，尚未成核导致宏观裂纹。当应力达到峰值强度时刻c点，即应变为5.1×10-3、应力为33.5 MPa，两条预制裂隙之间出现应力集中区域，此时产生的是Ⅱ型裂纹，观察微破裂区发现初始裂纹和新生裂纹周围也会产生应力集中区域，说明Ⅰ型裂纹处于迅速扩展阶段。当试验应力达到峰后的d点时，即应变为5.4×10-3、应力为17.5 MPa，两条预制裂隙两端的应力集中区域处于不稳定扩展阶段，预制裂隙之间的应力集中区域逐渐增大，并且预制裂隙两端的应力集中区域相连，预制裂隙两端之间的Ⅱ型裂纹贯通，说明两条预制裂隙两个端的岩桥已经贯通，观察微破裂区的扩展路径发现它逐渐弯曲，并不断向最大压应力方向靠近。当试验应力-应变曲线达到e点时，即应变为6.0×10-3、应力为15.0 MPa，此时已发生过一次明显的应力下降，在上方预制裂隙上端出现了应力集中区域，说明Ⅱ型裂纹在快速扩展。当试验应力-应变曲线达到f点时，即应变为8.2×10-3、应力为6.7 MPa，即试验结束时刻，此时预制裂隙A上端的Ⅱ型裂纹进一步扩展，而预制裂隙B下侧亦产生了Ⅱ型裂纹并最终贯通整个试样，而在预制裂隙外侧Ⅱ型裂纹扩展过程中，只有少量的Ⅰ型裂纹从中孕育演化。

2) 破裂区演化过程。图5为计算获取的微破裂孕育演化过程，其对应的应力应变状态已在图3(b)标注。在峰值强度之前，当试验应力-应变曲线达到a′点时，即应变为应变为4.0×10-3、应力为28.0 MPa，微破裂首先在预制裂隙A、B两个端部产生，并形成初始的Ⅰ型裂纹。

当试验应力-应变曲线达到b′点时，即应变为4.4×10-3、应力为31.0 MPa，预制裂隙A、B两个端部的Ⅰ型裂纹进一步扩展，微破裂逐渐增多。应力达到峰值c′点时，即应变为5.1×10-3、应力为33.7 MPa，构成Ⅱ型裂纹的微破裂开始在预制裂隙A下端部产生并扩展，预制裂隙A、B上下端的Ⅰ型裂纹亦进一步扩展。在峰值强度之后，当试验应力-应变曲线达到d′点时，即当应变为5.5×10-3、应力为26.0 MPa时，预制裂隙A下端与预制裂隙B上端之间的Ⅱ型裂纹完全贯通，此时两条预制裂隙两个端的岩桥已经贯通。当试验应力-应变曲线达到e′点时，即应变为5.9×10-3、应力为17.0 MPa时，此时已发生过一次幅度值较大的应力降，预制裂隙A上端与试样边界的Ⅱ型裂纹完全贯通。当试验应力-应变曲线达到f′点时，即应变为6.4×10-3、应力为6.8 MPa时，预制裂隙B下端与试样边界间的Ⅱ型裂纹也完全贯通。在峰值之后，可以通过图片变化观测到在Ⅱ型裂纹扩展过程中，亦有少量的Ⅰ型裂纹从中孕育演化。总体上讲，试验各个阶段与数值模拟各个阶段裂纹演化的特征较为一致。

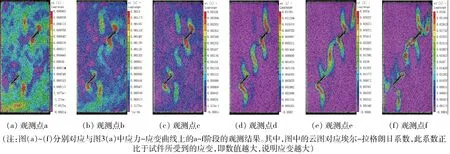
图4 试验全场应变云图Fig.4 Experimental full-field strain contour maps

图5 计算过程中微破裂孕育演化Fig.5 Evolution of micro-inasion in calculated process

2.3 预制裂隙对位移场(U，V)演化的影响

1) 预制裂隙对X位移场的影响。图6为试验过程中不同时期的X方向(垂直载荷方向)的全场位移云图，其对应的应力应变状态已在图3(a)中标注。图6和图7的数值单位均为像素，此像素表现为云图，根据此云图可分析特定区域的变形状态，此像素值正比于位移值，像素越大即是位移越大。根据图像的变化，可以发现：在两条预制裂隙的右边位移为正值，左边为负值。说明了在预制裂隙左侧，试样表面向左剥离，预制裂隙右侧，试样表面向右剥离，并随着载荷的增大，全场位移绝对值逐渐增大。在应力达到峰值强度之前，即应变为5.1×10-3、应力为33.5 MPa，位移量的增大并不明显，之后，在裂纹的扩展阶段，位移量迅速增加。在脆性破坏后，右边位移量达到最大的0.268 mm，而在试验结束时，左边位移量达到最大的0.91 mm。

2) 预制裂隙对Y位移场的影响。图7为试验过程中不同时期的Y方向(平行载荷方向)的全场位移云图，其对应的应力应变状态已在图3(a)中标注。根据图像的变化，可以发现：每条预制裂隙下方的位移量比上方的位移量大，且位移量从固定端(下端)向加载端由大到小呈梯度分布。 在应变为6.0×10-3、应力为15.0 MPa之前，随载荷的增大，全场位移值逐渐增大，直接反映出试样表面受力后沿平行载荷方向压缩。当应变为8.2×10-3、应力为6.7 MPa时，即试验结束时刻，平行载荷方向位移出现明显的变化，位移量全变为负值，并沿载荷方向呈条形分布。

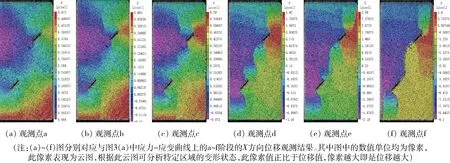
图6 X方向的全场位移云图Fig.6 Full-field displacement contours in direction X

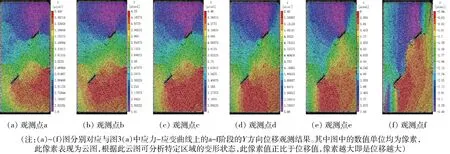
图7 Y方向的全场位移云图Fig.7 Full-field displacement contours in direction Y

3 结 论

1) 当载荷到达一定阶段，预制裂隙两端首先出现明显的微破裂区，其形状近似椭圆，开始形成宏观Ⅰ型裂纹(翼形张拉裂纹)。

2) 随着载荷的增大，微破裂聚集，预制裂隙端部开始形成宏观Ⅱ型裂纹(剪切裂纹)，并与Ⅰ型裂纹一起持续发育直至试样破坏。

3) 预制裂隙左右两侧和上下两侧的X方向和Y方向位移量差别很大，X方向位移量在两条预制裂隙的右边位移为正值，左边为负值；Y方向位移量自固定端(下端)向加载端呈由大到小呈梯度分布。

4) 将数字图像技术与常规加载试验相结合，能有效反映试样内部裂纹的产生以及扩展规律，并结合PFC模拟分析比较，验证了该试验方法的准确性。

综上所述，本文针对特定方向的预制裂隙对岩石试件裂纹扩展的细观机理做了相关的研究，弥补了现有研究中定量表述裂纹扩展方面内容的缺失，但是因实际情况复杂多变，其裂缝也是纵横交错，无法和实验室中如此规整的裂缝相提并论，后续还需研究多方向、多尺寸的裂缝在荷载作用下其裂纹扩展的细观机理。