运用加权马尔科夫模型预测我国PMI
舒服华
(武汉理工大学 继续教育学院,武汉 430070)
PMI(采购经理人指数),是反映制造业在生产、新订单、商品价格、存货、雇员、订单交货、新出口订单和进口八个方面状况的指数,是考察一个国家制造业的“体检表”。PMI大于50,表明经济处于扩张状态;小于50,则预示经济处于衰退状态;低于40时,表明经济处于萧条阶段。PMI与社会消费关系最为密切,PMI低,反映生产商采购减少,社会总需求下降,消费不振,经济增长乏力。PMI与GDP也有着紧密的关系,PMI低,反映生产者的投资和生产活动不活跃,社会产出减少,GDP或GDP增速会随之下降,但有一定的滞后期。PMI与物价水平也有关系,PMI低,反映社会采购量减少,需求不旺,导致市场供过于求,必然引起物价下降。PMI与老百姓的生活也不无关系,PMI低,表明企业开工缩减,用工量减少,导致失业率上升,民众的整体收入下降,生活水平降低。总之,PMI不仅是一个经济问题,也是一个社会问题;不仅反映经济的景气度,也反映民众的幸福感。保持PMI扩张态势,是维护经济社会稳定的关键。科学预测PMI的变化趋势,对监测国民经济运行状况,据此制定宏观经济调控政策、指导企业进行合理的生产经营活动、促进经济健康发展都具有重要的意义。我国学者对PMI与其他经济指标的关系进行了研究,比如,丁勇等研究了PMI与宏观经济之间的关系[1];丁黎黎等研究了PMI对GDP的影响[2];李娜研究了PMI对出口订单的影响[3];李跃等研究了PMI,CPI,CSI之间的关系[4];盛煌等研究了PMI与上证指数的关系[5];赵怡研究了CPI,PPI,PMI之间的关系[6]。我国学者对PMI预测也有少量研究,如王檬运用自回归滑动平均模型对我国制造业PMI进行了预测[7];舒服华等运用向量自回归模型对我国PMI和PPI进行了预测[8]。
虽然PMI受政治、内外经济环境、社会环境甚至生态环境等诸多因素的影响,但近几年,我国政局稳定,经济社会发展有序,PMI没有大起大落,波动幅度不大。因此,我国PMI大体可以看作是一个随机的时间序列,那么,通过挖掘其内部隐含的信息能够推断PMI的基本发展走势。马尔科夫预测模型可以通过对大量历史资料的统计分析,推断事物的未来走势,在许多领域得到了广泛的应用[9-14]。但传统的马尔科夫预测模型不仅忽视了不同时期的历史数据对判断事物后期发展影响程度的不同,而且只能对事物的发展趋势作定性分析。本研究通过对历史数据进行加权和借鉴模糊数学处理预测结果的方法,对传统马尔科夫预测模型进行改进,使其能客观反映不同时期的历史数据对预测结果的影响,并能对预测对象进行定量描述,然后运用改进后的马尔科夫预测模型对我国PMI走势进行预测。
1 加权马尔科夫预测模型
马尔科夫过程是研究事物状态及状态转移规律的统计特性理论,它通过不同状态的初始概率及状态的转移概率来确定状态之间的变化趋势,以达到预测事物未来发展状况的目的。马尔科夫过程最基本的特征是无后效性。马尔科夫理论认为,事物的“将来”状态只与“现在”的状态有关,与“过去”的状态无关,即系统变量t+s时刻的一个状态值只与t时刻的状态相关,而与t时刻以前的状态无关。马尔科夫预测模型的基本原理是:依据变量的前若干时段的状态值,对变量的后某一时段的状态进行预测。传统的马尔科夫预测模型只能用作变量的定性预测,并且将变量之前各时刻的状态值对后续目标预测的影响均衡对待,没有考虑变量不同时刻的状态值对预测后面状态值的作用不同,应用范围受到了一定的限制,预测精度也不尽如人意。
本研究采用改进的加权马尔科夫预测模型预测变量发展趋势,其一,对变量在不同时刻的数据依据其特点采用不同的权重,合理利用全部已知信息;其二,运用模糊数学中的级别特征值法定量计算预测目标的具体值,以提高方法的适用性。加权马尔科夫预测方法具体步骤如下。
1.1 变量状态级别划分
一般根据变量xi的已知样本均值μ和标准差σ将变量状态值划分为若干级别。本研究将我国PMI状态划分为5个级别,具体如表1所示。

表1 变量状态级别划分标准
1.2 求1步(基准时刻)和n步状态转移概率矩阵
1步状态转移概率矩阵P1={pij},其中:
(1)
式中,sij为数据样本中状态Si经过1步转移到状态Sj的次数,∑si表示状态Si在样本中出现的总次数。
n步状态转移概率矩阵为:
Pn=P1n。
(2)
1.3 计算各阶的自相关系数
阶数是为预测系统变量而选取的状态转移的步数,一般取4-6,各阶的自相关系数为:
(3)
式中,rk为第k阶的自相关系数,n为系统变量的样本长度。
1.4 计算各阶的权重
所选取系统变量各时段值(各阶)的权重为:
(4)
式中,m为预测时需要计算的最大阶数。
1.5 构建预测状态转移概率矩阵
根据求出的不同步长的状态转移概率矩阵和滞后期,以第一个选定的基本时刻为初始状态,结合各阶的状态转移概率矩阵以及滞后时刻的状态,构建预测状态转移概率矩阵。
P={pi(k)},
(5)
式中,k为步长;pi(k)为状况Si第k阶的概率值(即预测状态转移概率矩阵中第k行第i列的概率值)。
1.6 计算预测变量各状态的概率
预测变量各状态的概率为其在预测状态转移概率矩阵中各阶状况转移概率与对应的权重之积的和,即:
(6)
状态转移概率最大的状态即为预测目标对应的预测状态。
1.7 求级别特征值
首先计算各阶的模糊数:
(7)
式中,di为各阶对应的模糊数;η为最大概率作用指数,其值越大,越能突出最大概率的作用,一般η=0.5~1.0,于是,级别特征值为:
(8)
1.8 求变量的预测值
变量在t+s时刻的预测值为:
(9)
式中,Ti和Bi分别为状态Si的上、下限,i为状态级别。
2 我国PMI走势预测
图1为2015年1月-2019年3月我国PMI走势图(数据来源于国家统计局)。从图1可知,在这51个月内我国PMI基本稳定,最小为49.0,最大为52.4,均在50的分界线附近,略呈上升势头,说明三年多来我国经济运行状态基本上是好的。
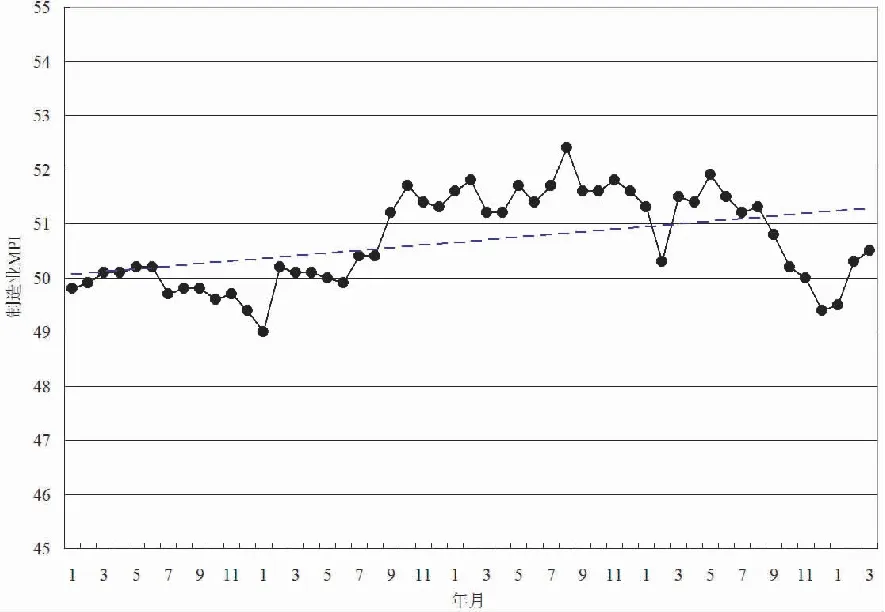
图1 2015年1月-2019年3月我国PMI走势图
以我国这51个月PMI统计资料为基础,利用加权马尔科夫模型预测我国2019年4月的PMI。通过计算,在这51个月中,PMI的平均值μ=50.68,标准差σ=0.853,根据表1中的PMI状态划分方法,将PMI状态划分为S1,S2,S3,S4,S5,它们的界定范围如下:S1∈(-∞,49.827);S2∈[49.827,50.254);S3∈[50.254,51.107);S4∈[51.107,51.534);S5∈[51.534,+∞)。则这51个月PMI状态级别划分结果如表2所示。

表2 2015年1月-2019年3月我国PMI状态级别划分
取步长为5,即时滞为5个月,计算1-5步的转移概率。
以1步状态转移概率为例:状态转移概率矩阵每行代表一个对应的状态,p11也就是一步状态转移概率矩阵中第1行第1列的概率值。p11=s11(1)/s1,s11(1)表示样本中状态S1经过1步转移到状态S1的次数,s1表示状态S1在样本中出现的次数,当S1出现在数据序列的最后一位时,则不计入s1中。
从表2知,S1经过1步转移到状态S1的次数共有7次,分别为2015年7月到8月、8月到9月、9月到10月、10月到11月、11月到12月、2015年12月到2016年1月以及2018年12月到2019年1月,S1在样本中共出现10次,且未出现在最后一位,故p11=7/10;S1经过1步转移到状态S2的次数为2次,分别为2015年1月到2月和2016年1月到2月,故p12=2/10=1/5;S1经过1步转移到状态S3的次数有1次,即2019年1月到2月,故p13=1/10;S1经过1步转移到状态S4的次数为0,故p14=0;S1经过1步转移到状态S5的次数为0,故p15=0。同理,可求得1步转移概率矩阵P1中其他行元素的值,根据计算的状态转移pij,可得到1步转移概率矩阵:
根据求1步转移概率矩阵P1方法,可分别得到2步、3步、4步、5步转移概率矩阵,依次如下:

对模型进行显著性检验。显著检验的目的是检验变量序列是否满足马尔科夫模型的应用条件,即样本数据序列是否呈卡方分布。如果统计量χ2>χ20.05(m-1),则变量序列适合用马尔科夫模型进行处理。经计算χ2=31.724,而χ20.05(4)=26.296,χ2>χ20.05(m-1),因此,2015年1月至2019年3月我国PMI满足马尔科夫性,适用于马尔科夫预测模型。
马尔科夫预测模型满足无偏性,虽然一般不满足一致性,但如果样本足够大,并且样本数据波动不大,是基本可以满足一致性的。本研究选取了51个样本,样本数量较大,而这51个月的PMI最小为49,最大为52.4,波动幅度为6.49%,样本数据波动较小,可认为满足一致性要求,适用于马尔科夫预测模型。
求各阶的自相关系数,即k=5,由式(3)求得各阶的自相关系数为:r1=0.841,r2=0.741,r3=0.673,r4=0.584,r5=0.518。
根据各阶自相关系数由式(4)求得其权重为:w1=0.251,w2=0.221,w3=0.201,w4=0.174,w5=0.154。
用2019年3月的PMI数据来检验模型的性能,然后用模型预测2019年4月的PMI。由于滞后期为5阶,则根据2018年10月-2019年2月的PMI所处的状态,构建相应的预测状态转移概率矩阵,预测2019年3月的PMI。因为2018年10月的PMI处于状态S2,故取P1的第2行作为预测状态转移概率矩阵的第1行;2018年11月的PMI处于状态S2,取P2的第2行作为预测状态转移概率矩阵的第2行;2018年12月的PMI处于状S1,取P3的第1行作为预测状态转移概率矩阵的第3行;2019年1月的PMI处于状态S1,取P4的第1行作为预测状态转移概率矩阵的第4行;2019年2月的PMI处于状态S3,取P5的第3行作为预测状态转移概率矩阵的第5行。构建的预测概率矩阵(矩阵的表格形式)如表3所示。

表3 2019年3月PMI预测概率矩阵
先将权重乘预测状态转移概率矩阵对应的各行元素数据,然后将预测状态转移概率矩阵各列元素数据相加,得到各状态最终状态转移概率值。从表3可知,状态S2的转移概率0.511在所有状态转移概率中最大,故预测2019年3月的PMI处于状态S2。
根据预测概率矩阵,求2019年3月的PMI。首先计算状态级别特征值,由各状态最终状态转移概率值,求其模糊数di。取η=0.50,由式(7)-(8)预测目标各状态的模糊数为:
d1=0.234,d2=0.298,d3=0.252,d4=0.122,d5=0.092。
于是,可求得状况级别的特征值为:
H=0.234×1+0.298×2+0.252×3+0.122×4+0.092×5=2.534。
由于H=2.534>i=2,于是求得2019年3月的PMI预测值为:
x2019/3=(2.534×49.827)/(2+0.5)=50.505。
而2019年3月的实际PMI为50.5则模型的预测误差为:
ε=100×(50.505-50.5)/50.5=0.01%。
预测误差很小,说明模型具有较高的预测精度,模型是有效和可靠的,可用于预测我国PMI的走势。
下面预测2019年4月的PMI。依照上述方法构建2019年4月的PMI预测概率矩阵,计算各最终状态转移概率值,结果如表4所示。从表4可知,状态S2的转移概率0.408在所有状态转移概率中最大,故预测2019年4月的PMI处于状态S2。

表4 2019年4月PMI预测概率矩阵
同理,取η=0.5,求得预测目标各状态的模糊数为:
d1=0.271,d2=0.313,d3=0.155,d4=0.140,d5=0.121。
于是,求得状况级别的特征值为:H=2.527。
由于H=2.527>i=2,所以由式(9)求得2019年4月的PMI预测值为:
x2019/4=(49.827×2.527)/(2+0.5)=50.365。
马尔科夫预测虽然可对随机时间序列的发展趋势进行预测,但只能作短期预测,也就是预测样本数据外延后一期的值,不能作长期预测,若要进行长期预测,则需要结合灰色模型、神经网络模型等。
3 结语
要实现到本世纪中叶把我国建设成社会主义现代化强国的宏伟目标,根本的途径是发展经济,即在相当长的一段时间内,我国经济必须保持一定的增长速度,也就是要求PMI向扩张性方向行进。但近些年,由于受国际经济不确定因素的影响,我国制造业PMI长期在50的临界线上下徘徊,经济下行压力不断加大,给我国经济的长久发展带来了严重的挑战。要克服当前我国经济发展中遇到的困难,必须深化经济体制改革,创新经济发展模式。
第一,转变经济发展方式。过去,我国经济主要依靠投资和出口拉动,长期的高投资,不仅使我国的自然资源严重透支,生态环境遭到不同程度的破坏,而且低水平重复建设导致一些行业产能严重过剩,企业经济效益下滑,造成资源浪费,投资效应也在逐步减弱。同时,目前国际贸易摩擦不断,保护主义、单边主义日益抬头,我国出口经济受到挫折,出口对经济的拉动作用也在减弱,使得我国的PMI波动震荡,难以大步向前。面对这样的国内国际经济形势,必须加快转变我国经济的发展方式,坚持内涵式发展,优化调整产业结构,淘汰落后产能,积极扩大内需,让消费成为驱动经济发展的新动力,促进生产经营活动趋旺,带动我国PMI上扬。
第二,推进产业升级,提高我国在国际分工中的地位。我国虽然是制造大国,但长期处于国际分工的低端,利润低,市场竞争激烈,难以支撑我国经济长期稳定增长,这也是我国PMI疲软的一个重要原因。必须大力推进产业结构优化升级,发展战略性新兴产业,促进国民经济战略性调整,逐步使我国产业从产业链低端迈向产业链中高端,从价值链低端迈向价值链高端,提高中国制造的技术含量、产品的附加值,提高劳动生产率,提高企业的经济效益,提高我国产品在国际市场上的竞争力,推动我国制造业高质量发展。
第三,加强科技创新。目前,我国大部分行业的技术水平还处于跟跑阶段,一些核心技术受制于人,不仅限制了我国经济的高质量发展,也成为制约我国经济进一步发展的瓶颈。许多发明专利被外国公司垄断,使得许多企业每年都要付出大量的专利费,企业的利润变薄,导致一些产品市场占有率上升、利润反而下降的尴尬局面。PMI虽然有时也走强,但不能有效创造社会财富,带来效益。核心技术是买不来、要不来、讨不来的,必须加强自主创新能力,使我国尽早产生一大批具有自主知识产权的原创性新技术,加快科技成果转换,让更多的先进技术转换为现实生产力,以创新引领发展,使我国从制造大国迈向制造强国,用不断的科技创新支撑我国经济的持久发展,让PMI更有实效、更有质量、更有温度。
研究PMI变化发展的趋势,对分析经济与商业活动中出现的问题和情况,制定宏观经济调控方案,指导企业的采购、生产、经营等活动具有重要的作用。由于传统马尔科夫预测模型对历史数据均等对待,限制了有价值信息作用的发挥,且对预测目标只能作粗略估计,所以本研究采用对不同时期的历史数据设置权重的方法对其进行改进,强调了有价值信息的功用,充分利用了原始信息,同时运用模糊数学的方法处理预测结果,使预测结果更加具体细致。运用加权马尔科夫预测模型对我国PMI进行预测,得到2019年4月我国PMI为50.365。

