基于机器学习的公平数据交易*

赵艳琦, 于 斌, 李慧琳, 陈若楠, 禹 勇

1. 陕西师范大学 计算机科学学院, 西安710119

2. 密码科学技术国家重点实验室, 北京100878

3. 西安电子科技大学 计算机科学与技术学院, 西安710071

1 引言

随着物联网和5G 技术的蓬勃发展, 智能家居、智慧城市、智能工厂等新兴服务及业务不断涌现[1].全球物联网设备(智能手机、传感器设备、智能家电) 数量持续增长, 据IDC 预测, 到2025 年将有386亿台物联网设备接入互联网, 至2030 年, 这一数字将超过500 亿台[2]. 物联网设备应用的同时也产生了海量的用户数据. 各大企业包括Facebook、阿里巴巴、IBM、腾讯等正在积极研发相关产品, 收集和处理用户数据, 并利用机器学习和数据挖掘等先进技术进行大数据分析, 做出市场决策, 改善产品服务质量[3].海量数据已然成为无价的资产, 并由此催生出一种新兴的数据交易模式: 数据市场, 如DataExchange[4],数据持有者可以通过分享数据来获得经济回报. 已有的数据市场, 数据持有者首先封装数据, 并将数据集提交给数据市场, 当数据消费者向数据市场提交自身需求时, 数据市场将该需求与数据集进行匹配. 之后,数据持有者与数据消费者交互完成数据交易. 数据市场作为中心化可信第三方, 参与整个数据交易流, 将消费者需求进行匹配, 数据市场将收取昂贵的手续费, 同时中心化数据市场可能存在服务器宕机, 单点失败的问题. 如何构建去中心化数据交易, 实现数据持有者与数据消费者的交易公平, 成为亟待解决的问题.

区块链是一种基于Hash 的分布式数据结构, 结合Peer-to-Peer 网络、密码算法、共识机制构成了比特币货币系统[5], 在区块链网络中矿工根据共识算法生成新的区块, 新的区块包含指向前一个区块的哈希指针和交易单, 其具有去中心化、防篡改、可公开验证、可公开审计等特性, 引起了学术界及工业界的广泛关注[6,7]. 区块链的出现为实现去中心化的数据交易提供了一种可能. 然而, 要实现数据持有者与数据消费者公平数据交易, 还需解决如下挑战: (1) 数据持有者数据的可靠性. (2) 数据持有者与数据消费者之间原子交换的公平性.

相关工作: Delgado-Segura 等[8]提出基于比特币交易单的公平数据交易协议, 采用操作码OP_AND 构建交易单完成公平付费, 但在比特币交易单中这一操作码是禁止使用的, 使得方案不能实际部署.Zhou 等[9]结合区块链技术提出基于区块链的分布式数据售卖框架, 其结合数据嵌入和距离度量学习构建数据索引, 实现数据检索和隐私保护之间的折中. Chen 等[10]提出基于区块链的大数据交换生态系统, 采用区块链作为分布式数据库, 记录事务日志和其他重要文档. Goldfeder 等[11]借助托管服务用于购买实体商品, 结合比特币系统及门限密码学提出一系列解决方案, 保证购买实体商品的安全性和隐私性.2014 年, Andrychowicz 等[12]提出基于比特币的安全多方计算方案, 采用交押金的方式实现多用户的公平博彩. 比特币核心开发者Gregory Maxwell, 通过比特币网络部署零知识有条件付费(Zero Knowledge Contingent Payment, ZKCP)[13,14]实现了首个数独付费(Pay-to-Sudoku) 协议. 同年, Banasik 等[15]提出不采用脚本语言的有效零知识有条件付费(Efficient Zero Knowledge Contingent Payment) 协议,以期改进方案的实用性. 2017 年, Tramèr 等[16]给出ZKCP 在以太坊[17]上的执行方式. Campanelli等[18]提出零知识有条件服务付费(Zero Knowledge Contingent Service Payment, ZKCSP) 协议, 应用ZKCSP 解决外包存储付费问题. 田等[19,20]基于传统的可验证加密签名和盲签名, 构造盲的可验证加密签名体制, 借助比特币交易单实现公平合同签署. 高等[21]结合可验证加密签名和聚合签名, 提出无证书的聚合可验证加密签名方案, 利用该方案设计出基于区块链的多方合同签署协议. Dziembowski, Eckey和Faust 给出基于UC 框架的公平交换模型[22], 采用Proof-of-Misbehavior (POM) 方法, 避免采用复杂的零知识证明. 为解决数据市场中数据交易问题, Zhao 等[23]结合以太坊提出基于机器学习的公平交易协议, 协议通过市场管理员处理争议. Fuchsbauer[24]指出文献[18] 的解决方案不能保证有条件付费的公平性, 其采用证据不可区分安全强度不够, 并提出新的有条件付费解决方法. Hu 等[25]提出zkPoD 实用的数据交换去中心化系统, 借助Pederson 承诺, 给出三种交换模型以期实现数据交换的实用性, 但系统初始化仍需要可信第三方参与. 表1 给出与各方案的技术对比。借助区块链技术实现公平交换的机制受到一定程度的关注, 但已有机制不足以确保公平数据交易的公平性和交易数据的可靠性.

方案 去中心化 挑战-响应 匿名性 主要技术Dziembowski et al. [22]√ --PoM Zhao et al. [23] - √ √ 确定性加密Fuchsbauer et al. [24]√--ZK-SNARKs Hu et al. [25] - √ - Pederson 承诺本文 √ √ - 向量承诺

本文提出一种基于机器学习的公平数据交易协议, 满足数据交易的可靠性和公平性. 协议采用区块链架构, 借以消除单点失败(Single Point of Failure) 问题. 运用向量承诺和反向传播(Back Propagation)神经网络, 使得数据消费者可对数据进行有效抽样, 验证数据的可靠性, 并结合智能合约实现原子交换的公平性. 协议适用于异步网络, 智能合约无需设置时间断点, 由数据持有者或数据消费者自行触发, 因此,协议使得恶意的数据持有者或数据消费者达到公平. 最后, 通过部署智能合约, 验证基于机器学习的公平数据交易协议的实用性.

本文针对数据交易的公平性和可靠性展开研究. 第2 节介绍相关的预备知识. 第3 节介绍基于机器学习的公平数据交易模型. 第4 节给出具体的基于机器学习的公平数据交易协议, 安全性及性能分析. 第5 节给出总结.

2 预备知识

2.1 智能合约

智能合约[26]最早由Nike Szabo 提出, 是一种可自动执行的程序代码. 在区块链网络中, 可以部署智能合约, 创建更富表现力的应用. 比特币脚本语言支持简单的智能合约, 但这种脚本语言是基于堆栈的编程语言, 非图灵完备的. 以太坊作为区块链平台, 支持更复杂的智能合约, 用于构建下一代分布式应用[27].

2.2 BP 神经网络

机器学习通过从数据中生成的模型来学习如何执行某些特定任务. 根据训练数据是否包含标记可分为两类学习任务, 即监督学习和无监督学习. 监督学习主要为分类和回归, 无监督学习主要为聚类. 如果想要预测的结果是一些离散值, 则这种学习任务称为分类. 如果结果是连续值, 则学习任务称为回归. 而聚类是将训练集中的样本数据分为几类的学习任务, 并且训练样本通常不含标记. 作为一种功能强大的数据建模工具, 人工神经网络(Artificial Neural Network, ANN) 能够从示例中捕获并表示复杂的输入/输出关系, 而无需假设数据分布或输入与输出之间关系的性质. 从理论上讲, 作为典型ANN 之一的BP 神经网络可以近似任何非线性函数. 它消除了传统回归方法的局限性, 并准确地建立了输入和输出变量之间的映射. BP 神经网络能够以更高的精度逼近任意非线性函数. 本文采用BP 神经网络[28]以获得的明文中的单词为输入, 对文本数据进行分类.

2.3 向量承诺

向量承诺最早由Catalano 和Fiore 提出[29], 在可验证数据库更新及零知识数据库更新[29]中广泛应用. 向量承诺可以有效承诺消息序列(m1,··· ,mq), 支持在特定位置打开承诺, 对于同一位置不能打开两个不同值, 即满足位置绑定性. 向量承诺支持有效更新, 将对应打开消息进行更新, 生成新的承诺值. 向量承诺应满足简洁性, 即承诺和打开的字符串长度应与消息序列长度无关. 向量承诺形式化定义[29]如下:

定义1 向量承诺方案由以下六个算法定义:

(1) 密钥生成算法VC.Keygen: 输入安全参数k 以及承诺向量的大小q, 输出公开参数parameters,记为(parameters)←VC.Keygen(1k,q).

(2) 承诺算法VC.Com: 输入消息序列(m1,··· ,mq) 和公开参数parameters, 输出承诺值C 和辅助信息aux, 记为(C,aux)←VC.Com((m1,··· ,mq),parameters).

(3) 打开算法VC.Open: 输入第i 位的消息mi以及辅助信息aux, 输出对应消息的证明Λi, 记为(Λi)←VC.Open(i,mi,aux).

(4) 验证算法VC.Ver: 输入承诺值C, 第i 位的消息mi以及证明Λi, 验证Λi是否为mi的有效证明, 有效记为VC.Ver(C,i,mi,Λi)=1, 无效记为VC.Ver(C,i,mi,Λi)=0.

(5) 更新算法VC.Update: 输入承诺值C, 第i 位的旧消息mi以及新消息m′i, 输出新的承诺值C′和更新信息U, 记为(C′,U)←VC.Update(C,i,mi,m′i).

(6) 证明更新算法VC.Proofupdate: 输入承诺值C, 更新信息U, 第i 位的消息m′i, 证明Λj对应第j 位, 输出对应的承诺值C′的证明Λ′j, 记为(Λ′j)←VC.Proofupdate(C,U,i,m′i,Λj).

3 基于机器学习的公平数据交易模型

如图1 所示, 数据交易主要包含3 个实体, 分别为数据持有者, 数据消费者, 区块链. 数据持有者与数据消费者进行数据的售卖与交换并维护区块链.

图1 基于机器学习的公平数据交易模型Figure 1 Model of based on machine learning data trading

数据持有者: 数据持有者作为数据收集者和生产者, 生成数据索引列表, 与数据消费者进行交互, 执行数据交易, 触发智能合约获取付费.

数据消费者: 数据消费者作为数据的购买方, 验证数据持有者数据的可靠性, 与数据持有者进行交互,部署智能合约, 对满足需要的数据进行付费.

区块链: 记录数据交易公开参数, 维护数据持有者与数据消费者上传的交易单, 执行智能合约.

定义2 基于机器学习的公平数据交易协议

该协议由以下6 个算法组成:

(1) 初始化算法Setup: 输入安全参数k, 输出公开参数pp, 记为(pp)←Setup(1k).

(2) 密钥生成算法Keygen: 数据持有者运行VC.Keygen 算法(parameters) ←VC.Keygen(1k,q)生成公开参数parameters. 输入pp 和parameters, 输出pk = (parameters), sk = (kw), 记为(pk,sk)←Keygen(pp,parameters).

(3) 密文生成算法 Enc: 输入 pk 和消息序列 (m1,··· ,mq), 运行 VC.Com 算法(C,aux) ← VC.Com((m1,··· ,mq),parameters), 输出数据密文 C,C0, 记为 (C,C0) ←Enc(pk,(m1,··· ,mq)).

(4) 抽样算法Sample: 数据消费者与数据持有者进行交互,数据消费者挑战第i 位的消息mi. 数据持有者运行VC.Open 算法Λi←VC.Open(i,mi,aux) 输出对应消息的证明Λi, 记为(Λi,mi) ←Sample(i,mi,aux).

(5) 验证算法Ver: 数据消费者运行VC.Ver 算法验证是否VC.Ver(C,i,mi,Λi)=1, 如果有效输出1; 否则, 输出0.

(6) 解密算法Dec: 数据消费者、数据持有者与区块链进行交互, 数据消费者部署智能合约进行有条件的付费, 数据持有者发布解密密钥sk, 区块链执行智能合约, 验证合约执行算法. 之后, 数据消费者与区块链交互, 解密消息(m1,··· ,mq), 记为(m1,··· ,mq)←Dec(sk,(C,C0)).

安全目标: 基于机器学习的公平数据交易协议应满足如下安全目标:

完备性: 如果数据持有者和数据消费者诚实执行协议, 协议完成, 数据持有者将获得付费, 同时数据消费者获得有效的数据.

公平性: 协议执行使得数据持有者获得付费, 同时数据消费者获得有效的数据, 要么两方都不能获得.

机密性: 公平数据交易协议应满足机密性要求, 对于未进行抽样的数据, 无法获得数据的任何信息, 即未付费的外部敌手不能获得除抽样数据外售卖数据的任何信息.

4 基于机器学习的公平数据交易协议

4.1 基于机器学习的公平数据交易协议构造

本节给出具体的基于机器学习的公平数据交易协议, 协议流程如图2 所示.

数据消费者与数据持有者协商数据定价, 本文假设数据价格为固定值, 数据持有者与数据消费者分别持有ECDSA 密钥对, 记为(pkh,skh),(pkc,skc). 数据持有者与数据消费者交互执行协议. 首先, 初始化系统参数pp, 数据持有者生成(pk,sk), 并发送pk 给数据消费者. 数据消费者向数据持有者表明需要购买的数据, 发送对需求数据的描述d 给数据持有者, 数据持有者根据描述d, 加密数据(m1,··· ,mq), 将密文(C,C0) 发送给数据消费者. 数据消费者对消息mi进行抽样, 数据持有者生成相关证明. 数据消费者运行BP 神经网络算法对数据进行决策, 数据消费者发布公平数据交易智能合约到区块链网络, 数据持有者调用智能合约, 释放解密密钥sk 接收付款, 数据消费者对密文进行解密, 获得相应数据. 具体协议如下:

初始化Setup: 数据持有者与数据消费者进行交互, 运行Setup 算法初始化系统参数, 选取抗碰撞哈希函数H :{0,1}∗→Zp,H0:{0,1}∗→Zp, 输出公开参数pp=(H,H0).

密钥生成Keygen: 数据持有者运行VC.Keygen 算法(parameters) ←VC.Keygen(1k,q) 生成公开参数. 令G,GT为两个双线性群阶为素数p,存在双线性映射e:G×G →GT,令g ∈G 为群G 的生成元.数据持有者选取随机数x1,··· ,xq∈Zp, 对于i = 1,··· ,q, 计算hi= gxi. 同时对于i,j = 1,··· ,q(i ̸=j), 计算hi,j= gxixj. 数据持有者选取随机数kw∈Zp, 输出pk = (g,{hi}i=1,···,q,{hi,j}i,j=1,···,q,i̸=j),sk=(kw).

算法1 Transfer 算法Input: input parameters(Z,K′,S,s,pkh,pkc)Output: output result 1 if Z = K′ ·S then 2 Transfer s to pkh 3 end 4 else 5 Withdraw s to pkc 6 end

算法2 Refund 算法Input: input parameters (s,pkc)Output: output result 1 Withdraw s to pkc

4.2 安全性分析

引理1 基于机器学习的公平数据交易协议满足完备性.

证明: 数据持有者与数据消费者诚实地执行4.1节中描述的数据交易协议, 初始化系统参数, 数据消费者部署智能合约, 数据持有者通过释放正确的密钥kw, 智能合约转账至数据持有者公钥地址, 同时数据消费者获得解密密钥, 对密文进行解密, 获得消息(m1,··· ,mq).

引理2 基于机器学习的公平数据交易协议满足公平性.

证明: (1) 数据持有者是恶意的, 数据消费者是诚实的, 分两种情况进行讨论. ①不提交解密密钥kw或提交错误密钥kw的情况下获得付款. 在这种情况下, 根据公平数据交易智能合约执行, 不提交解密密钥kw, 数据消费者可调用Refund 算法, 取回押金; 提交错误密钥kw, Z = K′·S 无法通过验证, 智能合约退还押金给数据消费者. ②数据持有者不提供可靠数据情况下获得付款. 数据提供者不提供可靠的数据, 数据消费者随机挑战消息, 使用BP 神经网络来进行决策. 数据消费者不部署智能合约, 数据持有者不能获得付款.

(3) 数据持有者与数据消费者均为恶意的. 根据协议执行, 数据消费者发布智能合约到区块链网络, 数据持有者拒不发送解密密钥, 数据消费者不调用Refund 算法, 取回押金, 双方进入僵持状态, 在这种情况下, 双方占用网络带宽, 消耗自身资源, 这对恶意的双方是公平的. 我们认为理性的数据持有者和数据消费者会有效执行协议, 避免浪费自身资源. 因此, 提出的基于机器学习的公平数据交易协议满足公平性.

引理3 基于机器学习的公平数据交易协议满足机密性.

证明: 数据持有者与数据消费者进行链下通信, 采用安全信道通信, 数据持有者借助向量承诺发送密文C,K,c,zi,i∈[1,···,q]给数据消费者, 因此, 不会泄漏数据的任何信息. 针对链上交易, 外部敌手可以验证是否Z = K′·S, 由哈希函数H0的抗碰撞性, 敌手无法恢复cmi,i ∈[1,··· ,q], 因此, 不会泄漏(m1,··· ,mq) 的任何信息.

4.3 性能分析

本节讨论协议的执行效率, 并结合以太坊部署智能合约, 评估公平交换协议的Gas 消耗. 首先对本文密码算法的执行效率进行评估, 使用intel(R) Core(TM) i5-2450M CPU 2.50 GHz 4.00 GB 内存电脑执行1000 次, 基于Miracl 库[30]对算法进行仿真实验, 包括协议的Keygen, Enc, Sample, Ver, Dec 算法,同时针对Sample 算法, 选取不同的挑战块进行评估. 各算法的执行时间如图3 和图4 所示. 图3 中随着消息序列承诺值q 的增长, Keygen 算法增长较快, Enc, Sample, Ver 和Dec 算法, 增长平缓. 如图4 所示,在q 值不变时, Sample 算法执行时间随着挑战块的数量增加而增长.

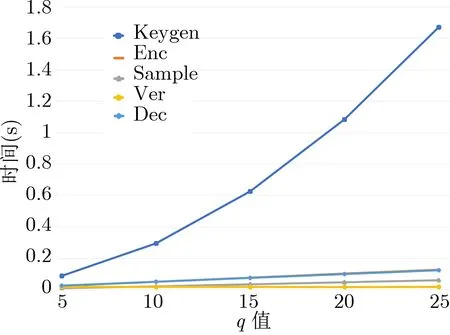
图3 各算法执行时间Figure 3 Time cost of algorithms

采用MATLAB 6.5 版本运行BP 神经网络, 由输入层, 隐藏层1, 隐藏层2 和输出层组成. 输入层中的节点数与文本标签的数量相同, 输出层中有一个值为0 或1 的节点. 在隐藏层1 和隐藏层2 中分别设置5 和25 个节点. 如果样本分类正确, 则BP 神经网络的输出为1. 否则, BP 网络的输出为0. 传递函数设置为tansig 和purelin, 而训练函数设置为trainlm. 当误差函数降低到10−8以下时, 则训练停止. 在程序实现中, 通过newff 函数构建BP 神经网络. 使用34 组数据对BP 神经网络进行训练, 包括20 组阿尔茨海默病例和14 组其他疾病文档中抽取标签. 分别以只包含症状的5 个关键字, 以及包含症状、用药、治疗方案的30 个关键字为输入训练神经网络, 分别得到如图5 所示模型. 使用7 个测试用例对训练模型进行测试, 发现模型的准确度从71.4%(5/7) 提升到100%(7/7).

本文采用Solidity 语言编写智能合约, 并通过以太坊钱包进行实际部署, 公平交换协议的Gas 消耗如表2 所示. 由于Transfer 算法需要进行执行验证, 所以消耗Gas 比Refund 算法多.

图5 BP 神经网络模型Figure 5 BP neural network model

Function Gas 消耗Deploy 1517852 Transfer 396099 Refund 21000

5 总结

针对已有数据交易协议无法保证数据交易的公平性和交易数据的可靠性, 本文提出基于机器学习的公平数据交易协议, 利用区块链技术去中心化优势, 结合向量承诺和BP 神经网络, 使得数据消费者可对抽样数据进行有效验证, 保证数据的可靠性, 同时借助智能合约实现原子交换的公平性. 实验验证基于机器学习的公平数据交易协议的实用性.