基于数学建模的热辊牵伸过程研究
马 睿
(陕西工业职业技术学院,陕西咸阳712000)
在高强锦纶6 长丝制备过程中,纤维在热辊之间的拉伸性能变化与牵伸工艺参数较为密切,虽然目前国内的科研工作者在纤维拉伸性能方面做出了大量工作[1],但是集中度还仅限于牵伸过程的结构变化和牵伸方法变化[2],而对牵伸工艺参数的作用机理研究较少[3-4]。在高强锦纶6 纤维的牵伸过程中,牵伸工艺参数对其最终性能会产生较大影响[5-6],如果采用试验来完成工艺参数优化,将会浪费大量的人力和物力,而采用数学模拟的方法则可以准确得到特定工艺参数下牵伸工艺参数对纤维牵伸后性能的影响。
1 数学建模
1.1 基本假设
高强锦纶6 长丝牵伸过程的基本假设前提包括[7]:(1)第一个牵伸辊和第二个牵伸辊之间的纤维运动不受周围介质热作用的影响,此时纤维的温度与第二个牵伸辊相当;同理,第二个牵伸辊和第三个牵伸辊之间的纤维运动不受周围介质热作用的影响,此时纤维的温度与第三个牵伸辊相当,即假设高强锦纶6 长丝的牵伸过程为等温牵伸;(2)高强锦纶6 长丝牵伸过程中的丝条张力恒定不变,忽略惯性力以及其他介质阻力作用;(3)高强锦纶6 长丝牵伸过程中纤维保持稳态形变;(4)高强锦纶6 长丝牵伸过程中的纤维没有受到压缩。
1.2 基本方程
基于力平衡方程、质量守恒方程和牵伸本构方程等建立了高强锦纶6 长丝牵伸过程中的数学模型[8-9],具体包括:
(1)质量守恒方程:W=ρVA =常量
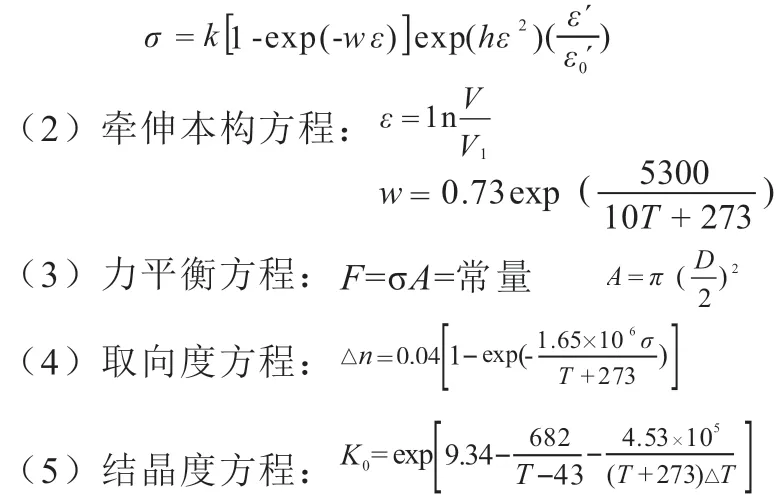
上述5 个方程式中:W 为纤维质量,ρ 为纤维密度,V 为距离第一个牵伸辊的位置X 处的速度,A 为纤维剖面面积,D 为纤维直径,σ 为纤维受到的应力,w 为粘弹系数,h 为应变硬化因子,V1为第一个牵伸辊转动的速度,T 为温度,△n 为双折射率,F 为张力,K 为结晶速率常数[10],将方程式(1)~(3)进行联立,可得应变ε 和卷绕长度的关系式如下:
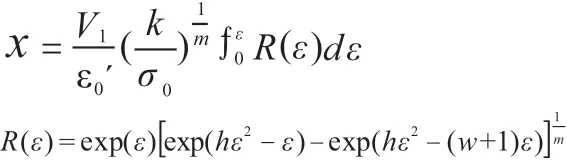
式中,σ0为纤维的初始应力、m 为应变敏感系数[11]。
在进行高强锦纶6(PA6)长丝牵伸过程的拉伸模拟时,根据国内某大型纺织企业的牵引工艺参数进行了模拟,其中GR1、GR2 和GR3 分别表示第一个牵伸辊、第二个牵伸辊和第三个牵伸辊。本文主要针对的是第一个牵伸辊和第二个牵伸辊,以及第二个牵伸辊和第三个牵伸辊之间的牵伸过程进行模拟,分别表示一级牵伸过程和二级牵伸过程模拟。
2 结果及讨论
2.1 一级牵伸过程模拟
图1 为第一个牵伸辊和第二个牵伸辊之间的卷绕长度与应力和应变的关系曲线。从应力- 卷绕长度曲线来看,高强锦纶6 长丝牵伸过程中的应力与卷绕长度存在正相关性,随着卷绕长度逐渐增大,应力呈现先缓慢增大而后趋于稳定的趋势,且在卷绕长度40cm~80cm 范围内,应力增加速率较大;从应变- 卷绕长度曲线来看,高强锦纶6 长丝牵伸过程中的应变与卷绕长度的变化趋势与应力- 卷绕长度曲线相似,即纤维的应变也呈现随着卷绕长度增加先增加而后趋于稳定的特征,在卷绕长度介于30mm~70mm 范围内时,应变增加速率较快。
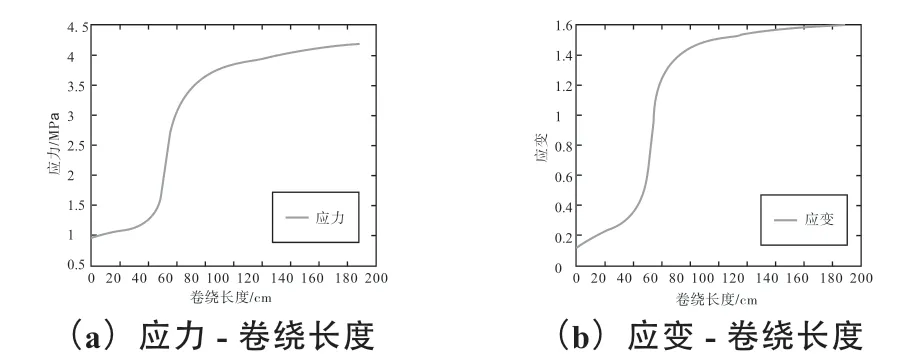
图1 第一个牵伸辊和第二个牵伸辊之间的卷绕长度与应力和应变的关系曲线Fig.1 Winding length versus stress and strain curve between the first draft roller and the second draft roller
图2 为第一个牵伸辊和第二个牵伸辊之间的卷绕长度与牵伸速度和纤维直径的关系曲线。从牵伸速度- 卷绕长度曲线来看,高强锦纶6 长丝牵伸过程中的牵伸速度与卷绕长度存在正相关性,随着卷绕长度逐渐增大,牵伸速度呈现先缓慢增大而后趋于稳定的趋势,且在卷绕长度40cm~80cm 范围内,牵伸速度增加速率较大;从纤维直径- 卷绕长度曲线来看,高强锦纶6 长丝牵伸过程中的纤维直径与卷绕长度的变化趋势表现出明显不同特征,即纤维的直径会随着卷绕长度增加先减小而后趋于稳定的特征,在卷绕长度介于20cm~80cm 范围内时,纤维直径减小速率较快。
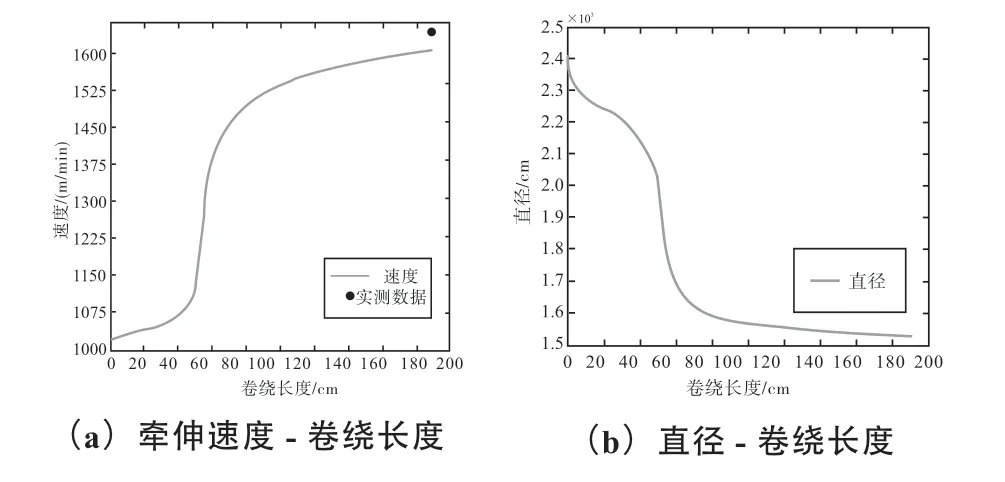
图2 第一个牵伸辊和第二个牵伸辊之间的卷绕长度与速度和直径的关系曲线Fig. 2 Winding length vs. speed and diameter curve between the first draft roller and the second draft roller
图3 为第一个牵伸辊和第二个牵伸辊之间的卷绕长度与双折射率和结晶度的关系曲线。从双折射率- 卷绕长度曲线来看,高强锦纶6 长丝牵伸过程中的双折射率与卷绕长度存在正相关性,随着卷绕长度逐渐增大,双折射率呈现先缓慢增大而后趋于稳定的趋势,且在卷绕长度50cm~90cm 范围内,双折射率增加速率较大;从结晶度- 卷绕长度曲线来看,高强锦纶6 长丝牵伸过程中的结晶度与卷绕长度的变化趋势与双折射率- 卷绕长度曲线相似,即纤维的结晶度也呈现随着卷绕长度增加先增加而后趋于稳定的特征,在卷绕长度介于50cm~90cm范围内时,结晶度增加速率较快。
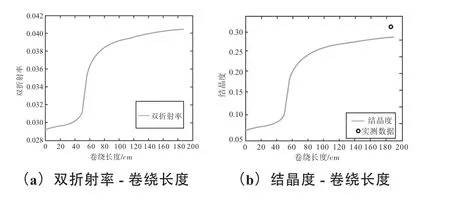
图3 第一个牵伸辊和第二个牵伸辊之间的卷绕长度与双折射率和结晶度-的关系曲线Fig. 3 Winding length versus birefringence and crystallinity- between the first and second draft rolls
2.2 二级牵伸过程模拟
图4 为第二个牵伸辊和第三个牵伸辊之间的卷绕长度与应力和应变的关系曲线。从应力- 卷绕长度曲线来看,高强锦纶6 长丝牵伸过程中的应力与卷绕长度存在正相关性,随着卷绕长度逐渐增大,应力呈现先缓慢增大而后趋于稳定的趋势,卷绕长度250cm 范围内的应力从13MPa 增加至42MPa,丝条在出第三个牵伸辊时的应力约为40MPa;从应变- 卷绕长度曲线来看,高强锦纶6 长丝牵伸过程中的应变与卷绕长度的变化趋势与应力- 卷绕长度曲线相似,即纤维的应变也呈现随着卷绕长度增加先增加而后趋于稳定的特征,在卷绕长度介于20cm~70cm 范围内时,应变增加速率较快,卷绕长度250cm 范围内的应变从0.2 增加至1.6。
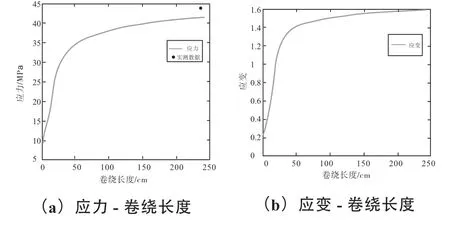
图4 第二个牵伸辊和第三个牵伸辊之间的卷绕长度与应力和应变的关系曲线Fig. 4 Winding length versus stress and strain curve between the second draft roller and the third draft roller
图5 为第二个牵伸辊和第三个牵伸辊之间的卷绕长度与牵伸速度和纤维直径的关系曲线。从牵伸速度- 卷绕长度曲线来看,高强锦纶6 长丝牵伸过程中的牵伸速度与卷绕长度存在正相关性,随着卷绕长度逐渐增大,牵伸速度呈现先缓慢增大而后趋于稳定的趋势,卷绕长度250cm 范围内的牵伸速度从1820m/min 增加至5220m/min;从纤维直径-卷绕长度曲线来看,高强锦纶6 长丝牵伸过程中的纤维直径与卷绕长度的变化趋势表现出明显不同特征,即纤维的直径会随着卷绕长度增加呈先减小而后趋于稳定的特征,卷绕长度250cm 范围内的纤维直径从1.36cm 减小至1.02cm。
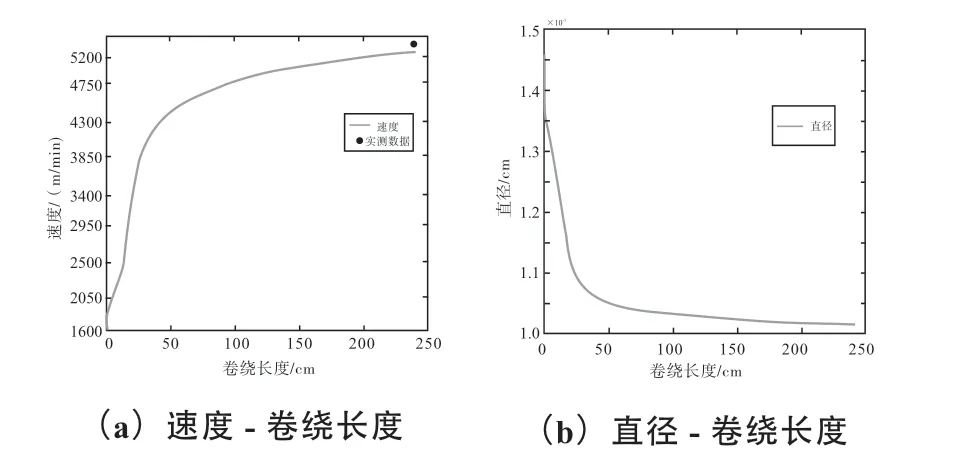
图5 第二个牵伸辊和第三个牵伸辊之间的卷绕长度与速度和直径的关系曲线Fig. 5 Winding length vs. speed and diameter curve between the second draft roller and the third draft roller
图6 为第二个牵伸辊和第三个牵伸辊之间的卷绕长度与双折射率和结晶度的关系曲线。从双折射率- 卷绕长度曲线来看,高强锦纶6 长丝牵伸过程中的双折射率与卷绕长度存在正相关性,随着卷绕长度逐渐增大,双折射率呈现先缓慢增大而后趋于稳定的趋势,卷绕长度250cm 范围内的双折射率从0.044 增加至0.054;从结晶度- 卷绕长度曲线来看,高强锦纶6 长丝牵伸过程中的结晶度与卷绕长度的变化趋势与双折射率 - 卷绕长度曲线相似,即纤维的结晶度也呈现随着卷绕长度增加先增加而后趋于稳定的特征,卷绕长度250cm 范围内的结晶度从0.34 增加至0.62。
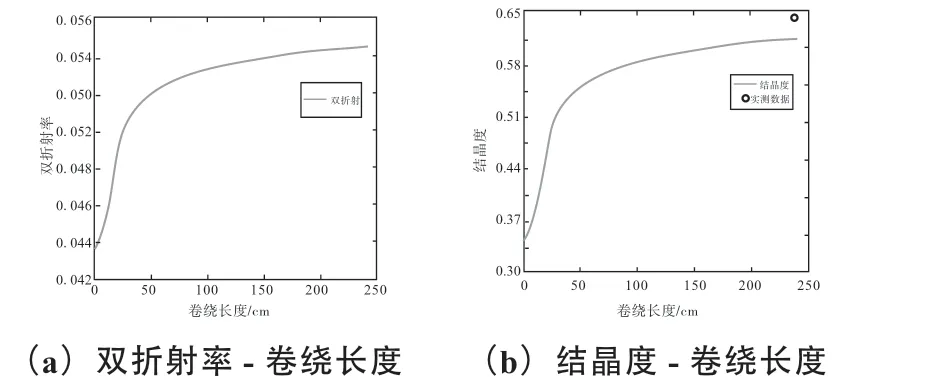
图6 第二个牵伸辊和第三个牵伸辊之间的卷绕长度与双折射率和结晶度的关系曲线Fig. 6 Winding length vs. birefringence and crystallinity between the second and third draft rolls
第二个牵伸辊和第三个牵伸辊之间的丝条出第三个牵伸辊时,丝条速度为 5271m/min,而本文的数学模拟得到的丝条速度为 5220 m/min;第二个牵伸辊和第三个牵伸辊之间的丝条出第三个牵伸辊时,第三个牵伸辊与卷绕辊之间的卷绕应力为 42MPA,而本文的数学模拟得到的卷绕应力为40MPa;第二个牵伸辊和第三个牵伸辊之间的丝条出第三个牵伸辊时,高强锦纶 6 成品丝的结晶度为 0.63,而本文的数学模拟得到的高强锦纶 6 成品丝的结晶度为 0.61。由此可见,第二个牵伸辊和第三个牵伸辊之间的丝条速度、卷绕应力和结晶度测试结果与模拟结果基本吻合。
3 结论
(1)第一个牵伸辊和第二个牵伸辊之间,以及第二个牵伸辊和第三个牵伸辊之间的应力、应变、牵伸速度、纤维直径、双折射率和结晶度与卷绕长度的对应关系基本相同,只是第二个牵伸辊和第三个牵伸辊之间的牵伸参数的变化速度相对第一个牵伸辊和第二个牵伸辊之间更加缓慢。可见,高强锦纶6 长丝制备过程中需要多个不同牵伸区来实现高质量和高性能。
(2)第二个牵伸辊和第三个牵伸辊之间的丝条出第三个牵伸辊时,实测丝条速度、卷绕应力和成品丝结晶度分别为 5271 m/min、42MPa 和0.63,而本文的数学模拟得到的丝条速度、卷绕应力和成品丝结晶度分别为5220 m/min、40MPa 和0.61,第二个牵伸辊和第三个牵伸辊之间的丝条速度、卷绕应力和结晶度测试结果与模拟结果基本吻合。

