单圈图的Wiener指标研究

邵 云

（滁州城市职业学院教育系，安徽滁州 230039）

分子的拓扑性质是分子的固有性质之一，而分子拓扑指标则反映了分子的性能。分子拓扑指标有多种，其中Wiener是最重要的拓扑指标，1947年由化学家H.Wiener提出，广泛应用于统计化学、结构化学、有机化学和药物合成方面[1]。单圈图指一个连通图具有相同的顶点数和边数[2]。而Wiener指标是连通图中所有两点之间的距离和[3]。本文就对单圈图Wiener指标的极值和边平均Wiener指标进行研究，为Wiener的应用提供理论参考。

1 Wiener指标[4]

设图G=(V(G),E(G))，其中V(G)、E(G)分别表示图G的顶点集和边集。令dG(u,v)表示图中两个顶点u、v之间的距离，定义

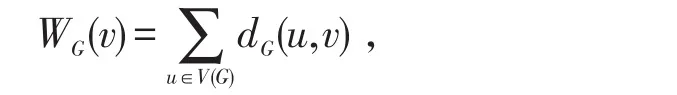
则图G的Wiener指标W(G)为

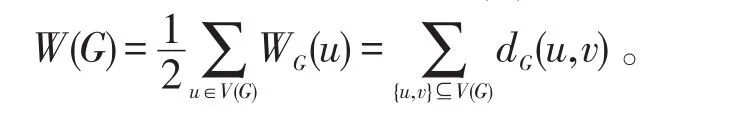
2 单圈图Wiener指标的极值

2.1 最小（大）Wiener指标

①对于n阶单圈图G，当且仅当G≅A(n,3)时，W(G)获得最小值n2-2n[3]。

②当单圈图G的阶数n＞5时，如果，那么

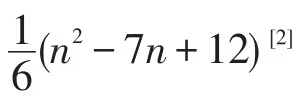
2.2 次小（大）Wiener指标

①设G为具有n个顶点的单圈图，则当且仅当G≅A(n,4)或H1，W(G)获得第二小值n2-n-4[3]。

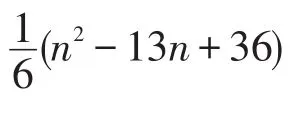
2.3 第三小（大）Wiener指标

2.4 第四小（大）Wiener指标[6]

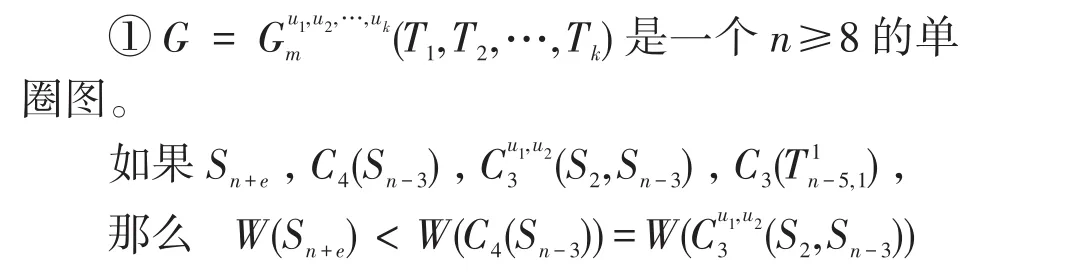
3 n阶单圈图的边平均Wiener指标

图G的边平均Wiener指标由WU Baoyindureng[7]首次引进，用W′e(G)来表示。

其中D′(f,g)是两条边f和g之间的平均距离。

对于一个顶点数为n的单圈图G，其圈长为m，对于连通图G，两条边f=uv和g=xy的距离D(f,g)为边f和边g两个顶点之间的最短距离。其中

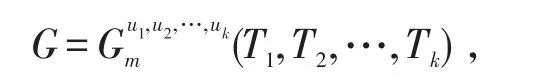
此时边平均Wiener指标取整数的充要条件是：当且仅当4|m时，G的边平均Wiener指标就取整数[8]。

3.1 最小（大）边平均Wiener指标[9]

对于n阶单圈图，当n≥6，等号成立当且仅当G≅C3(Pn-2)时，边平均Wiener指标取最小值的条件为

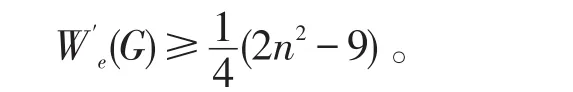
等号成立当且仅当G≅C3(Pn-2)，边平均Wiener指标取最大值的条件为

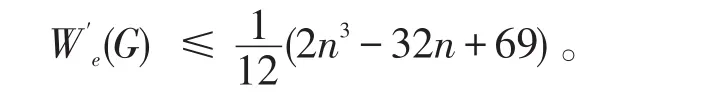
3.2 次大边平均Wiener指标[10]

对于顶点数n＞10的单圈图，如果不同构，此时

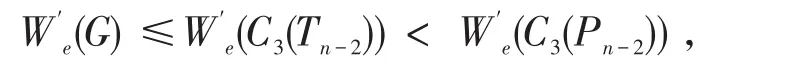
当等号成立时，C3(Tn-2)是具有次大边平均Wiener指标条件。

3.3 第三小（大）边平均Wiener指标

对于n阶单圈图，与不同构，当n＞8时，有

4 结语

Wiener指标在单圈图中有着广泛研究。本文对最小（大）、次小（大）、第三小（大）、第四小（大）Wiener指标，以及最小（大）边、次大边、第三小（大）边平均Wiener指标进行系统论述，有助于Wiener指标的更广泛应用。