物体的平衡 力的动态分析方法探究

摘 要：物理学是当今最精密的一门自然科学学科，大到宏观世界，小到微观粒子，它以实验为基础，研究物质运动最一般规律和物质基本结构的学科，学好高中物理力学部分是学好整个高中物理的基础和关键，多数学生生活经验较少，在学习力学的时候无从下手，对抽象问题难于理解，而对力的分析至关重要，它涉及到物体的静态平衡和动态平衡，我们在这里阐述力的动态分析的几种方法，封闭三角形法、相似三角形法、圆周旋转法，平行四边形法、正交分解数学法以及整体隔离法.

关键词：封闭三角形法;相似三角形法;圆周旋转法;正交分解数学法;整体隔离法

中图分类号：G632      文献标识码：A      文章编号：1008-0333（2020）34-0085-02

收稿日期：2020-09-05

作者简介：李志永，硕士，从事高中物理教学研究.

通过这些年对初高中教学的研究知道，高中与初中的物理教材相比，高中教材的知识量比初中的大得多，拿力学部分而言，初中的知识点约60个，而高中力学知识点增为90个，并且理论性增强，这是最主要的特点.初中教材有些只要求初步了解，只作定性研究，而高中则要求深入理解，作定量研究，教材的抽象性和概括性大大加強，对于基础差的学生学好高中物理并不容易.

而力学的动态分析部分学生往往掌握的比较差，对方法理解不到位，用的比较乱，这样就很容易做错，今天我们在这里讲述多种解题方法，解决动态分析中绝大多数问题，如果加以综合运用几乎都能解决.

一、力的动态分析方法探究

1.封闭三角形法

对于动态分析首先要想到封闭三角形法，封闭三角形法顾名思义要有三个力，对研究对象受力分析满足以下条件即可应用.

（1）第一个力是恒力，即大小方向都始终不变的力，比如重力.

（2）第二个力方向始终不变，比如支持力.

用法：如果满足上述两条，我们平移三个力，使这三个里构成一个首尾顺次相接的三角形，按照顺时针或者逆时针的方向旋转第三个力，通过线段的长短的变化来判断力的大小变化.

注意：在旋转的过程中一定要保持恒力不能发生变化，这里面也是最容易发生错误的地方.

例题1 如图1所示，不计一切摩擦，OA为自由绕着A点转动的杆，O点栓一细绳挂一个重物，绳子末端C沿着圆弧旋转到B的过程中（OA杆倾角θ保持不变）各个力的变化.

OA为活动杆，受力一定沿着杆的方向，平移成首尾相接的动态分析图如图2、图3两种画法所示，保持重力大小不变，逆时针方向旋转第三个力发现，两种画法支持力逐渐减小，绳的拉力先减小后变大.

2.相似三角形法

如果上述方法条件不适用，我们可以考虑相似三角形法，多适用于一个或两个力大小方向的变化， 使用方法：

（1）找到两个三角形，其中的一个三角形只代表各个边长，称之为“几何三角形”

（2）对研究对象受力分析，平移力得到一个首尾顺次相接的“力的三角形”

（3）根据比例列方程求解

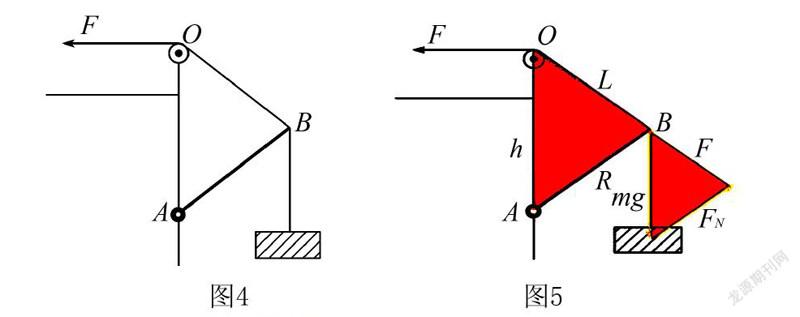
例2 如图4，A点是自由转轴，0点为一滑轮，B点系一细绳并拴着一个物块，不计一切摩擦，用力沿着水平方向向左拉动，拉动过程中拉力与杆的支持力如何变化.

图4可以看出直接得到一个ΔOAB，称为几何三角形，如图5中的红色三角形;在B点受力分析平移成首尾相接三角形如图5黄色三角形，各边代表力.根据相似得到方程.

拉动过程中R不变，FN保持不变，L变短，F减小.

3.圆周旋转法

条件：（1）一个力的大小和方向始终不变（如重力）

（2）另外两个力的夹角保持不变

用法： 把三个力平移到一个圆内构成一个首尾 顺次相接的内接三角形，旋转夹角不变的两 个力，通过线段长短判断力的大小.

注意： 旋转过程中线段是否过直径，作图时候严格按照题干要求仔细画图

例题3 如图6，一个75°的V型架子，右边MO与水平成30°角，左边MN与水平成60°角，内部放一个光滑的小球，整个系统顺时针方向转30°，判断MO挡板和MN挡板对小球的支持力FN1和FN2的大小变化.

图6 是小球受力情况，把这三个力平移到一个圆内，如图7红色线条，FN1，FN2都沿着顺时针方向转动，FN1转动过程中经过了直径，代表FN1这个力先增大后减小，FN2直接变短代表力直接减小.

例题4 如图一个质量为m的小球用细绳拴住并悬挂在正方体的两边上，沿着顺时针方向缓慢旋转90度的过程中，两段绳子的拉力变化.

为什么要放在一个圆内，因为重力不变，在圆内就是一个固定的弦，在旋转过程中同一条弦所对用的圆周角保持不变，也就间接反映两个力的夹角保持不变，这里就是注意图的画法，顺时针转很小角度平移三个力到圆内构成一个首尾顺次相接的三角形，如图10红色三角形所示，顺时针旋转90度的过程后，F2恰好达到水平，在这个过程中，F1对应的线段变长，代表F1这个力一直变大，F2对应的线段先变长到直径位置在变短，代表F2这个力先变大后变小.

4.正交分解数学法

有一些题型用上面三种方法都无法解决，根据生活经验和数学方法可以求解特殊题型.

例题5 如图11所示，在固定好的水平和竖直的衣架上，A、B两点连接着一根绕过光滑的轻小滑轮的不可伸长的细绳，重物悬挂于滑轮下，在移动A，B两点过程中力的变化情况？

对于光滑的滑轮绳子两侧拉力相等设为F，受力分析如图12所示，设两端绳子与y轴之间的夹角分别为α和β，左右两段绳长分别为L1和L2，绳总长为L，左右两侧水平长度分别为d1和d2，总宽度为d，由平衡条件和几何关系可得：

总宽度d和总长度L不变，角度α不变，A移动到A′的过程中， α不变，F 不变;B移动到B′的过程中，间距d变大，α变大，F变大.

5.平行四边形法和整体法与隔离法

在研究三个力的时候通常只有一个力为恒力的条件的时候，另两个力的合力一定和这个恒力等大反向，我们可以用画平行四边形比较简单，那就是以恒力等大反向的力作为平行四边形的对角线，以另两个力为邻边画平行四边形，一般在不同的位置画两个或以上的平行四边形，通过邻边长短来判断力的大小变化.

整体法与隔离法是需要结合上述五种方法的一种综合运用法，也就是说确定好研究对象是单个物体还是当成一个整体研究，根据不同的条件运用不同的方法就可以解决.

总之力的动态分析对于初学者或者是学过的学生分析起来都不算容易，原因之一是很多学生并没有掌握各种方法的适用条件，如果知道了各种方法的适用条件，对症下药多加以练习，积累解题经验，力的动态分析便会了如指掌.

  参考文献：

[1]赵淑波，卢焱，王红娟.解题决策[M].长春：东北师范大学出版社，2014.[2]张慧爱.试论高中物理力学知识的生活化教学[J].现代阅读（教育版），2013（02）：258.

[3]王济焜.高中物理解题技巧及解题能力提升[J].中学生数理化（学习研究），2016（08）：27.

[4]崔蓓.高中物理力学学习技巧之我见[J].亚太教育，2016（36）：85.

[责任编辑：李 璟]