基于广义线性回归的高速公路事故预测模型
徐永利 李景军 王以龙

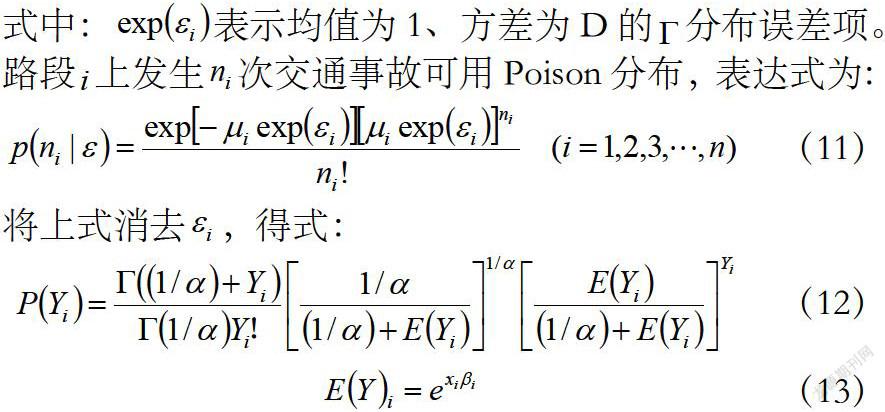


摘 要:高速公路网的日益完善,通车数量的急剧增加,目前交通事故的发生已成为高速公路通行中的一大难题。为了确定各因素对事故的影响程度,提高事故规律分析及预测的准确性,提出通过建立广义线性回归模型对高速公路进行事故预测。首先通过挖掘高速公路的历史事故数据,对影响事故的多个因素进行定量分析,建立负二项回归方程,其次验证各因素的拟合优度,最后进行事故预测,结果表明模型提升了事故预测的准确性。
关键词:广义线性回归模型;高速公路;事故预测
中图分类号:U491.3 文献标识码:A
0 引言
根据山东省统计局官方网站统计,2018年山东省道路交通事故共发生13 226起,死亡人数为3 600人。而山东省截止到2018年,在汽车拥有量、道路面积、通车里程都持续增加的情况下,道路交通安全呈整体稳定的趋势。
1 事故预测模型选择
1.1 Poison分布模型
Poison分布作为回归模型最基础、最常用的模型,事故量选用Poison分布模型预测时,数据的均值和方差是相等的,采用该分布模型描述事故发生的规律,表达式如下:
式中:表示路段发生次事故的概率;表示路段发生的事故次数的数学期望;表示路段的解释变量;表示解释变量的系数。
由于道路交通事故数据难以满足Poison分布对数据的要求,模型的应用具有局限性。
1.2 负二项分布模型
结合事故数据的特点,将Poison分布模型消除均值等于方差带来的影响,即成为负二项分布模型。如式*:
式中:表示路段上发生的交通事故率;表示路段上發生的交通事故率的期望值;表示离散度指数;表示模型的解释变量;表示解释变量的参数。
1.3 零堆积Poison分布和零堆积负二项分布模型
如果划分路段内无事故发生时,会导致数据过度离散,将无法使用Poison分布模型和负二项分布模型。
事故次数分布服从Poison分布和负二项分布,由于均值远小于方差,因此选用负二项模型进行事故预测较为合适。
2 事故数据准备
2.1 路段划分
使用微观模型预测事故时首先需要将路段进行单元划分,为研究交通流与事故之间的关系,选取济乐高速南延段作为研究对象,该路段的道路设计为双向四车道,最高速度不超过100 km/h,将道路每1 km视为一个路段,共50个样本路段。
2.2 自变量选取
选择交通流数据作为模型的自变量,研究各路段中固定检测器所采集的数据,统计为表1。
3 负二项事故预测模型建立
由于交通流参数的不同,路段的事故期望值可看作交通流参数的函数,表达式为:
4 模型结果分析
通过对济乐高速南延段事故数据和交通流数据的分析,选用SPSS17.0对多个数据进行回归拟合,显著性水平设为0.05,采用逐步回归的方法,参数估计结果见表2和表3。
从表中弹性系数一列看各个因素的值,3个参数的弹性值均大于0,说明与交通事故发生次数是呈正相关的,其中路段平均占有率弹性系数值最大,说明对事故发生次数影响最大。
济乐高速南延段交通事故期望值为:
其中:为年平均日交通量;为路段平均占有率;为大中型车占比。
将2019年该路段的交通流数据,代入上述所标定的模型,所得相对误差为7.6%,证明所建立的事故预测模型具有较高的精度。
5 结语
论文根据历史事故数据的分布规律,对多个影响因素进行量化,建立负二项回归模型,研究各因素对交通事故的影响程度,使得预测结果更为准确。
参考文献:
[1]陈长坤,武艳,辛梦阳,等.基于广义线性模型的干线公路交通事故预测[J].公路与汽运,2015(06):56-59.
[2]童伟,杨凡.基于SVR的成都市交通事故态势分析[J].农家参谋,2018(12):287.
[3]王小凡,朱永强.基于灰色BP神经网络模型的道路交通事故预测[J].白城师范学院学报,2019,33(06):36-40+51.

