汽配件制造业中的喷涂工艺生产排程研究

肖峰 尹如意

摘要：为提高汽车配件生产效率、降低生产成本，对汽车配件喷漆工艺中的涂料与支架进行动态调配。以中等批量生产为例，建立生产时间与配件种类、配件喷涂颜色、配件喷涂数量、支架种类、支架数量之间的数学模型。进而以生产效率为优化目标，在限定支架数量和满足生产工艺的条件下采用贪心算法对模型进行优化求解，得到完成期望生产量（7831个配件）喷涂的最少时间以及最小换色次数分别为44个小时、11次。研究结果表明贪心算法可以实现汽车配件喷涂工艺的生产排程最优化，是解决资源组合规划问题和提高企业生产效率、降低企业生产成本的有效方法。

关键词：生产排程;贪心算法;动态规划;资源组合;汽车配件

0  引言

当前，新科技和新技术不断兴起，全球工业体系、发展模式和竞争格局迎来重大变革[1]。世界各国纷纷出台以先进制造业为核心的“再工业化”国家战略，我国也于2015年也推出发展智能制造的战略举措—“中国制造2025”国家战略。由此可见，智能制造已成为制造业发展的重要方向，成为世界各国先进制造业的制高点[2]。在这样的时代背景下，世界各国汽车企业纷纷通过智能技术的应用及产业链的变革来实现汽车产业转型。汽车配件喷涂工艺作为汽车生产的重要环节，对汽车企业乃至整个汽车产业都有重要影响，而对喷涂工艺进行优化是提高生产效率和企業利益的重要措施。

为了提高工业生产效率，大量学者对生产过程中的工艺优化问题进行了研究。陆超引入工序解耦点对多品种小批量复杂零件进行了工序优化[3]，陈梓祥利用APS优化技术对制造业生产线调度系统进行了设计[4]，吴思旻则通过精益生产理论来提高汽车零部件企业生产效率[5]。为了对某一批次汽车配件喷涂工艺进行优化，文章从效率角度深入考虑，探索短期内最优策略的制定，以便汽车企业能够实时调整工艺排程，实现生产的高效化和低成本化。

1  配件喷涂工艺流程

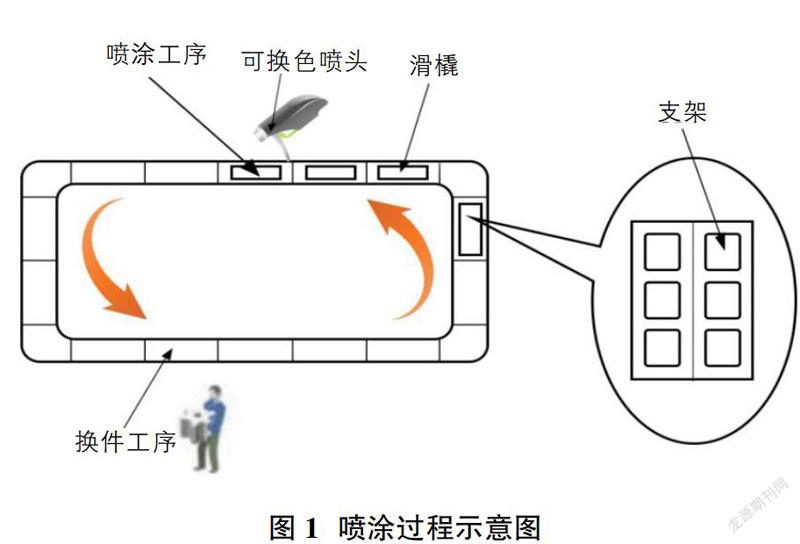
配件喷涂工艺流程如图1所示。待喷涂配件（注塑缓存件）置于滑撬上，经底漆（黑底/白底）—面漆（15 种左右）—清漆（高光/哑光）三道工序后，完成整个喷涂作业。配件成品最终颜色由面漆决定，每种面漆有对应的底漆和清漆颜色;而每个滑橇上可放置6个支架，一次最多可完成6个配件的喷涂。

1.1 喷枪换色过程

前后相邻两个滑橇上的配件需要喷涂不同的面漆色，对应的喷枪则需要更换涂料颜色。该换色过程要求在两个滑橇之间插入一个滑橇的任意个只喷涂底漆的底漆件作为过渡，作为售后备件使用。

任意红色和任意蓝色面漆后面不能接任何白色面漆，极地白面漆后不能安排任意黑色面漆，钻石白面漆前必须是极地白面漆。

1.2 零件摆放顺序

零件的前后摆放顺序为（门槛B），（门槛C），（门槛A，门槛D，后保A，门槛装饰条A），并且相同颜色的同种零件应尽量摆放在一起。

为避免门槛两端产生撞划伤，门槛B、门槛C不能与所有类型的雷达支架安排在一起喷涂。

2  问题描述与数学模型

2.1 问题描述

喷涂中用到的滑橇如图1所示。每个完整喷涂流程经过303个滑橇，一个滑橇喷涂工序节拍大概在1分钟，一个完整喷涂流程需要5.5个小时左右。

生产过程按照如图2所示不同颜色的不同配件具体生产需求量进行喷涂作业。因为在支架种类和支架数量一定的情况下，不同的生产排程方案导致成本和效率差异很大。为提高生产效率、降低生产成本，制定喷涂方案。

2.2 问题分析

每个完整喷涂流程提供滑撬数是确定的，而前后相邻两个滑橇上的配件喷涂不同面漆色，对应的喷枪更换涂料颜色则会增加作业时间。为减少作业时间，需制定换色次数最少的生产方案，并求出完成期望生产量喷涂的最少时间以及最小换色次数。

2.3 数学模型

数学建模己经广泛应用于自然科学与工程技术的各个领域，定量化研究己成为几乎所有学科发展的共同的理论和方法的基础。

2.3.1 模型假设

①生产线不会出现故障或者异常，且加工过程中没有停止，每一个完整生产流程完成后立即开始下一个完整生产流程，直到完成期望生产量;

②喷涂过程中，换色所用的滑橇喷涂时间与正常无异;

③生产出来的每个零件都是合格可用的。

2.3.2 模型建立

①构建生产时间与配件种类、配件喷涂颜色、配件喷涂数量、支架种类、支架数量等的数学关系;

②以颜色作为划分依据，将具有相同颜色的产品放在一起，统计数量信息并按降序排列;

③根据产品间的约束关系调整颜色与数量关系，将每种产品不能满足摆满一个滑撬的部分零件或者是一个完整流程中支架数不能满足的部分零件压入单调优先队列，按照降序顺序排列，生成新的加工顺序。

3  算法设计与模型求解

对于此模型，文章将生产效率最高这一优化目标转化成以换色次数最少为优化目标，设计出模型并利用贪心算法对其进行最优化分析求解。

3.1 算法设计

3.1.1 数据采集

为不将数据和配件信息分离，文章用浮点数类型的数组存储相同颜色的产品信息。对配件种类、配件喷涂颜色、支架种类进行对应标号。

3.1.2 算法流程

针对此多变量约束的数学动态规划模型，文章采用贪心算法，从局部出发寻找全局最优解[6][7][8]。

①将同种颜色产品放在同一数组，并调用二分思想的quicksort函数将所有元素按降序排列。

②以限制条件最多的门槛B和门槛C对产品间的约束进行划分。采用fit函数遍历数组中的每一个元素，获取该元素前两位小数存储的产品信息，通过位置的交换调整同种颜色中产品的先后顺序。

③调用other函数，遍历每种颜色对应的数组元素。获取该产品名称对应的编码、产品颜色、产品名称，输出滑撬上的产品信息。

3.2 模型结果

文章按照前文所述流程进行优化求解，最终输出cha=11，即最小换色次数为11次。同时输出的滑橇上產品信息和队列信息表明：完成期望生产量的喷涂最少需要进行八个完整喷涂流程，由喷涂工艺可知：一个完整喷涂流程需要5.5个小时。因此完成期望生产量的喷涂最少时间为44个小时。

4  总结

文章设定了指定的算法流程避免因贪心算法和动态规划的引入而造成的结果只是局部最优解的情况，并且利用一些特殊的数学方法，将文字信息转换成数字信息，清晰的描绘出满足汽车配件喷涂工艺条件的最优生产调配方式。

该方法思维复杂度低，模型简单高效，代码量小，稳定性好，能够对不同规模的短期最优策略问题在短时间内做出最符合实际的高效率策划方案，节省人力物力财力，达到最佳的收益需要。

但该方法缺乏真实性的严格证明，还有改进的空间。同时在实施过程中需要尽量满足模型的假定条件。总的来说这是一个很具有现实意义的探究，具有一定的推广应用价值。

参考文献：

[1]安琳，李艺铭.全球智能制造发展格局研判[J].机器人产业，2015（3）：34-41.

[2]刘勇，张亮.发展智能制造，促进兵器装备集团制造业转型升级—兵器装备集团智能制造技术与高端装备产业发展思考[J].兵工自动化，2017（1）：1-6.

[3]陆超.支持多品种小批量的复杂零件工序级生产排程方法研究[D].哈尔滨：哈尔滨理工大学，2013.

[4]陈梓祥.基于APS的制造业生产线调度系统设计与实现[D].济南：山东大学，2015.

[5]吴思旻.B汽车零件企业精益生产实践运用[D].成都：西南交通大学，2017.

[6]周亦军，李旻.标绘台标绘路径选择算法设计与实现[J].舰船电子工程，2012，32（5）：71-73.

[7]陆国锋.基于多约束多目标的旅游路线推荐及关键算法研究[D].长沙：国防科学技术大学，2013.

[8]吴军，李建，胡永泉.求解TSP问题的拟人算法[J].计算机系统应用，2011，20（4）：248-250，244.

作者简介：肖峰（1999-），男，重庆人，本科生，研究方向为机电一体化、智能机器人及其相关技术。