机械制图中已知切点的圆弧连接

严霞

摘要：在机械制图中，圆弧连接存在两种情况，第一种情况是已知连接弧半径，求作圆弧连接;第二种情况是已知一个切点，连接弧半径未知，求作圆弧连接。根据“已知线段”的不同，将第二种情况中的圆弧连接分为三种类型，分别对三种类型的圆弧连接作图方法和步骤进行了研究，归纳出已知切点时运用“三步法”作圆弧连接的方法，并举例应用。

关键词：圆弧连接;几何作图;已知切点

1  圆弧连接的另一种情况

在《机械制图》课程教学中，圆弧连接是几何作图部分的重点内容。圆弧连接存在两种情况，第一种情况是已知连接弧半径，求作圆弧连接。对于这一种情况，我们通常采用“求圆心、找切点、作圆弧”三步来作出连接弧，详细作图步骤可参见《机械制图》中几何作图（尺规作图）相关章节，这里不再赘述。第二种情况是已知一个切点（连接弧半径未知），求作圆弧连接。如图1所示，左上方连接圆？准14和圆弧R39的连接弧半径未知，但连接弧与圆？准14的公切线方向为已知，即已知一个切点，求作圆弧连接。这一种情况在企业零件测绘中也常会遇到，由于《机械制图》教材中没有对这一种情况中的圆弧连接作图方法和步骤进行详细介绍，同学们遇到这一类作图题目时往往束手无策，经过冥思苦想后，也只有屈指可数的几位同学能够作出正确解答。本文重点探索这一种情况中的圆弧连接，下文中的“圆弧连接”也仅指此情况中的圆弧连接。

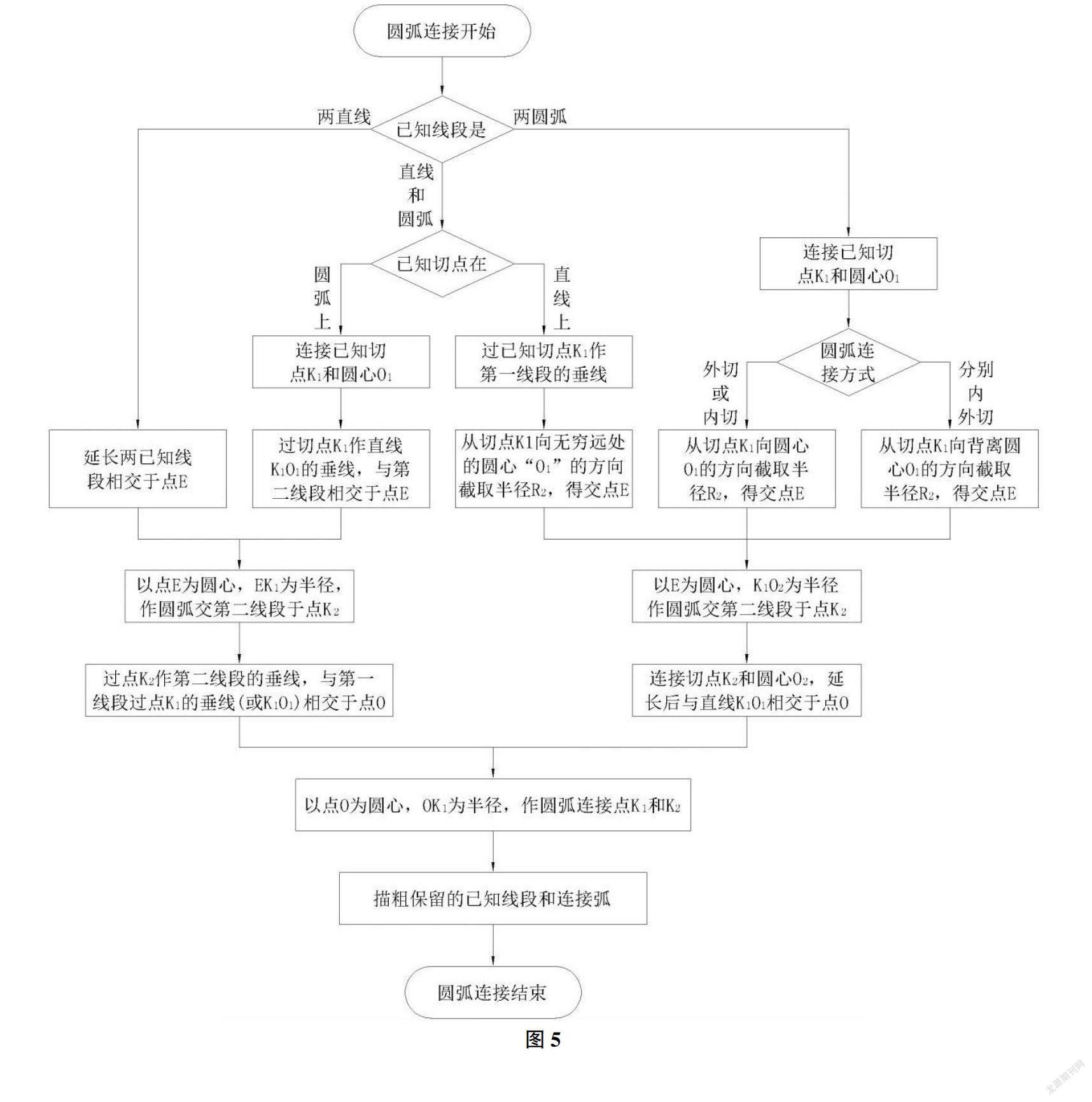
要作出图1中圆？准14和圆弧R39的连接弧，必须先求出连接弧的圆心。由于平面上的一个点是由两个坐标值确定的，即要知道两个条件才能求出一个点。本题中已知圆弧连接的一个切点，即只知道一个有效条件，所以不能直接求出连接弧的圆心，故采用“求圆心、找切点、作圆弧”三步不能作出连接弧。我们来探索采用“找切点、求圆心、作圆弧”这三步来作连接弧，这里的“找切点”是指找连接弧与另一已知线段（直线或圆弧）的切点。

圆弧连接中的“已知线段”既可以是像图1中的两圆弧，也可以是两直线，还可以是一直线和一圆弧。我们可以根据“已知线段”的不同，将圆弧连接分成三种类型。类型一：圆弧连接两相邻已知直线;类型二：圆弧连接两相邻已知圆弧;类型三：圆弧连接两相邻已知直线和圆弧。为便于讨论，我们将已知切点记作K1，另一切点记作K2;已知切点K1所在的线段称作第一线段，另一已知线段称作第二线段;第一线段如果是圆弧，其圆心记作O1，半径为R1;第二线段如果是圆弧，其圆心记作O2，半径为R2;连接弧的圆心记作O，半径为R。

2  圆弧连接两相邻已知直线

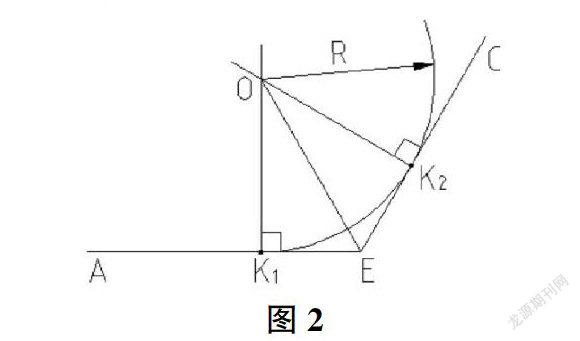
如图2所示，用一段圆弧光滑地连接两相邻直线AE和CE，点K1和点K2为切点（连接点）。分别过点K1作直线AE的垂线和过点K2作直线CE的垂线，两垂线相交于点O，点O即为连接弧的圆心，OK1=OK2=R;连接点O和点E，在Rt△OK1E和Rt△OK2E中，OE=OE，OK1=OK2，根据定理“斜边和一条直角边分别相等的两个直角三角形全等”可得Rt△OK1E≌Rt△OK2E，所以K1E=K2E，即圆弧连接两相邻已知直线时，两切点到两直线交点的距离相等。

如表1所示，已知两相邻直线AB和CD及直线AB上的一个切点（连接点）K1，求作圆弧连接。根据以上分析，我们归纳出圆弧连接两相邻已知直线的作图方法和步骤，说明如下：

①找切点。延长两已知直线相交于点E，以点E为圆心，EK1为半径，作圆弧交第二线段于点K2，点K2即为所求另一切点。②求圆心。分别过点K1和K2，作直线AB和CD的垂线相交于点O，点O即为连接圆弧的圆心。③作圆弧并描粗。以点O为圆心，OK1为半径，作圆弧连接点K1和K2，描粗保留的已知线段和连接弧，圆弧连接完成。

3  圆弧连接两相邻已知圆弧

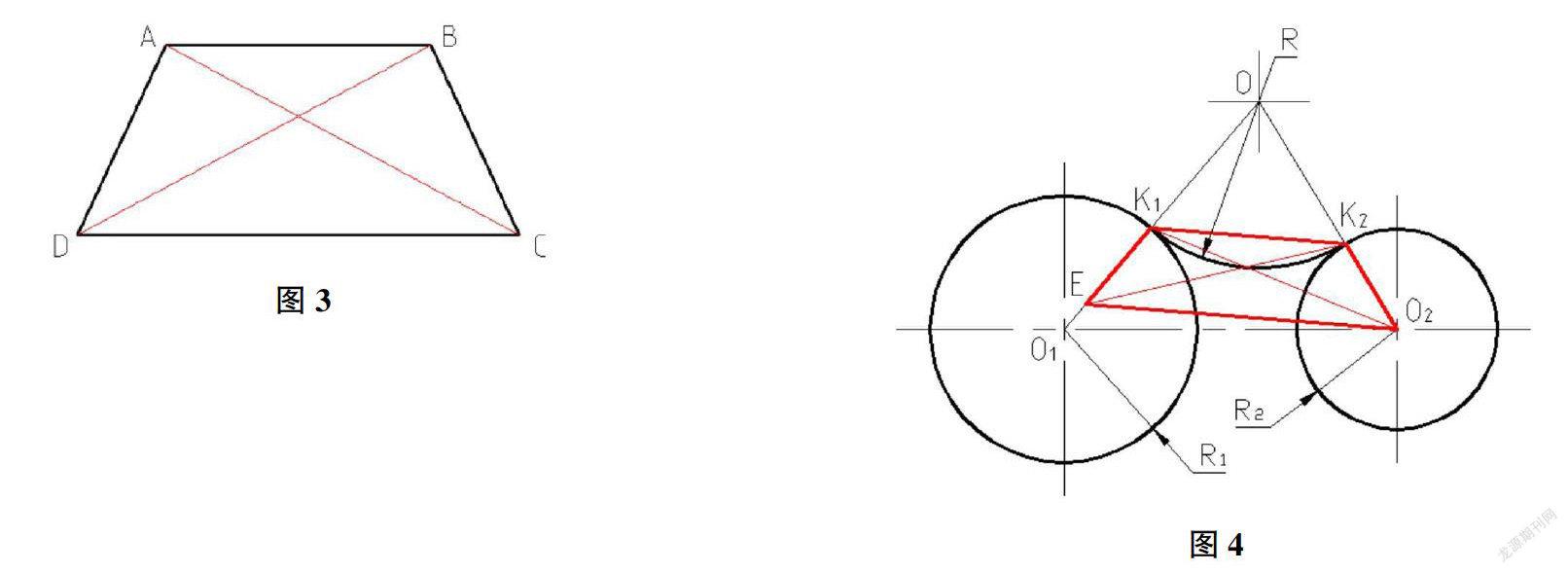
我们先来看等腰梯形的一个性质：等腰梯形的对角线相等。（图3）

如图3所示，等腰梯形ABCD的对角线分别为AC和BD，在△ADC和△BCD中，AD=BC，∠ADC=∠BCD，DC=CD，根据基本事实“两边及其夹角分别相等的两个三角形全等”可得△ADC≌△BCD，所以AC=BD，即等腰梯形的对角线相等。圆弧连接两相邻已知圆弧中就隐藏着一个等腰梯形，而“找切点”的关键就是找到这个等腰梯形。（图4）

如图4所示，半径为R的圆弧光滑地连接着半径分别为R1和R2的两个圆。两个圆（圆弧）相切，切点必在两个圆心的连线上，我们把这条直线称作连心线。连接圆心O和O1，与半径为R1的圆弧相交于点K1，连接圓心O和O2，与半径为R2的圆弧相交于点K2，点K1和点K2即为切点。在连心线OO1上从切点K1向圆心O1的方向截取另一圆弧的半径R2，与连心线OO1相交于点E，即K1E=K2O2=R2。连接点K1和点K2，连接点E和O2，在等腰△K1OK2中，∠OK1K2=（180°-∠O）/2，在等腰△EOO2中，∠OEO2=（180°-∠O）/2，所以∠OK1K2=∠OEO2，根据基本事实“同位角相等，两直线平行”可得K1K2∥EO2，所以四边形K1EO2K2便是隐藏在圆弧连接两相邻已知圆弧中的一个等腰梯形，其对角线K1O2=K2E。当然，我们在作圆弧连接时，并不需要将这个等腰梯形的四条边全部作出来。

根据以上分析，我们归纳出圆弧连接两相邻已知圆弧的作图方法和步骤，如表2所示，说明如下：

①找切点。连接已知切点K1及相应的圆心O1，当连接弧与两已知圆弧外切或内切时，从切点K1向圆心O1的方向截取半径R2，与直线K1O1相交于点E;当连接弧与两已知圆弧分别内外切时，从切点K1向背离圆心O1的方向截取半径R2，与直线K1O1相交于点E。以点E为圆心，以已知切点K1至圆心O2的距离为半径，作圆弧交第二线段于点K2，点K2即为所求另一切点。

②求圆心。连接切点K2和圆心O2，延长后与直线K1O1相交于点O，点O即为连接圆弧的圆心。

③作圆弧并描粗。以点O为圆心，以线段OK1为半径，作圆弧连接点K1和K2，描粗保留的已知线段和连接弧，圆弧连接完成。

4  圆弧连接两相邻已知直线和圆弧

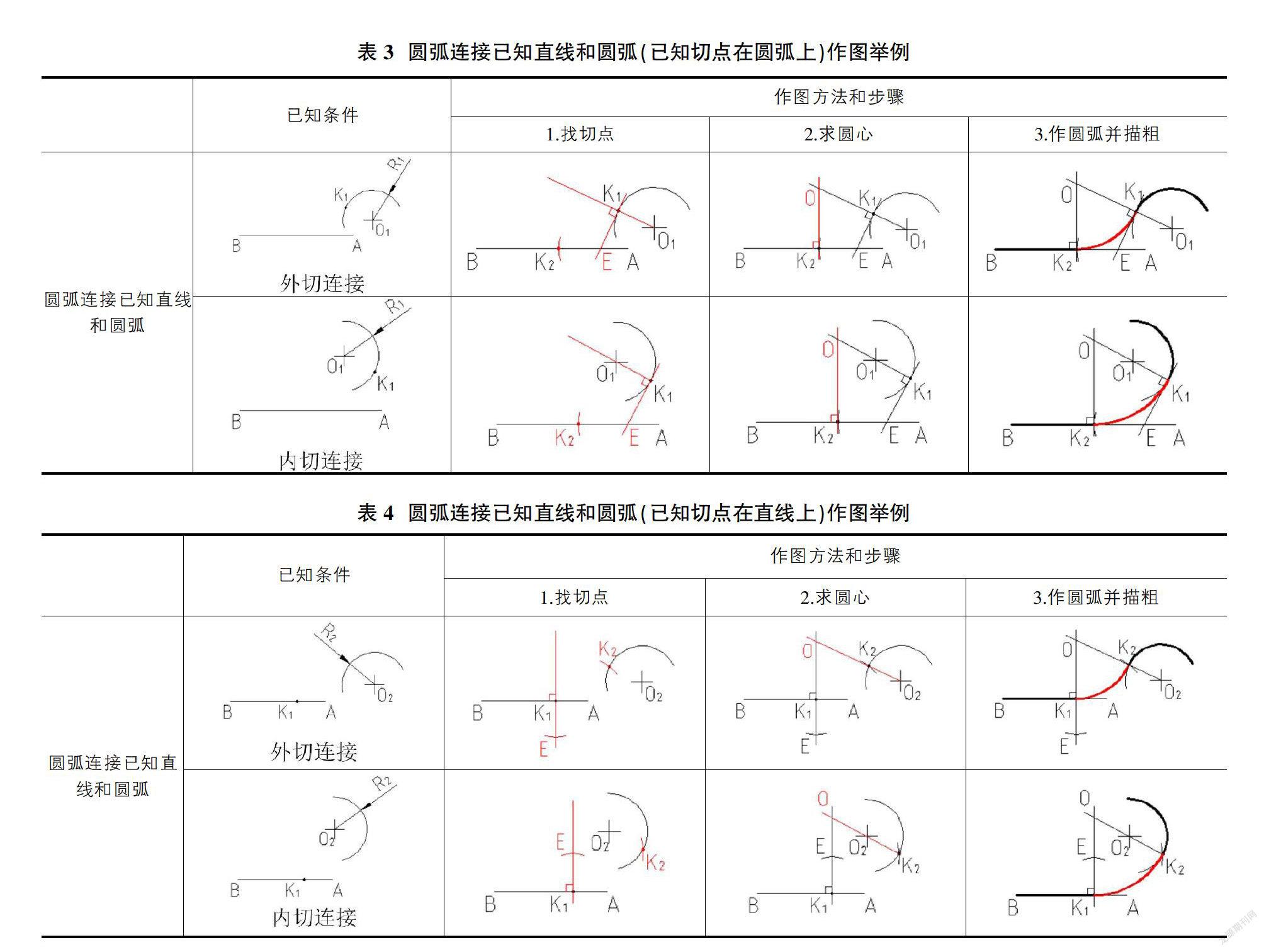
用一段圆弧光滑地连接两相邻已知直线和圆弧，当已知切点在圆弧上时，作图方法和步骤如表3所示。在第一步“找切点”时，先连接已知切点K1和圆心O1，然后过已知切点K1作直线K1O1的垂线（已知圆弧的切线）与已知直线AB相交于点E，从而将此类问题转化为圆弧连接两相邻已知直线的问题，后续作图方法和步骤亦与上文中“圆弧连接两相邻已知直线”的作图方法和步骤相同。

用一段圆弧来光滑地连接两相邻已知直线和圆弧，当已知切点在直线上时，如果将直线理解为一个直径无穷大的圆，此类问题就可以转化为圆弧连接两相邻已知圆弧的问题了，作图方法和步骤如表4所示。由于这里的“圆弧”直径无穷大，所以在第一步“找切点”时，将原来的“先连接已知切点K1及相应的圆心O1”改成“过已知切点K1作已知直线AB的垂线”就可以了，后续作图方法和步骤亦与上文中“圆弧外切或内切连接两已知圆弧”的作图方法和步骤相同。

5  总结及实例

上面介绍的已知一个切点时三种不同类型的圆弧连接作图方法，由于都是按照“找切点、求圆心、作圆弧”这三步来完成作图的，我们将其称作“三步法”作圆弧连接。根据以上分析，我们总结出“三步法”作圆弧连接的方法和步骤，其流程图如图5所示。

下面我们应用“三步法”绘制图1中连接圆？准14和圆弧R39的连接弧（在绘制连接弧前，已完成图1中其他线条的绘制，如图6所示）。

连接弧与两已知圆弧都是外切，属于“圆弧外切连接两已知圆弧”的类型，作图方法和步骤如图7所示，说明如下：

①找切点。从已知切点K1向圆心O1的方向截取另一已知圆弧的半径39mm，与直线K1O1相交于点E;以点E为圆心，以已知切点K1至另一已知圆弧的圆心O2之间的距离为半径，作圆弧交另一已知圆弧于点K2，点K2即为所求另一切点。

②求圆心。连接切点K2和圆心O2，与直线K1O1相交于点O，点O即为连接圆弧的圆心。

③作圆弧并描粗。以点O为圆心，以线段OK1为半径，作圆弧连接点K1和K2，描粗保留的已知线段和连接弧，圆弧连接完成。

同学们在学习了“三步法”作已知切点的圆弧连接后，遇到类似的题目再也不会抓耳挠腮、不知所措了，只要根據已知条件先确定一个切点（连接点）和连接类型，然后按照相应类型的“找切点、求圆心、作圆弧”这三步就可以轻而易举地完成作图了。经过教学实践，在对学生进行以上作图方法的详细介绍后，能够解决此类作图问题的学生人数大幅提高，约85%的同学经过简单思考或提醒后能够作出正确解答，教学质量显著提高。

参考文献：

[1]全国技术产品文件标准化技术委员会，中国标准出版社.技术产品文件标准汇编：机械制图卷[G].北京：中国标准出版社，2007.

[2]钱可强.机械制图[M].三版.北京：高等教育出版社，2011.

[3]柳燕君，应龙泉，潘陆桃.机械制图[M].北京：高等教育出版社，2010.