基于模糊自抗扰控制在电动汽车PMSM位置驱动系统研究

李晶

摘要：为实现电动汽车用PMSM转速快速响应和强鲁棒性，本文提出一种基于模糊自抗扰的电动汽车PMSM驱动控制系统，将模糊控制与自抗扰控制结合，将位置反馈作为控制器反馈信号，结合自抗扰控制器中状态变量估计和微分之间的误差，建立误差的模糊规则控制表，进行去模糊化之后得到误差精准的控制量，并通过对非线性误差状态反馈控制率的误差比例系数、微分系数、积分系数进行自适应调节，实现对扰动量的补偿控制，增强电动汽车PMSM驱动系统的抗扰动能力。

关键词：PMSM;模糊自抗扰控制;非线性误差状态反馈控制率

1  概述

电动汽车是将电能作为能量源，通过能量转换变成由全部或部分电动机驱动行驶的车辆。电动汽车驱动系统即电驱动系统既是关键技术又是共性技术。与普通的工业用电机控制系统不同，对整个系统的可靠性、耐久性、安全性提出了更高的要求。永磁同步电机（PMSM）目前已经成为驱动电机发展的主要趋势。为了提高电机的动态性能和鲁棒性，一些先进的控制方法也随之应用到了电动汽车用永磁同步电机控制上。本文主要提出的是基于自抗扰控制参数调整已达到有效抑制扰动，提高电机控制性能的方法。PMSM本身是一个非常复杂的非线性控制对象，具有变量多、耦合性强等特点，在工业生产过程中，对其控制常常会出现滞后、时变等问题，因此单独使用一种控制方法很难达到工业生产要求，因此本文将模糊控制与自抗扰控制策略相结合，突破电机控制过程中需要划分线性与非线性、时变与非时变、确定与不确定等探究模式的局限，进一步提高电动汽车PMSM驱动系统的动、静态特性。使之具有较强的鲁棒性和抗扰动特性。

2  设计自抗扰控制器

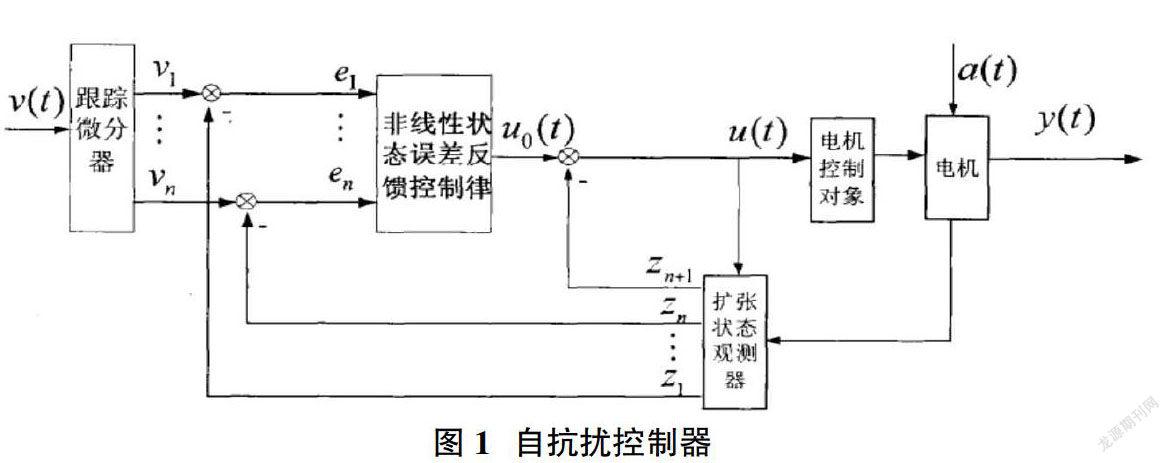
自抗扰控制器包含跟踪微分器（Tracking-Differentiator，TD）、扩张状态观测器（Exrended State Observer，ESO）和非线性误差反馈控制率（Nonlinear State Error Feedback，NLSEF）三部分组成，如图1所示。

从图1中我们可以看到扩张状态观测器是本控制系统的核心部分，通过观测器对输入输出进行扰动观测，发现异常可以直接进行补偿。同时不用系统的模型信息是否已知，都可以对其进行内扰观测并补偿直至扰动消除，这就是自抗扰控制的优势所在，而且其对扰动的观测和补偿是通过串联积分器来实现的这样使整个控制系统更容易控制。

2.1 自抗扰控制器的算法

2.1.1 跟踪微分器

2.1.2 扩张状态观测器

2.1.3 非线性状态反馈控制律

2.2 基于模糊自抗扰控制的电动汽车用PMSM驱动系统

为提高电动汽车PMSM驱动系统的抗扰动性减小外部扰动对其的影响提升系统的自适应能力，本文将模糊控制与自抗扰控制器相结合引入到电动汽车PMSM驱动系统中，具体实现过程如下：

首先根据TD产生的微分与ESO的状态变量之间的误差，得到误差比例系数，建立误差比例系数、微分系数和积分系数的模糊控制规则，去模糊化之后得到精准的控制量，以实现NLSEF的参数自适应调节。最后按照控制框图NLSEF和ESO的扰动补偿一起作为控制量，以此来实现对电动汽车PMSM驱动电机的最优控制。改进之后自抗扰控制器能够提升PMSM的位置精度，同时系统抗扰能力也明显增强。通过仿真实验和结果分析，改进后的模糊自抗扰控制器具有响应速度快、无超调、稳态精度高、对负载及系统扰动鲁棒性更强的特点。

对于模糊自抗扰位置伺服系统而言，只需要给定位置误差以及位值误差变化率，就能实现利用模糊控制对NLSEF控制参数的自整定，最终实现参数跟踪实际位置误差进行自适应调整，有利于提高位置精度。从上述算法及图示中我们可以知道，自抗扰控制器参数比较多，每一个部分都有其自己的参数需要整定，因此我们需要把跟踪微分器、扩张状态观测器和非线性反馈控制律中涉及到参数分开整定，这样才能够得到完整的自抗扰控制器整定参数。其中跟踪微分器参数基本上可以固定化，扩张状态观测器参数与扰动幅值成正比，非线性反馈控制率参数整定是难度最大的，本文采用模糊控制理论对非线性组合部分参数进行整定，将误差e和误差变化率ec作为控制器的输入，利用模糊规则对参数βi进行修改，从而实现其整定。假设误差e及误差变化率ec和βi在模糊集的论域为（-3，3）。隶属度函数为灵敏度较高的三角函数。控制规则如下：

①对于位置误差e较大的情况，应当适当增加比例增益的值，保障系统的快速跟踪能力，使系统反应迅速。对于位置误差e较小的情况下，可以适当增加积分增益和比例增益的值，使得系统的抗扰动性能增强，同时适当增加微分增益的值一直振荡的发生。

②对于位置误差率ec较大的情况则需要减小微分增益和比例增益增加积分增益保障系统运行的稳定。另外在位置误差变化率ec较小的情况下适当增加微分增益同时针对实际工作情况调整比例增益和积分增益。综上所述根据控制规则得到相应的控制规则表。

2.3 电动汽车PMSM驱动系统

3  结论

其实结合了模糊控制的自抗扰控制器即（Fuzzy-ADRC）与原来的自抗扰控制器即ADRC相比，仅仅是对其组成部分的非线性反馈控制率（NLSEF）部分进行调整，这样就使整个控制器Fuzzy-ADRC的参数达到最优控制效果，从而提高了PMSM伺服位置控制精度。实验结果显示结论是成立的，这也为Fuzzy-ADRC应用在更多的PMSM伺服控制系统中打下良好的基础，使其能在工程实际应用中取代PID控制器。

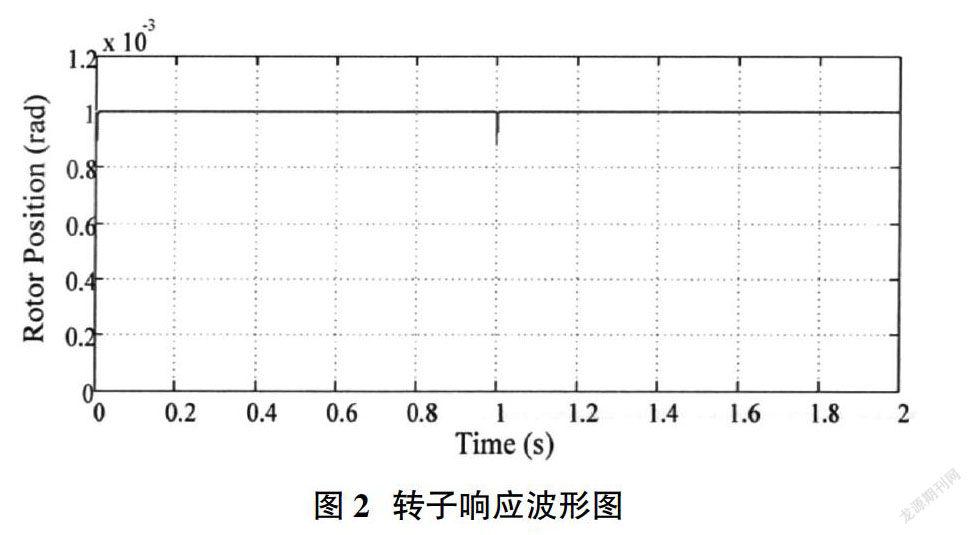
试验中设计的控制对象电动汽车的PMSM相关参数如下：额定功率为1.85kW，额定转速为6000r/min，定子绕组Rs=1.8Ω，直轴、交轴自感Ld=Lq=7.3mH，转动惯量J=0.0013kg·m2，极对数np=2，额定转速Te=3N·M，转子磁链ψf=0.248Wb，额定频率fN=200Hz。给定位置为0.001rad，空载启动电机，在1s时施加1牛米的扰动进行干扰，得到仿真图形如图2，由此可知Fuzzy-ADRC能够较快的对扰动进行响应，确保PMSM位置伺服系统的自抗扰效果良好。

参考文献：

[1]Paolo Lino， Guido Maione， Silvio Stasi， Fabrizio Padula，Antonio Visioli. Synthesis of Fractional-order PI Controllers and Fractional-order Filters for Industrial Electrical Drives[J]. IEEE/CAA Journal of Automatica Sinica， 2017， 4（01）：58-69.

[2]黃庆.交流永磁电机伺服系统复合自抗扰控制策略研究[D].湖南大学，2014.

[3]高志强.自抗扰控制思想探究[J].控制理论与应用，2013，30（12）：1498-1510.

[4]单亚运.基于模糊自适应分数阶PID伺服控制系统研究与设计[D].江苏科技大学，2018.