某轨道车辆车轮疲劳强度分析

王宗正

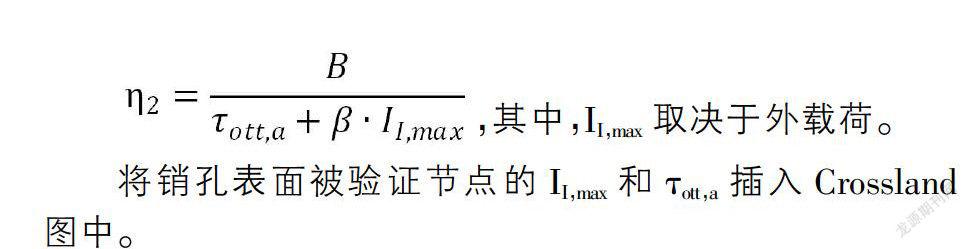
摘要：采用ABAQUS 2016软件对某轨道车辆车轮进行三维有限元分析，基于EN 13749 及 UIC 510-5标准计算了车轮在直线、曲线和道岔工况下，不同载荷加载平面下的应力，组合最大主应力投影准则与Crossland多轴疲劳准则对车轮辐板与辐板孔的疲劳强度进行了分析，计算结果说明，这种组合疲劳评定准则的评价结果可以较好的评估车轮抗疲劳性能。

Abstract： In this dissertation， a rail vehicle wheel is chosen as the research subject. Based on the three-dimensional finite element method we analyze the wheel in Abaqus 2016. Based on three conditions of straight line， curve and turnout in EN 13749 and UIC 510-5 standard， calculate the stress of the wheel under different loading planes. Combined with the maximum principal stress projection criterion and the Crossland multi axle fatigue criterion， the fatigue strength is analyzed for both the wheel web and the web pin hole. The calculation results show that this combined fatigue evaluation criterion can evaluate the wheel fatigue performance very well.

關键词：车轮;疲劳强度;最大主应力投影;多轴疲劳

Key words： wheel;fatigue strength;maximum principal stress projection;multiaxial fatigue

中图分类号：U270.35                                    文献标识码：A                                文章编号：1674-957X（2020）22-0048-03

0  引言

车轮是转向架的关键部件之一，其安全性对于列车的安全运营至关重要[1][2]。车轮的运营工况复杂，工作环境恶劣，容易发生疲劳破坏。随着列车运营速度的提升及载重量的增加，车轮疲劳安全问题越来越重要，在车轮投入运用前，须评价其疲劳性能，以确保其服役可靠性。

现有的轨道车辆车轮疲劳评定准则主要包括单轴疲劳评定准则与多轴疲劳评定准则，其中单轴疲劳是指材料或零部件在单向循环载荷作用下产生的失效现象，多轴疲劳是指材料或零部件在复杂多维交变应力周期性性变化下造成的疲劳失效破坏。针对车轮辐板及辐板销孔的结构及受载特性，本文采用了单轴疲劳准则最大主应力投影准则评定车轮辐板疲劳强度，采用了Crossland多轴疲劳准则评定辐板销孔疲劳性能[3][4]。

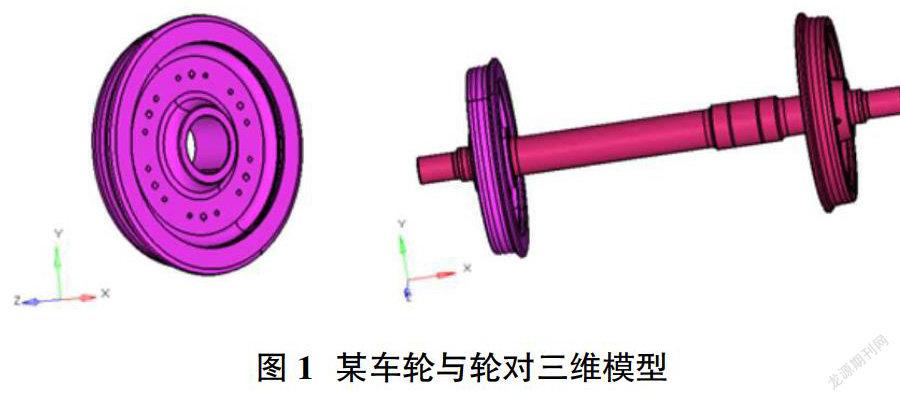
1  车轮概况

某轨道车轮由CL60钢整体轧制而成，弹性模量为210GMPa，泊松比为0.3，屈服极限为355MPa，疲劳极限为车轮直径为840mm，轴重为15t，轮轴配合最大过盈量为0.277mm，设计最高运营速度100km/h。由CL60钢锻造而成，von Mises 屈服强度为355MPa，疲劳极限为180MPa，弯曲疲劳极限为254MPa，扭转疲劳极限为177.5MPa。

2  有限元模型

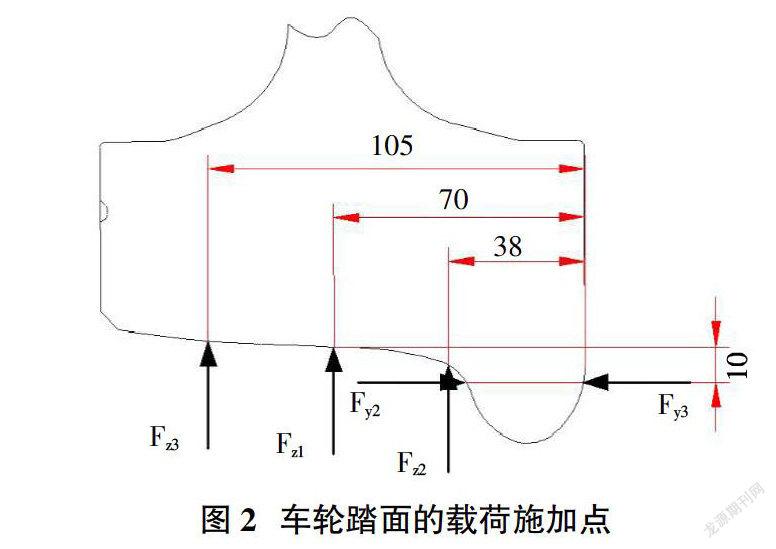
在车轮静强度验证和疲劳强度验证时必须采用三维模型，计算中选取整个车轮和车轴的一部分作为计算对象，整个模型均采用ABAQUS软件中的实体单元C3D8R，模型共有145524个单元和138684个节点，应力集中部位单元尺寸为5.06mm，车轮与车轴采用过盈配合，载荷以集中力的方式施加在图2所示的车轮几何外形面上，施加绕车轮轴线的角速度以考虑离心力作用。

2.1 加载与约束

车轴模型的两端施加径向和周向约束，一端施加轴向约束，有限元模型与约束施加位置见图3。

2.2 计算工况

依据EN13979-1：2003《铁路应用-轮对和转向架-整体车轮-技术认证程序第1部分：锻造和轧制车轮》和UIC 510-5 OR《整体车轮的技术认证-标准EN13979-1第2版的应用文件》中所给的载荷组合和载荷施加点进行强度计算;[5][6]载荷计算与工况选取如下：

3  评定方法

3.1 最大主应力投影准则

首先根据计算结果选出三种工况中给定节点的最大σi（主应力编号i=1，2，3）值，作为σimax，计算出σi的方向余弦向量（nσimaxx，nσimaxy，nσimaxz），应用方向余弦向量与此节点在其余两个工况下的应力张量矩阵，计算得到σimin，应用σmax与σmin计算得出平均应力和应力幅值，对每个考察节点，表1总结了5个应力循环。

3.2 Crossland多轴疲劳准则

对于车轮辐板销孔的疲劳验证，采用Crossland多轴疲劳标准来考虑孔表面的多轴应力状态。Crossland多轴疲劳标准采用最大应力分量，并且认为安全性随变量？子ott，a（动态八面体剪应力）而变。

4  疲劳强度计算结果

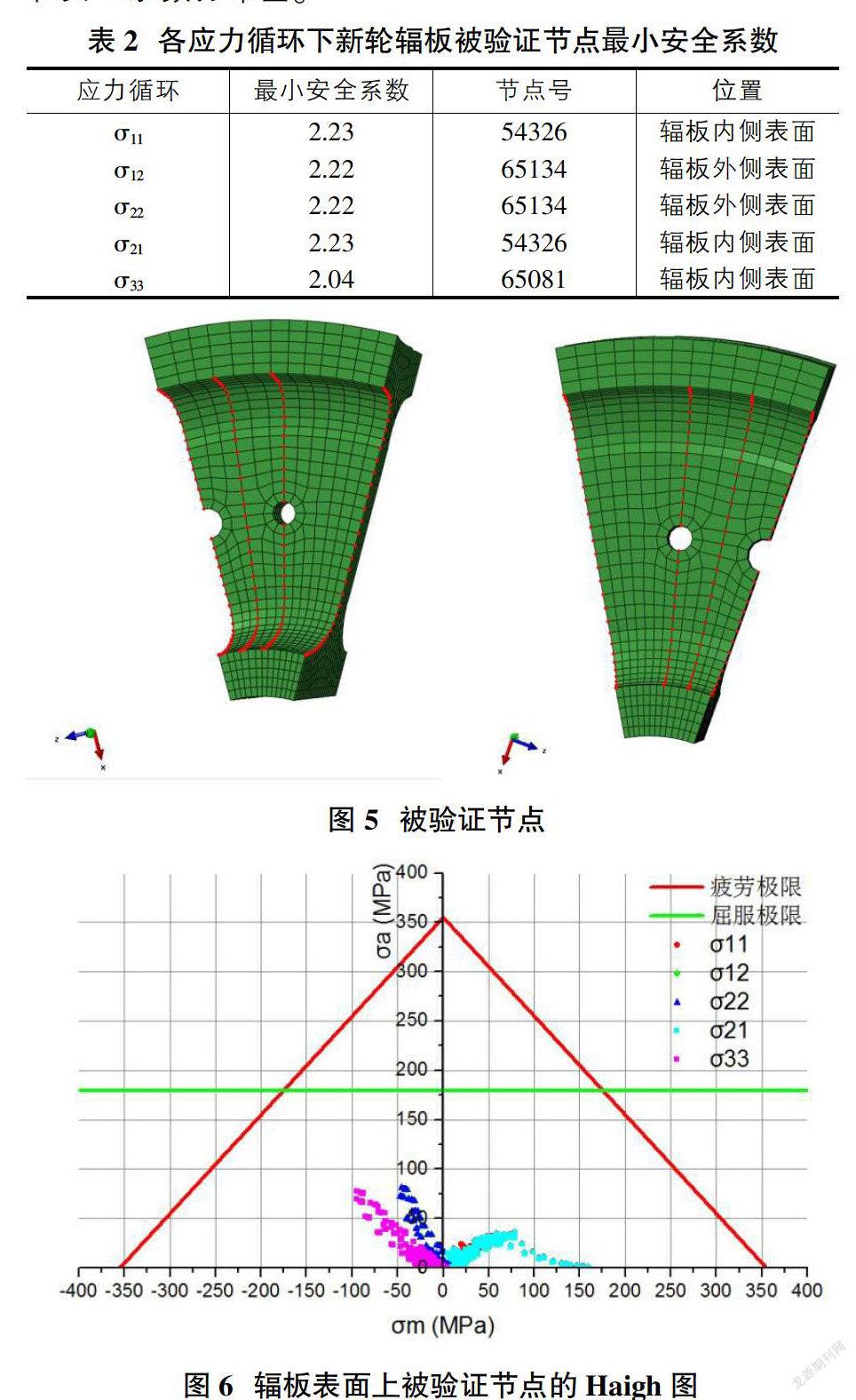
4.1 车轮辐板疲劳强度计算结果

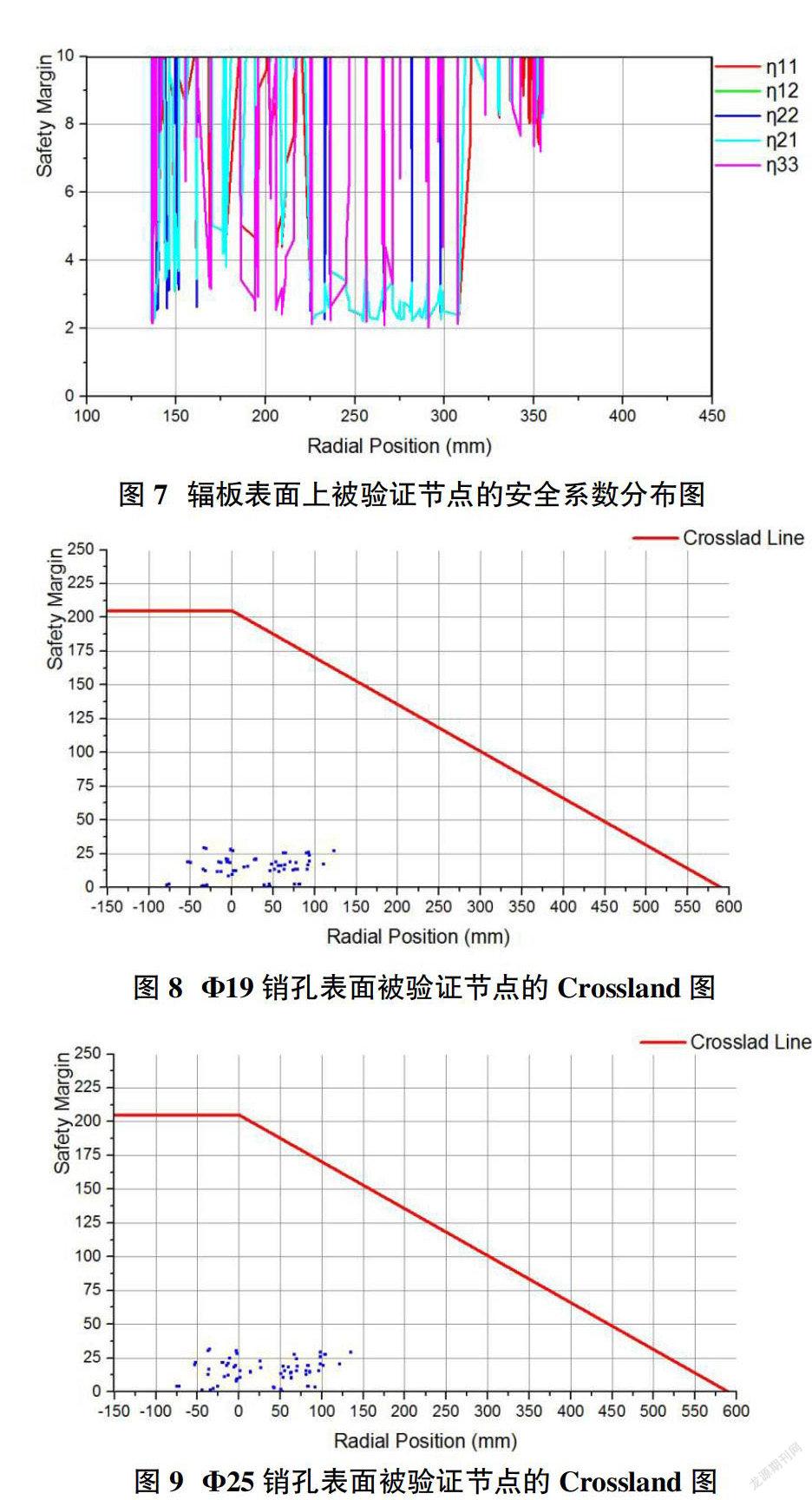
依据3.1节所述的方法对车轮辐板的疲劳强度进行分析，图5为进行疲劳强度验证的节点，各应力循环下新轮辐板被验证节点最小安全系数见表2，新轮辐板被验证节点最小安全系数为1.99，位于新轮辐板外侧表面，节点号为60928，出现在σ12、σ22应力循环中，图6为安全系数小于2的节点在车轮上的位置，均出现在σ12应力循环和σ22应力循环中，图7为被验证节点对应的Haigh曲线图和安全系数分布图。

4.2 辐板销孔疲劳强度计算结果

依据3.2节所述的方法对车轮辐板的疲劳强度进行分析，图8、图9为对新轮辐板销孔表面被驗证节点的Crossland图，辐板Φ19销孔表面节点安全系数η1最小值为6.11，安全系数η2最小值为2.97;辐板Φ25销孔表面节点安全系数η1最小值为5.47，安全系数η2最小值为2.71。

5  结论

采用了单轴疲劳准则最大主应力投影准则评定车轮辐板疲劳强度，采用了Crossland多轴疲劳准则评定辐板销孔疲劳性能：①辐板被验证节点最小安全系数为2.04，位于新轮辐板内侧表面，节点号为65081，出现在σ33应力循环中。②辐板Φ19销孔表面节点安全系数η1最小值为6.11，安全系数η2最小值为2.97;辐板Φ25销孔表面节点安全系数η1最小值为5.47，安全系数η2最小值为2.71。

参考文献：

[1]张澎湃.基于主应力法和修正的Crossland疲劳准则的动车组车轮强度评定方法[J].中国铁道科学，2014，35（2）：52-57.

[2]唐道武.机车车轮多轴疲劳强度安全评定的研究[J].内燃机车，2008，7：10-13.

[3]王悦东.基于改进的Goodman曲线的车轮疲劳强度评估方法研究[J].铁道科学与工程学报，2017，14（4）：827-832.

[4]王悦东.单轴和多轴疲劳准则下的车轮疲劳强度分析[J]. 大连交通大学学报，2016，37（2）：47-52.

[5]International Union of Railways， UIC 510-5-2007 Technical Approval of Monobloc Wheels [S]. Paris： UIC，2007.

[6]BS EN 13979-1，Railway Application-Wheelsets and Bogies-Mnobloc Wheels-Technical Approval Procedure-Part1：Forged and Rolled Wheels[S].BSI，2003.

[7]徐灏.疲劳强度[M].北京：高等教育出版社，1988.