传染病背后的数学模型

张成

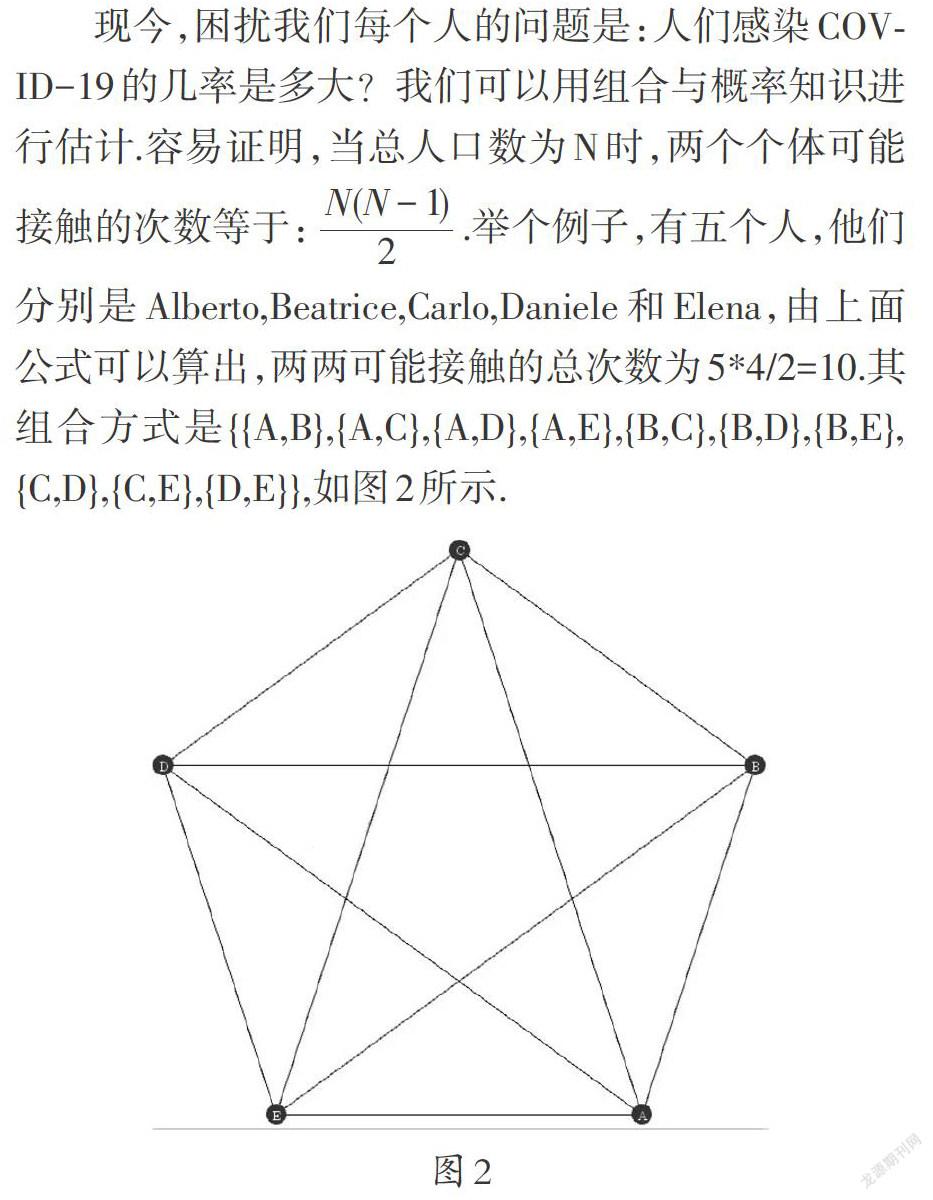
由新冠病毒COVID-19引起的肺炎疫情在全球不断蔓延，所有的媒体都在持续报道，我们的生活也因为各种防疫政策和措施受到了很大的影响。人们都在谈论与疫情相关的内容，如预防新冠病毒的方法、有关新冠病毒研究的最新消息、每天确诊病人及死亡病人的数量等，而科学家们则在尝试预测疫情的演变趋势。

在对人类历史上出现的传染病进行分析和研究的基础上，许多学者已经研究出一些可以描述和预测这种病毒的传播趋势与动向的数学模型。这些模型又是如何建立的呢？主要的方法是通过计算大规模收集来的相关数据，对相应机制作出假设，然后再通过观察，对其进行修改、完善，从而得出最终的数学模型。尤其值得说明的是，一个好的模型须最大程度地减小模型估计值与实际值之间的差距，这样才能重现一个地区疾病病例的时间序列。

历史上，法国数学家丹尼尔·伯努利（DanielBer-noull，1700年-1782年）是最早尝试进行这项数学研究的人，他曾尝试对天花的传播作出定量描述。大约在十八世纪中叶，天花是一种具极强传染性的疾病，其主要通过空气传播。当时，它几乎是全世界最严重的区域传染病。在欧洲，它曾是主要的致死原因，每年约有40万人因染此病而死去。在1760年的论文《天花死亡率新分析以及对预防性接种疫苗的优势研究》里，伯努利提出了一个关于感染人数呈指数增长的数学模型，并在此基础上证明了采用接种疫苗的方式来预防这种疾病是非常有效的。伯努利的研究非常具有前瞻陛，其发表的时间比爱德华·詹纳（EdwardJenner）发明预防天花病的方法——接种疫苗法，还要早四十年。1927年，苏格兰科学家马克（Kermack，1898年-1970年）和麦肯德里克（McKendrick，1876年-1943年）合写了一篇文章“对流行病数学理论的贡献”，并提出了SIR模型。在该文中，两位科学家将感染人群分成了三种类型：

1.易感染人群（susceptible，用S表示）：指那些尚未感染但很有可能被感染的人群;

2.感染人群（infectious，用I表示）：指那些已经感染且具有传染性的人群;

3.治愈人群（recovered，用R表示）：指那些已感染但不再具有传染性的人群。不再具有传染性是因为被治愈或者已去世，或者被隔离。

馬克和麦肯德里克意识到，在大多数流行病中，一个人只能从类型1过渡到类型2，或者从类型2过渡到类型3，而不可能从类型3返回至类型2（假设被治愈的人具有了对该疾病的免疫力）。这两位科学家建立的这个特定模型是微分方程组，该微分方程组能够表示出上述三种流行病学类型的数量S（t）、I（t）、R（t）随时间的变化趋势。

阿尔弗雷德·洛特卡（AlfredLotka）和维托·沃尔泰拉（vitoVolterra）曾利用微分方程组来描述一个生态系统的动态变换情况。在他们提出了这个著名的模型之后不久，马克和麦肯德里克也利用微分方程组，建立了一个关于三类流行病感染人群S、I和R的数学模型，被称为SIR模型。如果该疾病不涉及免疫接种（譬如感冒），就没有R类型的人群，那么探讨的就是SI模型。利用SIR模型，我们能预测流行病的演变趋势，并估计出s、I、R三类人群的人口比例。sIR模型是一种理想型的数学模型，所以它要求所有的数据必须是在理想的情况下得出的，具体如下：

1.在流行病期间，没有新增人口;

2.在流行病期间，死亡的主要原因是该流行病本身;

3.人口是被隔离的，即对于外部来说没有入流量与出流量;

4.该疾病没有潜伏期;

5.治愈康复后立即获得免疫力;

6.无论感染后经过多长时间，疾病的传染强度相同。

显然，这些假设与现实实际情况相比太过简单。比方说，新冠病毒的潜伏期有14天，而且，治愈后的免疫力也并没有被证实，所以第一种假设与第二种假设是不成立的。从另一方面讲，在建模的过程中，人们会很自然地着眼于现实现象中的关键要素，而忽略了一些被认为是次要的细节，比如在确定弹道轨迹的时候忽略与空气间的摩擦阻力，因为这对计算来说不是很重要。

在该模型下，这三类人群的数量是如何随时间变化的呢？怎样用数学语言去描述S（t），I（t）和R（t）这三个函数的变化趋势呢？为此，我们需要先分析前面提到的类型转变过程背后的机制。比如，个体从s类型变为I类型意味着什么？很简单，这个人被感染了，从而具有传染性。这个过程是感染者与易感染者之间产生了接触，把病毒传染给了后者。

在疫情开始时，易感染人群（即尚未感染的人群）的数量将会逐渐减少，而感染人群的数量将会因被传染而增长。随着感染人数的增加，一个易感染个体被感染的可能性将会更大，因此，感染人群的增长率将会从一开始就趋于加速（尽管伯努利从不同的假设着手分析，却也预估到了指数变化的趋势）。但是，在某些时候，一些个体将会开始从I类型转变到R类型，因为，他们有可能治愈康复了，或者死亡了，也或者被隔离了。从疫情爆发开始，只要感染者的数量多于移出者的数量（移出者数量=治愈数+死亡数+被隔离数），该流行病的走势将会处于上升阶段，但是，当移出者数量开始占上风之后，就又会处于下降阶段。有一个事实是确定的：易感染人群的数量总是在减少，而移出者数量总是在增加。

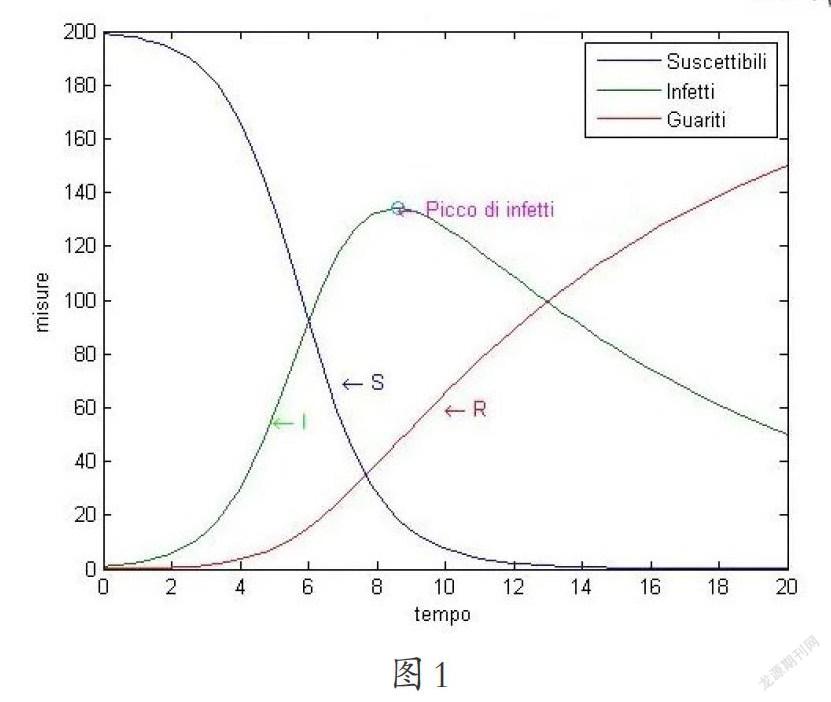
图1是一个用SIR呈现的一种流行病可能出现的趋势图。通过观察该图，你会发现，当感染者的数量达到一个峰值之后就会逐渐下降。这是因为，易感染者的数量总是在减少，而治愈者的数量总是在增加。

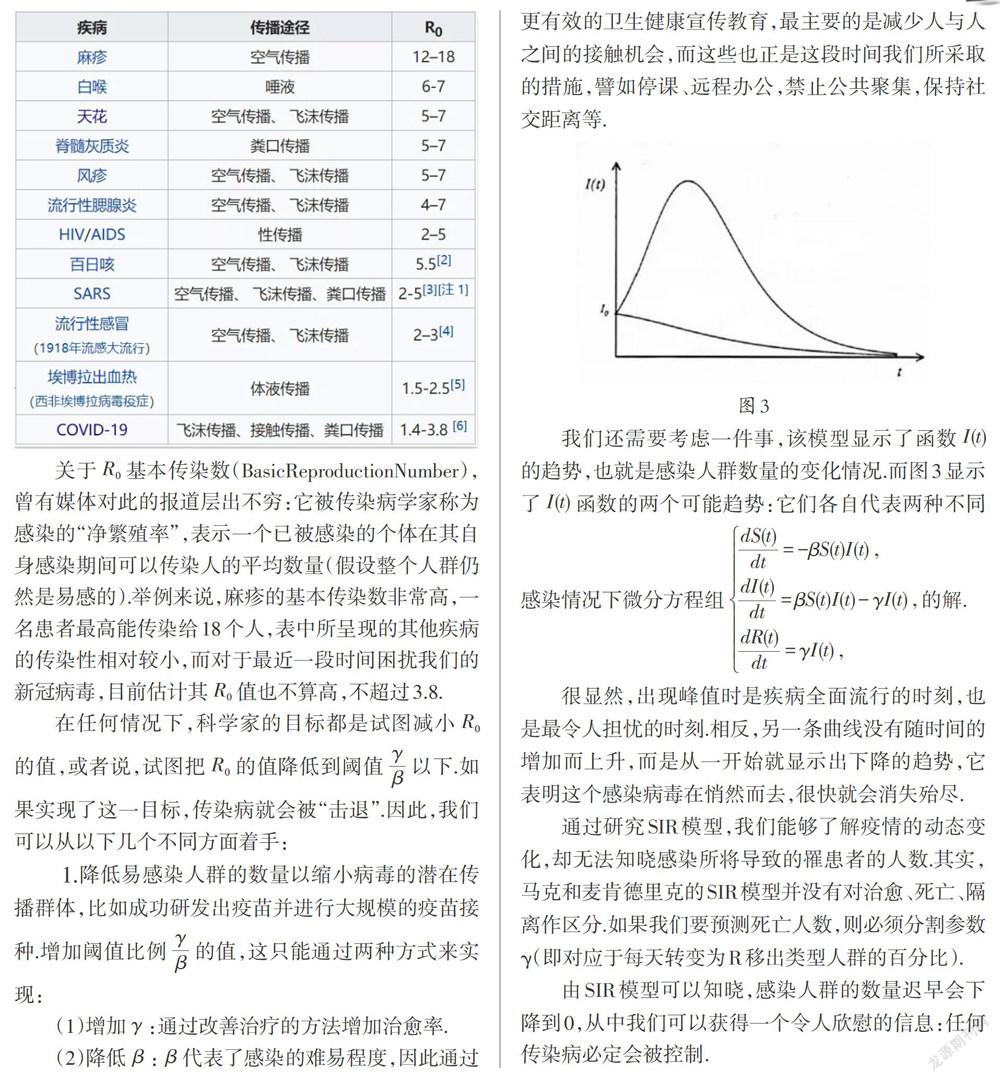
很显然，出现峰值时是疾病全面流行的时刻，也是最令人担忧的时刻。相反，另一条曲线没有随时间的增加而上升，而是从一开始就显示出下降的趋势，它表明这个感染病毒在悄然而去，很快就会消失殆尽。

通过研究SIR模型，我们能够了解疫情的动态变化，却无法知晓感染所将导致的罹患者的人数。其实，马克和麦肯德里克的SIR模型并没有对治愈、死亡、隔离作区分。如果我们要预测死亡人数，则必须分割参数y（即对应于每天转变为R移出类型人群的百分比）。

由SIR模型可以知晓，感染人群的数量迟早会下降到0，从中我们可以获得一个令人欣慰的信息：任何传染病必定会被控制。