基于分形理论的珠江口海岸线变迁分析
岳文,颜彬,张彤辉

摘要:为了分析珠江口区域海岸线近年来的发展变化情况,文章基于分形理论,分别对珠江口及深圳段大陆海岸线2005-2019年的变迁趋势采用网格法进行分形分析,得出14年间,珠江口及深圳段海岸线分维数的变化情况。通过对计算结果的分析对比发现,近年间珠江口海岸线整体因开发强度大,人工岸线居多,分维数值变化较小;而深圳段海岸线分维数较整个珠江口有较大幅度增加。深圳段海岸线曲折度提高的原因主要为修复类工程的实施。海岸线分形维数与海岸线曲折程度的正相关系,与海岸带开发利用规划管理要求相符,提出分维数可作为规划用海的重要评估参数。
关键词:海岸线;珠江口;分形理论;分形维数;网格法
中图分类号:P74 文献标志码:A 文章编号:1005-9857(2020)07-0038-04
Analysis of Change of Coastline in the Pearl River Estuary Based on the Fractal Theory
YUE Wen1,YAN Bin2,3,ZHANG Tonghui1
(1.Guangdong Land Surveying and Planning Institute,Guangzhou 511453,China;2.South China Sea Marine Survey and Technology Center,SOA,Guangzhou 510300,China;3.Key Laboratory of Marine Environmental Survey Technology and Application,MNR,Guangzhou 510300,China)
Abstract: Fractal analysis of coastline in the Pearl River Estuary was conducted based on the fractal theory using the survey data from 2005 to 2019.Grid method was used to calculate the changes of the fractal dimension of the coastline.It was found that the fractal dimension value changed little in recent years.It was suggested that marine development resulted in high occupancy of artificial shorelines was the main reason for this result.A significant increase of coastline fractal dimension in Shenzhen section was found,as a result of the restoration program.The positive relationship between the fractal dimension of the coastline and the degree of tortuosity of the coastline is consistent with the requirements of the planning and management of the development and utilization of the coastal zone.The positive relationship between the coastline fractal dimension and the degree of tortuosity of the coastline was consistent with the management requirements for coastal zone protection and utilization.Therefore,the fractal dimension could be used as an important evaluation parameter of the coastal zone development.
Key words:Coastline,Pearl River Estuary,Fractal theory,Fractal dimension,Grid method
0 引言
海岸線是平均大潮高潮时的海陆分界线,具有重要的生态服务功能及开发利用价值,在自然资源管理当中具有重要的战略地位[1]。1967年Mandelbrot的分形理论,提出了海岸线分形与分维概念[2]。叶晓敏等[3]通过对胶州湾海岸线的分形分析,得出较大规模的海岸工程使海岸线分形维数减小,而较小规模的海岸工程和自然过程使海岸线分形维数增大;马小峰等[4]对不同类型的海岸线进行了分形维数分析,进而得知分形维数理论同样适用于多种类型地物组合而成的复合型海岸带。分形维数是描述不规则特征的良好参数,通过遥感技术与分形理论的结合可以研究不同海岸线的变化规律。
珠江口地处粤港澳大湾区中心区域,坐拥1个金融中心、2个特别行政区、2个经济特区、3个自贸区、3个交通枢纽、5个副省级城市。21世纪以来随着经济的高速发展,珠江口海岸带开发利用活动的热度及强度日益增加。本研究以2005年及2019年广东省海岸线数据为依据,提取出珠江口大陆海岸线数据,借助GIS地理信息系统软件平台,计算出该区域海岸线的分形特征,并由此分析其分形维数变化幅值及其原因,进而为科学用海提供理论依据。
1 数据来源及分形分析方法
1.1 分析数据来源
本研究所讨论数据包括2005年珠江口大陆海岸线(数据来源于2004—2006年广东省沿海海洋综合调查与评价)及2019年珠江口大陆海岸线(数据来源于新一轮的海岸线修测)。上述两组数据存在的偏差,主要来源于两组数据的获取精度不同,如测量时使用的卫星遥感底图分辨率和现场实测比例有较大差距,但所选区域几乎没有由围海养殖造成的认定标准不统一,且海岸线提取及认定标准一致。此外,海岸线矢量数据起始于深圳、香港交界,终止于澳门交界,从而避免了数据不连续可能导致的分析误差。因此,所选数据可以作为有效反应珠江口大陆海岸线的变迁分形分析的基础依据。
1.2 分形分析方法
Mandelbrot研究得出海岸线在形貌上是自相似的,也就是局部形态和整体态的相似性,随后创立了分形几何学,初步形成了分形理论[2]。分形形体的整体几何形态分布是处处不规则的,但在不同尺度下,其变化规律又是相同的,局部形态和整体形态呈现自相似性,也就是统计意义上的相似。这种具有自相似性的现象、图形或物理量即为分形[5]。分形理论的提出,在海岸线测绘工作领域的统计意义在于,解释了海岸线的无规则分布形态。其分形维数(海岸线为大于1 小于2的分数值)则解释了无法用整数维数表征的物理量的分布特征[6]。常用的海岸线分形维数计算方法有两种[7],本研究采取网格法计算珠江口海岸线的分形维数。
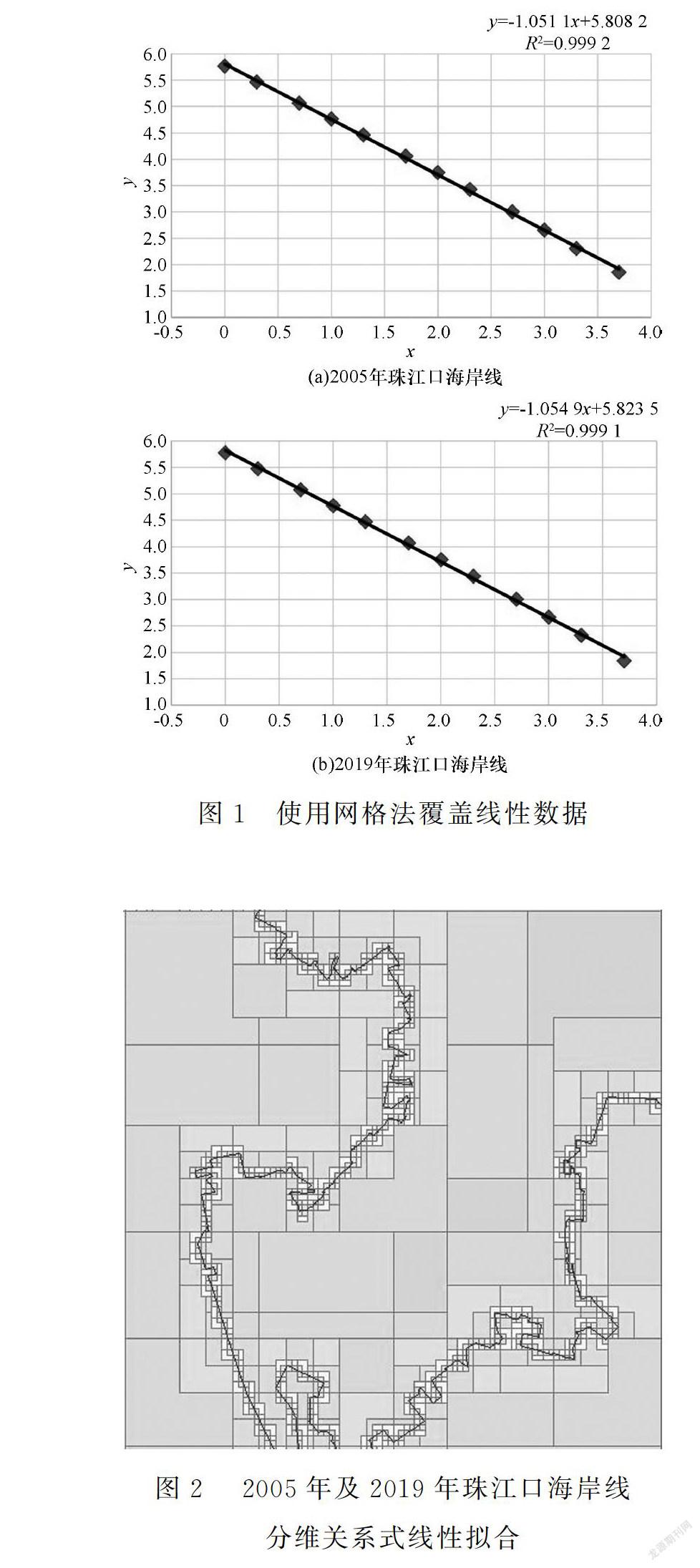
网格法是使用不同边长的正方形网格覆盖海岸线,统计不重叠覆盖的线状网格信息,得到不同的网格数目,最终计算出其分形维数。通过GIS软件采用网格法对珠江口海岸线(图1)进行覆盖,其中正方形边长为ε,覆盖海岸线且不重叠覆盖的网格数目为N(ε)。根据分形理论,即lgN(ε)=-Dlgε+A式中:A为待定常数;D为覆盖线状数据的分形维数。
2 分维数计算
使用GIS软件,对目标珠江口海岸线进行网格覆盖,网格正方形边长分别取值1 m、2 m、5 m、10 m、20 m、50 m、100 m、200 m、500 m、1 000 m、2 000 m、5 000 m,通过网格法分析计算,得出不同的网格数目。根据两组数据的对数关系,将得到的数值进行线性拟合得出(图2),2005年珠江口海岸线线形方程为y=-1.051 1x+5.808 2,D值为1.051 1;2019年珠江口海岸线线形方程为y=-1.054 9x+5.823 5,D值为1.054 9。
3 珠江口岸线变迁的分形维数规律
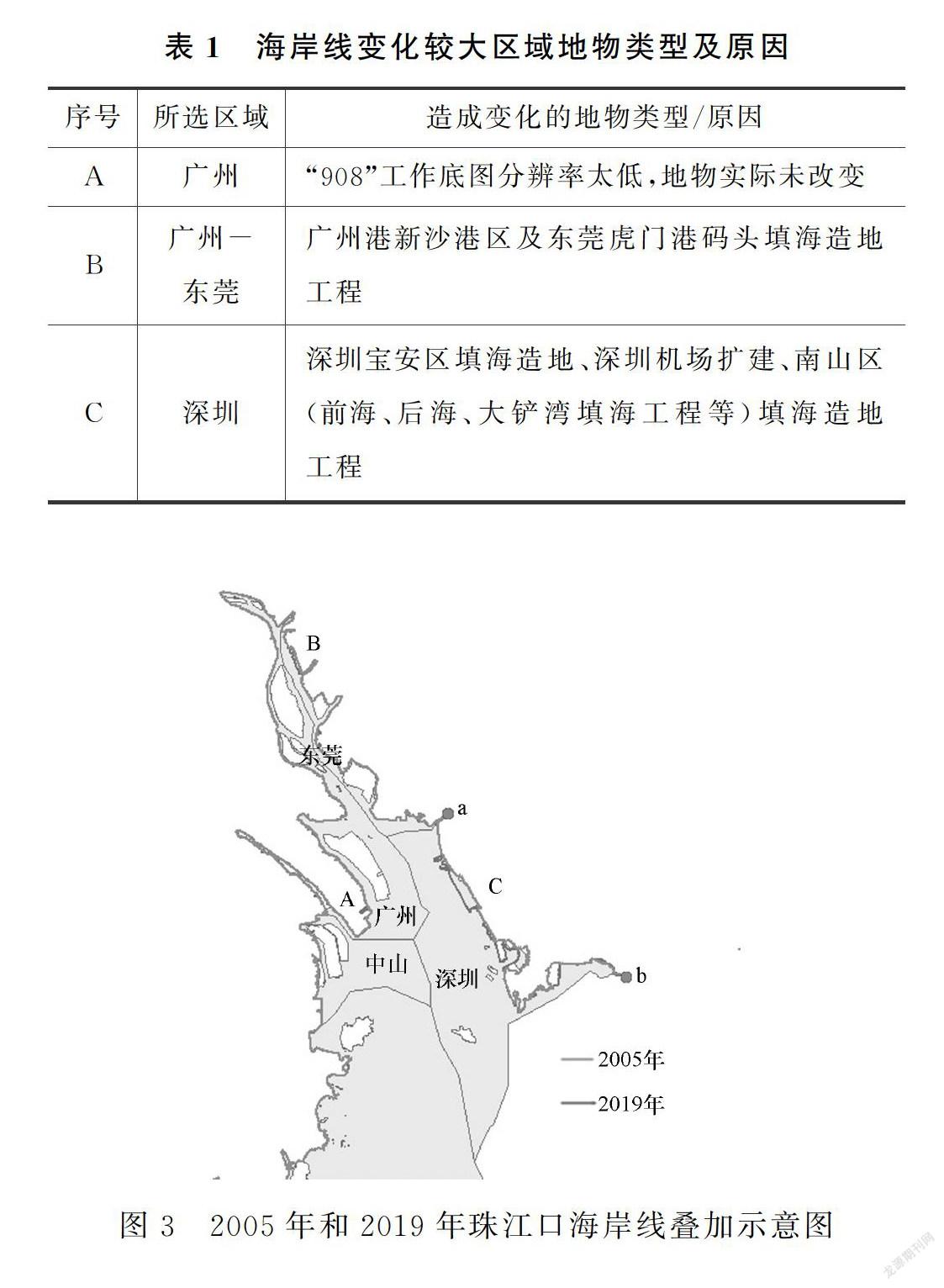
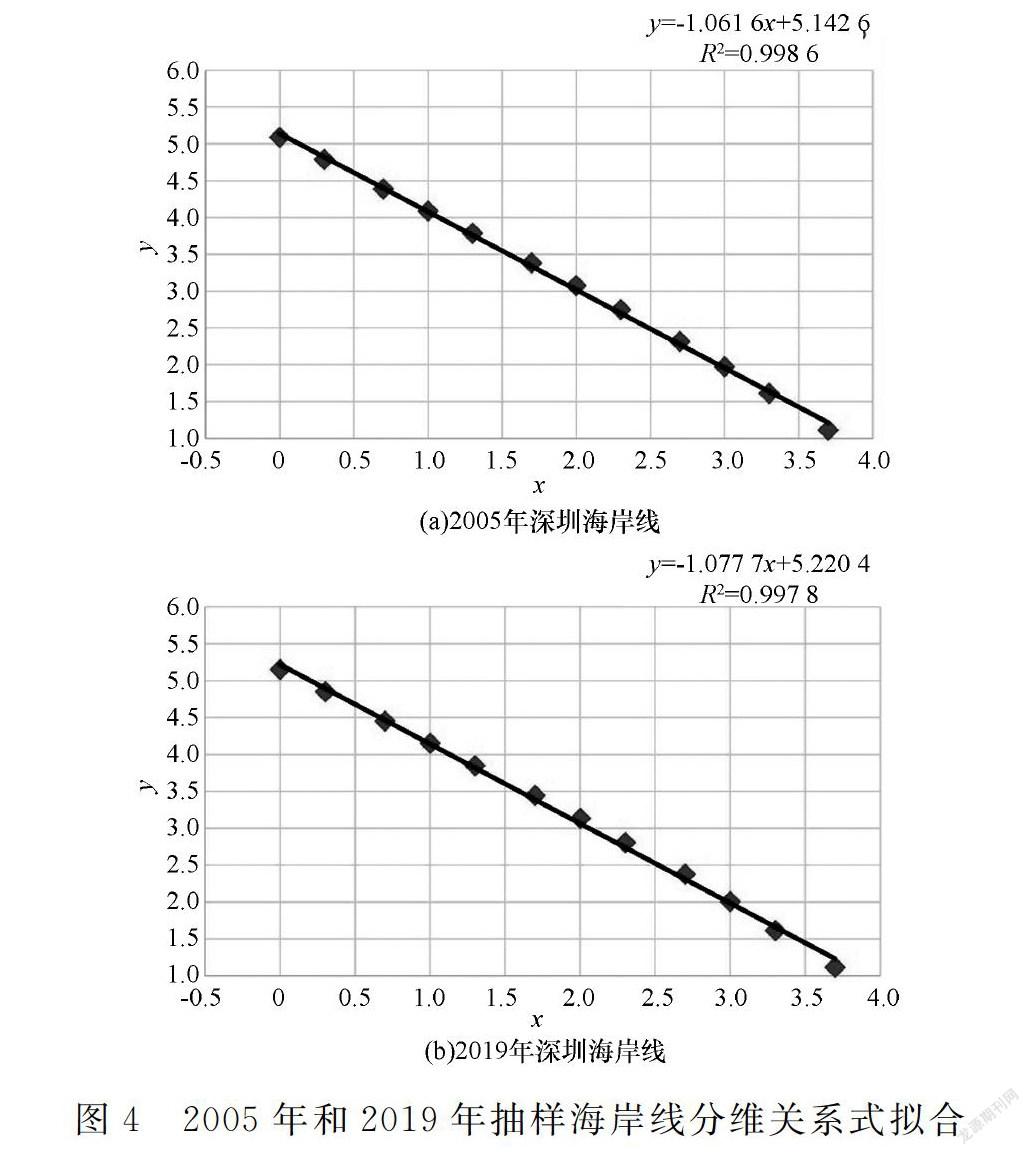
根据Mandelbrot研究结论,海岸线分维值的大小范围为 1 14年间,珠江口变化较大区域集中在深圳西海岸(表1及图3),使用GIS软件采用网格法对抽样区域,即深圳市宝安至南山区后海海岸线进行覆盖,使用测得数据得到ab段线形方程关系式(图4)。 深圳市ab段海岸线分形维数增大了0.016 1,是珠江口分形维数变化值的4倍多。ab段海岸线分形维数增幅较大,表示2019年较2005年海岸线凹凸曲折部分占比增大。ab段海岸线分形维数增大是珠江口海岸线分形维数增大的主要原因。 深圳市ab段海岸线2005—2019年变化主要分3個阶段,排除冲淤因素,填海工程是主要成因。第一阶段为大规模填海造地期,第二阶段为重点工程配套建设期,第三阶段为生态修复期。2001年由于南山区后海、前海、大铲湾填海工程开始施工,2005—2012年,南山区前海、后海、大铲湾填海工程基本完成,期间前海、后海区域海岸线折弯取直,该区域海岸线长度大幅减少。第二阶段2013—2017年,除深圳机场扩建工程以外,均为小规模造地工程,地铁11号线、LNG、码头港口等城市配套工程落地。第三阶段,南山区通过城市交通滨海休闲景观改造工程打造深圳湾公园海岸线,2008年至今逐步修复成蜿蜒曲折并具有红树林生态功能和自然海岸形态的修复岸线。 5 结论 (1)珠江口海岸线分形维数2005年为1.051 1,2019年为1.054 9,抽样ab段海岸线2005年分形维数为1.061 6,2019年分形维数为1.077 7,与分形理论研究结论相符。获取的海岸线分形维数回归方程相关系数计算值R2均在0.99以上,因此网格法计算所得分形维数可作为目标海岸线表征的良好参数。 (2)珠江口海岸线变化区域主要在广州、东莞、深圳三地,其中深圳市海岸线变化较大,与其海岸线分维数变化规律相符。 (3)珠江口海岸线人工岸线类型达到90%,人工岸线防洪属性决定了珠江口海岸线受水动力冲淤环境影响较小。2005—2019年珠江口海岸线变迁的主要因素为填海造地工程,通过抽样ab段海岸线分维数分析,深圳市填海工程是珠江口海岸线分维数增大的主要因素。 (4)2005—2019年深圳地区建设的海岸带修复工程总体上增加了海岸线长度,而其分维数的增加意味着海岸线曲折度也同时有所提高,即,分维数的增加与海岸带整治修复工程密切相关。在合理规划和修复海岸线的前提下,适度开发利用可提升海岸带服务价值,同时也与海岸带综合利用管理中的占补平衡管理理念相符。因此,分析理论可服务于海岸带综合管理开发利用总量控制,分维数是衡量海岸线变迁的良好参数,可作为规划用海的重要评估参数。 参考文献 [1] 熊兰兰.加快推进广东省海岸线整治修复的建议[J].智库时代,2018(20):80-82,105. [2] MANDELBROT B B.How long is the coast of Britain· Statistical selfsimilarity and fractional dimension[J].Science,1967,156(3775):636-638. [3] 叶小敏,纪育强,郑全安,等.胶州湾海岸线历史变迁的分形分析[J].海洋科学进展,2009,27(4):495-501. [4] 马小峰,邹亚荣,刘善伟.基于分形维数理论的海岸线遥感分类与变迁研究[J].海洋开发与管理,2015,32(1):30-33. [5] 张国祺,李后强.分形理论对世界认识的意义[J].大自然探索,1994,13(47):11-16. [6] 何隆华,赵宏.水系的分形维数及其含义[J].地理科学,1996,16(2):124-128. [7] 朱晓华.海岸线分维数计算方法及其比较研究[J].黄渤海海洋,2002,20(2):31-36. 基金项目:自然资源部南海局海洋科学技术局长基金重点项目(180107). 作者简介:岳文,工程师,研究方向为海洋生态、海域海岛开发利用 通信作者:颜彬,工程师,博士研究生,研究方向为海洋地质学及地理信息系统

