古印度的算术

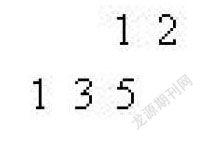
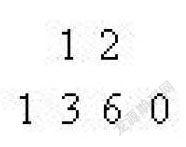
印度是世界上文化发达最早的地区之一.古印度的数学家多以天文学为职业，取得的数学成果多半是根据经验总结，很少给出具体的推导和证明，因此，古印度在算术、代数和三角知识方面取得了较大的成就.

十进位值制记数法和印度-阿拉伯数码的出现，不仅在数学史上，在全人类文化史上都具有十分重要的意义.这种记数法的产生和完善经历了相当长的时期.

在十进位制记数系统建立以前，在印度出现过各种不同的数字和记数法，现在很难研究出它们之间的承袭关系.从公元前4世纪到公元3世纪，在现今的东阿富汗地区和旁遮普北部风行的所谓音节数字（图1）与当时的古印度音节文字有关.这可能是一种十进非位值制系统.数字1，4，10，20和100用特殊记号表示，其它数由加法原则写出，数字从右往左书写.

很久以来，在印度广大领土上传播着婆罗门数字，这是十进位记数法发展的较高阶段，这种数字形式保持了一千多年（图2），佛教和婆罗门数字一起被传入其它国家，在个别地区，这种数字一直沿用到19世纪.

一般说来，在印度的各种数字系统中，至少从公元前2世纪起，数字1，2，…，9就存在单独的符号，这些特殊符号的存在是产生十进位值制记数法的基础.单位1出现在表示单数事物，如“太阳”“月亮”的词语中;而数字2出现在“双生子”“眼睛”“手”这类词语中;数字5出现在“感官”（即五官）“手掌”這类词语中;等等.数字的书写顺序是从低位向高位，古印度历数书中的天文表就用这样的顺序表示数字，缺位时用特殊符号标出.

阿耶波多Ⅰ（Āryabhaṭa，公元476年-550年）的著作中用音节表示数字，完全没有位值制的特点.每一个数k·10n（k=1，2，…，9;n=0，1，2，…）都被特殊音节所代替，丰富的梵文字母能够给充分大的数字命名.但是，他的学生——婆什迦罗（Bhāskara，公元540年-629年）却改进了这种记数法，使数字的音节具有位值性，他还引进了表示空位的音节.

大约在6世纪上半叶，印度人改变了数字中数位的书写顺序，开始从高位向低位书写，这可能是受希腊人的影响.位值制记数原则包含这样三个因素：1.每一位数都由该数位单位乘以相应的数字;2.省略每个数位单位的符号;3.用确定的符号（零号）表示任何数位上的空缺.所有这些因素在印度首先是局部地、口头地应用，然后过渡到广泛地、文字上地普及.不晚于6世纪，在印度产生了新的、整数的十进位值制记数法，即用9个数字和表示零的小圆圈可以写出任何数字，每个位置上的数字有明确意义，同一个数字在不同位置上则代表不同数值.

7世纪中叶，印度的记数法开始向西方传播.8世纪末，这种记数法传入巴格达哈利发的宫廷中，经阿拉伯人的改进传入欧洲后就被称为印度—阿拉伯数字了.

印度的算术文献中记载了整数和分数的八种运算：加法、减法、乘法、除法、平方、开平方、立方和开立方.某些运算是有明确定义的.

例如，阿耶波多Ⅱ（AryabhataⅡ）定义加法是把一些数合并为一个数，而减法则是从一个数中拿掉其中一部分.婆什迦罗Ⅱ认为乘法和除法可以相应地转化为加法和减法.

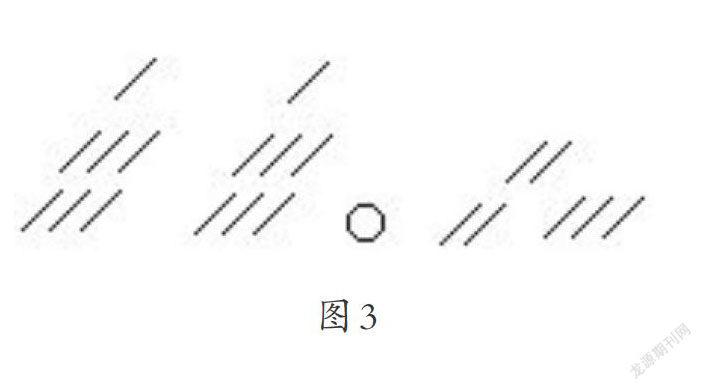
古印度广泛使用计算板.梵文中“算术”一词就是由“计算”和“板”两个词复合而成的.但是在更早的时期，稍复杂的运算是在用贝壳作成的古算盘上进行的.计算人员手拿一个装有几百个长形贝壳的口袋，在算盘各栏中摆出数字1，2，…，9;还有12个圆形贝壳，用来表示零.例如数字52077被摆成图3的形状.斜线表示长形贝壳，圆圈表示零.现在正统的佛教徒——婆罗门学者还使用这种方法进行计算.

使用算盘计算需要熟记一些法则，即加法的进位和减法的借位.乘、除法则在加、减法的基础上进行.

记载算式的文献很晚才出现.在古代，凡是书写出来的数字不是为了进行计算，而是为记录经文中出现的年代.后来出现了文字运算，但只给出结果而没有中间运算步骤.这是因为当时的计算工具是一个铺满沙土的盘和一根削尖的木棍.字要写得比较大才能认清，这样一个数在完成它的作用后就被擦掉，以保留书写的空地.

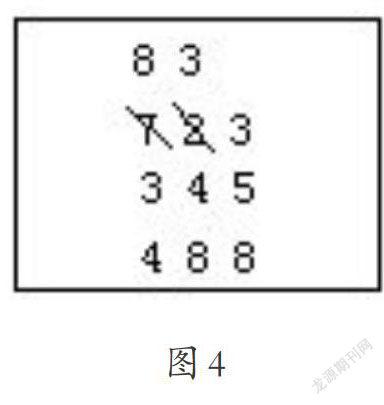
加法是从最高数位开始进行计算.例如345+488是这样进行的：把一个数写在另一个数的下面，对齐数位，并在书写板的上端留出一些空地.3+4=7，把7写在最左一列的上头;然后4+8=12，把7改为8，后面写上2，因此7被擦去，而改为82;最后5+8=13，把82中的2改为3，后面再写个3，就得到结果833”（图4）.

做乘法有几种不同的方式.比如，在沙土板上写出

首先将5×12，把5擦掉，写上60， 再把乘数12向左移动一位，得到

然后将3×12，得36，把6加在1360的6上，擦去其中的6，写上2，往3上加1，把1360中的3改为4，再移动乘数12，得到

最后将1×12，把2加在4上，擦掉4，写上6，1字保留不动，得乘积为1620.

另一种计算乘积的方法，与我们现在的程序语言很接近.在计算板上画出彼此垂直的方格，再把每个格子都用同个一方向的对角线分开，沿着格子的两个边写上乘数，将中间的乘积写在右下方三角形中，在需要进位时将所得的结果记在左上方三角形中，然后依对角线进行加法运算.还是以135×12为例，这种方法的程序为

有时为了化简运算，古印度人会采取一些简单变换，如135×12=135×（12+8）-135×8或135×12=135×（12-2）+135×2.

印度人的算术运算方法，后来被阿拉伯人和欧洲人所采用.

带有数字0的运算是位值制系统计算的重要内容.印度人不仅仅把0看作是“一无所有”或空位，而且把0看成是一个数.这是对印度算术作出的一大贡献.这种做法在3世纪时已经出现.在天文学家瓦拉哈米希拉的《五大历数全书汇编》（约505年）中记载了对零实行的加、减运算.

一个多世纪以后，婆罗摩笈多在他的著作中给出了比较完整的叙述：“负数减去零是负数，正数减去零是正数，零减去零还是零;零乘正数、负数或零都是零……零除以零空无一物，正数或负数除以零是一个以零为分母的数.”婆什迦罗Ⅱ把a÷0称为Khahara，与无穷大的含义相似.

在印度算术中，分数也有较完整的理论.分数的写法与中国古代算筹分数记法一样，分子在上，分母在下，没有分数线.若是带分数，则需将整数部分写在分子之上.例如

在进行整数与分数运算时，把整数写成分母是1的分数.分数四则运算用下列法则：

在某些情况下，需要把一个分数化为几个单位分数之和，然后进行计算.

在印度，关于开平方和开立方的最早记录出现在阿耶波多Ⅰ的著作中.他把运算法则用诗歌的形式写出来，这是很难理解的.9世纪数学家施里德哈拉所敘述的法则较为详细.我们以54756的开平方为例说明他的方法.

写出数字54756，在其奇数位的上方画出竖线，在偶数位的上方画出横线，得到

找出不超过5的最大平方数，即4，把它写在下一行，并从5中减去4 ，得到

用14除以4，商3余2，擦去14，写上2，得到

从27中减去3的平方，即9，余18，擦去27，写上18.把3加倍后写在4的后面，得到

重复上面步骤.185除以46，商4余1，擦去185写上1，得到

从16中减去4的平方，得零，擦去16，把4加倍写在46后面，最后把468除以2得234.这就是54756的平方根.

这种程序与中国《九章算术》中开平方的计算步骤有所不同.对于分数a/b，如果分母b不是完全平方数，那么需要将其变换为ab/b，再进行计算.为了提高精确度，古印度数学家在分子上乘上10的偶数次幂.

由于在计算板上运算不能保留中间运算的步骤，所以印度学者采用一种被称为弃9法的验算方法，它的依据是这样的一个事实：任何整数和它的各位数字之和除以9的余数相同.阿拉伯算术中也采用弃9法验算，这来源于印度，后来又传入欧洲.

在印度的算术著作中，有大量丰富多彩的以诗歌形式表述的算术问题.这些问题涉及了假位法（单设法和双设法）、三位法、百分率和级数等.其中还有大量来源于实践的问题，也有一些是纯粹作为消遣和娱乐的题目.

在这些问题中单设法占相当的比例.印度数学家马哈维拉（Mahāvīra） 用单设法解决了大量的代数和几何问题.婆什迦罗Ⅱ也研究过这种方法，他的《丽罗娃提》中有这样一个问题：“从一束清洁的莲花取出其三分之一、五分之一和六分之一，分别献给湿婆、毗瑟拏和苏利耶，再给布赫瓦尼四分之一，只剩下6只莲花，送给尊敬的教师，请说出莲花的数目.”婆什迦罗Ⅱ设所求数为60，即3，4，5，6的最小公倍数，由此可术得出应剩3只莲花，则所求的的解为60*6/3=120.

在被发掘的古印度数学手稿《巴赫沙里手稿》中，单设法不仅用于解形如ax=c的方程，还应用于解形如ax+b=c的方程.如设x1为所求数，由此得出

三位法在印度算术中占核心地位，它能够简便地解决各种实际问题.三位法就是求下列具有三个已知数a，b，c的比例式中的x.婆罗摩笈多认为：“在三位法中，第一项与第三项必须是同类的（单位相同的数量），第二项、第三项相乘，以第一项除得结果.”

婆罗摩笈多还提出了“反三位法”.即求比例中的x.例如中世纪著名的工程问题：“a个人完成一项工作要用b天，问同一项工作c个人做要用多少天？”后来还出现了“五位法”“七位法”“九位法”和“十一位法”.

以“五位法”为例，五位法就是求满足比例式中的x，易求出x=abd/ce.显然，五位法解决了两个三位法的问题.同理，七位法中就有三个三位法，如此类推.

三位法从印度传到西方，在几个世纪之内都是解决算术问题的主要方法，直到19世纪，欧洲学校的教材才逐渐取消了三位法.

纵观古印度的数学发展，不难发现印度的算术简单实用，数学家也并不多.和中国的数学发展历程有很多相似之处.