基于滑动熵互相关系数与k-means聚类算法的局部特征尺度分解分量筛选方法
盛沛

摘要:提出了一种利用滑动熵以及互相关系数算法对局部特征尺度分解所得分量进行筛选分类的方法。首先对原始信号进行局部特征尺度分解,其次对分解所得的任一分量以及原始信号通过移动起始点的方式计算熵值并计算每一个熵值序列与原始信号的互相关系数,最后利用k-means聚类算法对上述互相关系数进行分类,即可实现分量的筛选。仿真结果表明,该方法能够有效对局部特征尺度分解所得分量进行筛选,较同类方法具有较大的类间距离。
Abstract: A method of filtering and classifying components obtained from local feature scale decomposition is proposed by using sliding entropy and correlation number algorithm.First local characteristics of original signal scale decomposition, on the second income of any component and the original signal is calculated by means of mobile starting point each entropy is calculated entropy and sequence number of a mutual relationship with the original signal, the use of k - means clustering algorithm to classify the amount of the relationship between each other, the component can be realized in screening.The simulation results show that this method can effectively screen the components obtained from local characteristic scale decomposition and has a larger inter-class distance than similar methods.
关键词:局部特征尺度分解;分量筛选;熵值法
Key words: LCD;component selection;entropy method
中图分类号:TN911;E917 文献标识码:A 文章编号:1006-4311(2020)25-0237-04
0 引言
诸如经验模式分解(Empirical Mode Decomposition,EMD)[1]、局部均值分解(Local Mean Decomposition,LMD)[2]、局部特征尺度分解(Local Characteristic-scale Decomposition,LCD)[3]-[4]等分解方法的优点是具有自适应性,可以在时间尺度上自动将信号按照不同频带进行分解。但是,也正是由于其自适应性,导致其分解的结果相对“粗糙”。当信号在几个特定频带能量聚集性较好时,这些算法可将故障特征分离在少数几个分量中。但实际上这种情况多见于仿真实验的简单几个信号叠加的情况,如文献[5]等。在大多数情况下,实测的信号故障信息往往在多个内禀尺度分量(Intrinsic scale component,ISC)分量中均有体现,这将对后续处理造成很大不利。在第二种情况下,少数几个ISC分量不能有效檢测出故障特征或检验效果不理想,而取多个ISC分量将会使计算量增大。更进一步讲,第几个ISC分量存在故障信息是未知的,选取过少则信息丢失,选取过多则信息冗余、计算量加大。文献[6]选取前几个分量进行故障特征提取及算法比较是基于处理的信号频段考虑,缺乏理论依据、略显武断。
1 算法原理及相关概念
在分量筛选方面,相关学者做出了大量研究,目前主要方法一是基于互相关系数,二是基于分量自身信息含量的。前者的理论依据是有用分量必然与原始分量相关性较高,这是从降噪角度出发的一种思考方式,即将分量筛选的过程当成了一种降噪的过程。而后者的理论依据是,诸如峭度、信息熵指标等都是信号非高斯性的一种常用度量指标,大多数情况下信号的高斯特性是数据无序性的一种体现,在工程应用中往往是最“无趣的”,因此,对于故障诊断而言其必然是无用的应该舍去的。文献[7]将二者结合起来,将分解所得的各分量与原始信号互相关系数较大者以及峭度较大者作为有用分量。这三种方法都具有足够清晰的物理意义,但从实际应用情况看来,仍存在指标数值区分度不够大、筛分结果与实际不符等问题。为使有用分量筛选的结果更加准确,本文定义了一种表征信号蕴含故障信息程度的量值——滑动熵-时间序列,将各分量与原始信号滑动熵序列的互相关性作为有用分量筛选指标的方法,具体原理如下:
1.1 互相关系数
互相关系数可以表征两个信号幅值之间的相互依赖关系,设两个信号为x(t)、y(t),其互相关系数可表示为:
有用分量与原信号的互相关性系数略小于该分量的自相关系数(分量自相关系数约等于1);而非有用分量与原信号的互相关系数很小。可通过互相关系数来判定该分量是否为有用分量[8]。
1.2 熵的定义
由信息论可知:在所有随机变量中,高斯变量熵值最大。进一步讲,如果信号是高斯的,则其是最没有结构特征的。在信号处理领域,那些具有长而尖的概率密度的信号,其熵值应当最小。这往往也是人们最“喜欢”见到的信号,因为它非常有助于进行聚类。熵是信息论中的基本概念之一,离散随机变量X的熵可以定义为:
1.3 滑动熵的定义
熵值反映的是信号的无序特性,但对细节反映不足,为了从时序细节上观察信号中无序特征,本文提出一种通过滑动起始点计算各信号段熵值的方法,得到熵值序列。具体计算过程为:
步骤1:对信号x(n)(n=1,2,…,N),确定合适的计算长度l。l的选择以体现信号中蕴涵的周期成分为原则,通常取l=5~25。
步骤2:分别以x(i)(i=1,2,…,N-l+1)为起点,依次向后截取l个数据点,计算熵值K(i),将K(i)依次排列:
得到滑动熵值-时间序列。
1.4 滑动熵值-时间序列互相关系数
滑动熵值-时间序列即可描述信号非规律特性又具有一定的细节可辨特性。相较于直接互相关系法与熵值法更加贴合分量筛选的目的,即找到对故障状态分类贡献最大的ISC分量。
1.5 基于滑动熵互相关系数与k-means聚类算法的分量筛选
经过上述计算过程,对故障诊断有用的和无用的分量已经更容易区分,但仍需要一种方便操作的分量筛选方法。为了避免人为因素干扰,最直接的办法就是利用聚类算法进行二分类。聚类具体步骤为:
其中:Je为误差平方和聚类准则,对不同的聚类方案,Je的值不相同,使Je最小的聚类即是最优结果。
综上所述,本文的分量筛选流程可按以下步骤进行:
步骤1:对故障信号进行LCD,得到若干个ISC分量。
步骤2:计算每个ISC分量与原始信号的滑动熵值-时间序列的互相关系数。
步骤3:以该互相关系数作为聚类指标,采用k-means聚类算法将所有ISC分量进行两分类——有用分量和无用分量,前者整体互相关系数较大,而后者较小。
2 分量筛选方法实例验证
[算例 1] 考察如下信号:
式中:表示信噪比为SNR的高斯白噪声,SNR按每个采样点计算,单位dB;f1、f2分别为可变频率。选取一组信号,不添加噪声,原始信号如图 1(a)所示,进行LCD后仅得到图 1(b)、(c)两个ISC分量和一个图 1(d)的剩余信号。可以看出,在信噪比很高的情况下,算例中的合成信号被很好地分解为两个分量。那么在此种情况下,利用文献[6]方法将导致后续智能学习机的算法出错。本文在尝试利用文献[6]方法进行后续实验时,尝试将缺失分量置零并补齐,但效果仍不甚理想。
在另一方面,对于实测信号而言,大部分实测信号的分解情况则刚好相反——的确会出现文献[6]所述的超过五个分量的情况。但其有用特征分量的确定却需做进一步讨论。
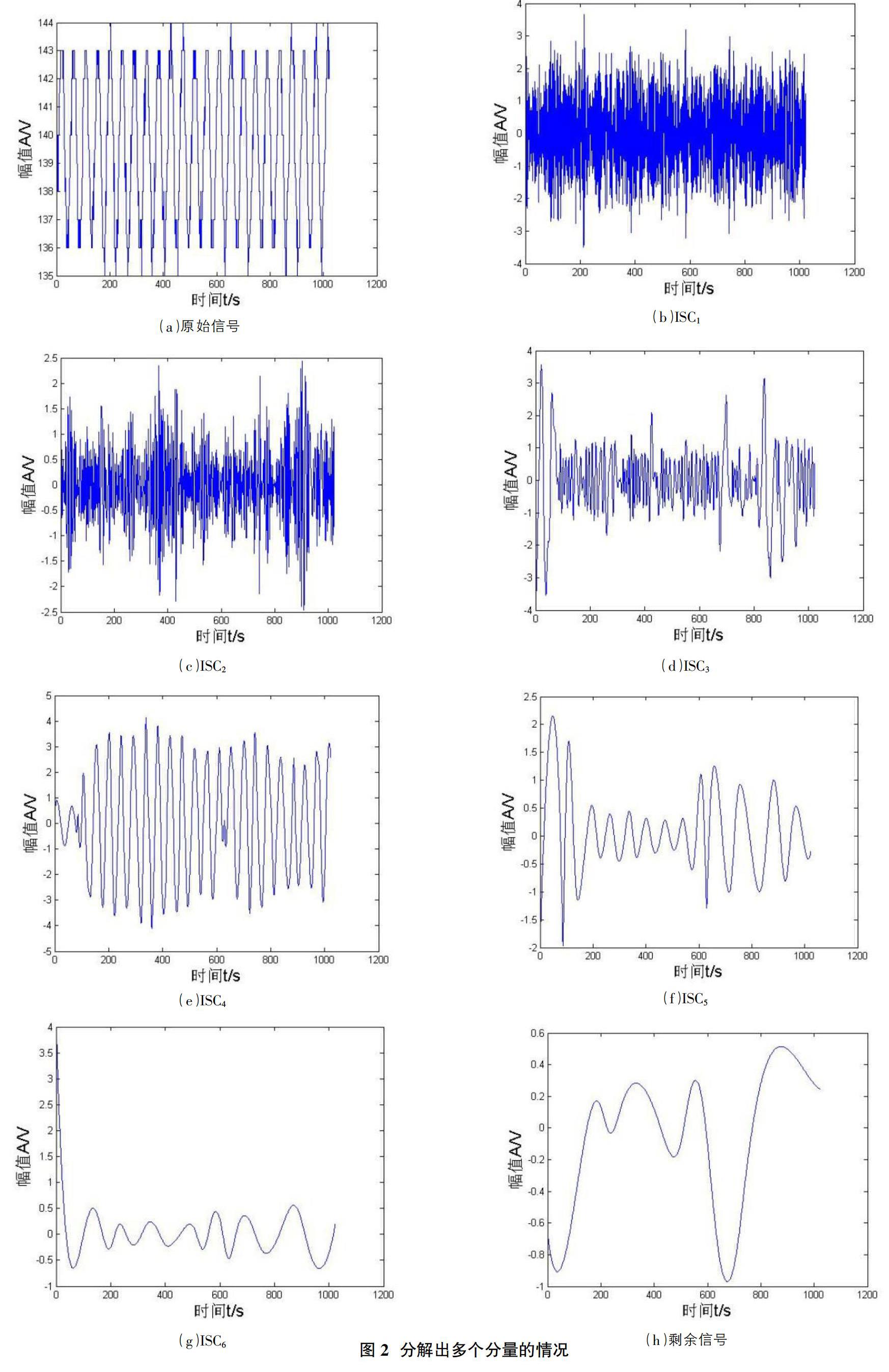
[算例 2]仍在上例中选取一组信号,但此次添加一微弱高斯白噪声(SNR=5),对其进行LCD并观察此次分解结果。混有噪声的原始信号如图 2(a)所示,其分解产生的分量及剩余信号如图 2(b)~图 2(h)所示。显然的,第一分量为噪声分量,文献[6]取固定前5个分量的做法是错误的。
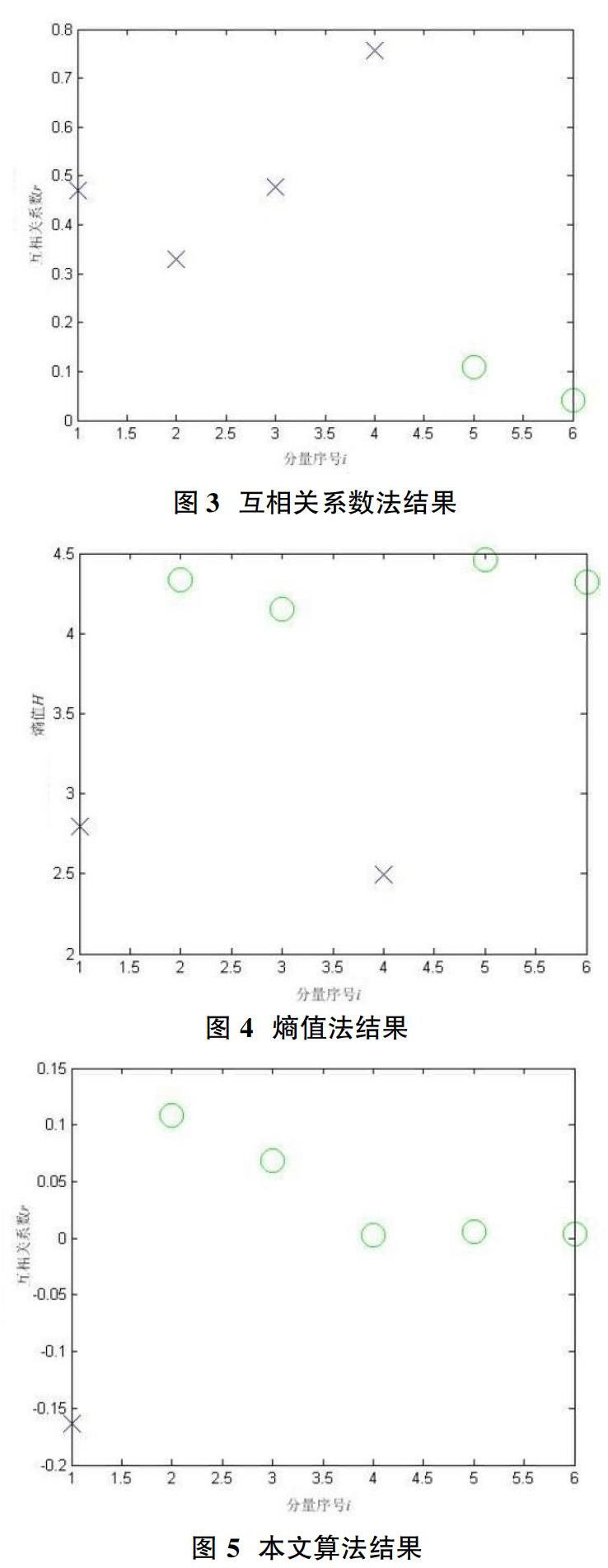
[算例 3] 为了验证上述分量筛选方法有效性,对上例中得到的各ISC分量分别计算两种分量筛选指标:各分量与原始信号直接求取所得到的互相关系数、各分量的滑动熵-时间序列互相关系数,并将结果列于表1。
从以上结果可以看出:①互相关系数法排序结果为:ISC4、ISC3、ISC1、ISC2、ISC5、ISC6。按照聚类算法自动聚类,其效果如图3所示。ISC5、ISC6可视为噪声或虚假分量,分量筛选结果与前面的分析是一致的,但有用分量与非有用分量间的数值相差不大,不利于区分。②按分量熵值将各分量排序,结果为:ISC5、ISC2、ISC6、ISC3、ISC1、ISC4。按照聚类算法自动聚类,其效果如图4所示。ISC5、ISC2、ISC6、ISC3的熵值较大,是无用分量,结论与事实不符。因此,依据熵值选取有用分量是存在问题的。③本文算法排序结果为:ISC2、ISC3、ISC5、ISC6、ISC4、ISC1。按照聚类算法自动聚类,其效果如图5所示。后五个ISC视为有用分量;ISC1视为非有用分量。这与噪声分量多几种在高频部分的论述是十分吻合的。因此依据滑动熵-时间序列互相关系数选取有用分量是准确的。进一步对滑动熵-时间序列互相关系数与直接互相关系数算法在数值方面进行比较分析可知:在有用分量与非有用分量之间,本文算法类间距离相对值更大,区分更加明显。
3 结束语
本文算法是在结合了熵值法及互相关系数算法在局部特征尺度分解有用分量筛选应用方向的成果基础上产生的,仿真实例证实了其有效性。虽然本文算法数值整体偏小,直观上看,本文算法相关性数值较小,但是本文追踪的是信号的非规律性,更能体现故障的本质。本文认为,在故障诊断领域,相对大小相较于绝对大小更有利于達到自动分类的效果。
参考文献:
[1]Huang N E, Shen Z, Long S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings of the Royal Society of London. Series A: Mathematical, Physical and Engineering Sciences, 1998, 454(1971): 903-995.
[2]Smith J S. The local mean decomposition and its application to EEG perception data[J]. Journal of the Royal Society Interface, 2005, 2(5): 443-454.
[3]程军圣,郑近德,杨宇.一种新的非平稳信号分析方法——局部特征尺度分解法[J].振动工程学报,2012,25(2):215-220.
[4]程军圣,张亢,杨宇,于德介.局部均值分解与经验模式分解的对比研究[J].振动与冲击,2009,28(05):13-16,201.
[5]郑近德,程军圣,聂永红,罗颂荣.完备总体平均局部特征尺度分解及其在转子故障诊断中的应用[J].振动工程学报,2014,27(04):637-646.
[6]张清华,王磊,孙国玺,雷高伟,邵龙秋.基于经验模态分解的无量纲指标故障诊断定位[J].上海应用技术学院学报(自然科学版),2016,16(01):17-21.
[7]崔伟成,许爱强,李伟,孟凡磊.基于滑动峭度相关性准则的局部特征尺度分解分量筛选方法[J].计算机测量与控制,2016,24(10):233-235,239.
[8]张学工.模式识别[M].北京:清华大学出版社,2016.

