考虑非线性流变的一维修正UH模型

刘忠玉，张家超，夏洋洋，崔鹏陆

(郑州大学 土木工程学院,郑州 450001)

在软黏土地区，因工后沉降问题而导致的工程事故频频发生，给国家造成了巨大的损失. 为此，大量学者[1-4]投入到软黏土变形机理的研究中，并发现经典太沙基理论并不总能较好地模拟软黏土变形过程的所有现象. 有关固结试验和现场观测[5-6]表明，软黏土的流变特性是影响软黏土变形过程的重要因素之一. 因此，不少学者通过试验探讨了影响流变过程的因素，如荷载强度[7]、超固结比[8]等. 在理论研究方面，一些学者[9-10]已考虑流变特性，建立了两类形式的黏弹性或弹黏塑性本构关系：一种是基于元件理论而提出的，另一种是基于弹黏塑理论而提出的.对此，袁静等[11]曾进行过比较，认为基于弹黏塑性理论而提出的本构关系更有利于描述软黏土的变形特性. 这类本构模型最早的工作是由Bjerrum[12]进行的，他认为土的变形过程可划分为可恢复的瞬时压缩以及不可恢复的延时压缩两部分，并提出了一维等时间线模型. 而Yin等[13-14]认为土体的黏性变形与塑性变形应该统一起来，并提出了“等效时间”的概念，建立了一个与时间相关的弹黏塑性(EVP)本构模型. 后来，姚仰平等[15]在Bjerrum瞬时压缩线的基础上，提出了相对瞬时压缩线的概念，结合超固结统一硬化(UH)本构模型，提出了可以考虑时间效应的UH模型. 除考虑时间效应[15]外，学者们在UH模型建模思想[16-18]的基础上，也开发了可以考虑其他因素的模型，如温度效应[19]、各向异性[20]、土的结构性[21]、胶结作用[22]以及负蠕变效应[23]等. 这些也说明UH模型具有较高的应用价值.

在上述考虑土体黏滞性的本构模型中，有些已被应用于饱和黏土的一维固结分析中，并成功模拟了加载初期由黏土黏滞性引起的孔压增高现象[24-25]. 然而，上述本构模型均假定流变过程为线性的，常采用Buisman公式来表示流变引起的孔隙比减小值Δe与时间t的关系，即

Δe=Cαlg(t/t1).

(1)

式中:t1为主固结完成时间;Cα为次固结系数.但式(1)无法反映t=0的情况，所以，有学者将其改为[15,26]

Δe=βlg[(t+t0)/t0].

(2)

式中:t0表示参考时间或单位时间；系数β与Cα基本相同，并可用后者代替.

值得注意的是，当时间t趋向于无穷大时，式(1)或(2)表示的孔隙比减小值都趋向于无穷大，也就意味着土中的孔隙可以无限被压缩，这与事实是不相符的. 不少试验和理论分析[27-33]证明，次固结系数并不是常数，而是一个与时间相关的量. 其中，Yin[29]建议引用双曲线方程[30]来表示由流变引起的变形[31-32]，而胡亚元[33]则进一步将次固结系数表示为时间和超固结比的函数.

为进一步探究黏性土流变固结机理，参考Yin[29]的思想，考虑了次固结系数的时间效应，修正了统一硬化UH本构模型，并通过一维固结试验验证了修正UH模型的有效性. 随后也应用文献资料对上述修正UH模型进行了验证，从而进一步确定了该修正模型的适用性.

1 UH模型修正及非线性流变参数求解

1.1 UH模型的修正

统一硬化UH本构模型[15]是在修正剑桥模型的基础上进一步发展起来的，其一维应变增量及塑性应变增量可分别表示为

(3)

(4)

(5)

(6)

(7)

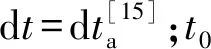
M=6sinφ/(3-sinφ),

(8)

(9)

χ=M2/[12(3-M)],

(10)

(11)

(ta+t0)/t0=R-α.

(12)

式中α=(CC-CS)/Cα.

式(7)所示的延时应变增量，实际是由土的流变引起的，其与式(2)是等效的. 因此，如果Cα与时间无关，也会遇到前述式(2)所遇到的土体被无限压缩的问题. 为避免该问题，考虑次固结系数的时间效应，即参考Yin[29]的方法，认为次固结系数与时间相关，并表示为

(13)

式中:Cα0为初始次固结系数,A为非线性流变参数.可以看出，当t趋于无穷大时，次固结系数趋于零. 将式(13)替代式(2)中的β，即

(14)

令t→，则Δe→A，即A就是由流变引起的孔隙比减小值的极限，为可通过试验确定的有限值.这样就不会出现因流变因素而导致的土体被无限压缩的问题.

将式(14)等号两边同时微分可得到类似式(7)的增量形式，即

(15)

通常，Cα0为远小于1的数，则其平方会远小于其本身，即L会远小于N. 因此，延时应变增量可仅用式(15)中的第二项近似表示，即

(16)

同时，式(12)中的参数α应调整为(CC-CS)/{Cα0/[1+(Cα0/A)lg(t+t0)]}.

1.2 非线性流变参数求解

尽管老化时间ta与加载时间t并不相等，但dt=dta[15]. 因此，对于超固结土，设再加载开始时(t=0)的初始老化时间为ta0，则老化时间ta=t+ta0. 很明显，当加载时间很长时，ta+t0的对数与t+t0的对数近似相等.此时，式(14)可变为

(17)

式(17)表明，当t很大时，lg(t+t0)/Δe与lg(t+t0)为线性关系. 所以，将固结完成后(即主次分界点以后)孔隙比e随时间t变化的数据，按y=lg(t+t0)/Δe与x=lg(t+t0)进行变换，在xy坐标系中，x较大的数据点将呈直线分布，则该直线斜率的倒数即为参数A，在y轴截距的倒数为参数Cα0.

2 试 验

利用改装后可测不排水面孔隙水压力的固结仪，对河南某地的黏性土进行了一系列向上单面排水的流变固结试验. 土样取土深度为2.5 m，相对体积质量ds=2.71，液限wL=39.4%，塑限wP=22.3%，塑限指数IP=17.1. 为保证土样均匀性，去除杂质后将其用蒸馏水进行充分浸泡，然后搅拌均匀后制成泥浆，最后采用泥浆静压法制备土样. 待土样成型后，参照GB/T50123—1999《土工试验方法标准》中的规定，利用高度为2 cm、内径为6.18 mm的环刀切取了一组饱和重塑土样. 经测定，试样密度为1.738 g/cm3，含水率为47.77%，初始孔隙比e0为1.30.固结试验中，取加荷比为1，最小和最大压力分别为25和1 600 kPa.

试验得到的不同荷载等级下试样的孔隙比e和不排水面(底部)处的孔压u随时间的变化情况分别示于图1，2. 从图1可以看出，不同荷载等级下孔隙比随时间变化曲线在出现“拐点”(即主次固结分界点)后，变形仍然持续发展. 这说明该类黏土具有较为显著的流变特点.

图2表明，不同荷载等级下的孔压并不是从加载时刻就达到外加荷载增量的，而是需经历一段时间才能达到峰值，随后进入消散过程. 该现象被称为“孔压滞后”现象[34-36]，其可能与试样饱和度、仪器内壁摩擦力、加载动力效应等因素有关. 同时，不同荷载等级下孔压峰值所对应的时刻并不相同.图2表明，随着荷载增量的增大，孔压达到峰值所用的时间也相应延长.另外，从图2还可以看出，当加载时刻达到图1中的“拐点”时，图2中相应时刻下的孔压还有相当一部分没有消散，这也说明该类黏性土具有明显的主次固结耦合特征. 因此，基于e-lgt曲线并按Casagrande法确定主次固结分界点的做法并不能保证过了该时刻后的变形全部是由流变引起的.为剔除主固结部分的影响，建议以孔压消散到一定程度(比如95%)对应的时刻作为主次固结分界点.

图1 孔隙比与时间的变化曲线

图2 试样孔压随时间变化关系

3 修正UH模型的验证

3.1 河南某地黏土

在上文中，对河南某地的黏性土在不同荷载等级下的流变固结特性进行了分析. 为验证修正UH模型的有效性，利用修正UH模型对上述试验结果进行了模拟. 模拟时，压缩指数Cc=0.42和回弹指数Cs=0.035是根据上述试验结果及其定义得到的；每级荷载等级对应的试样初始高度H0和初始孔隙比e0均根据上级荷载等级试验结束时的实测试样变形确定；黏土的有效内摩擦角按经验取为20°；非线性流变参数Cα0和A按照1.2节的方法作图拟合而得；初始超固结参数R0和渗透系数k根据试算选用. 具体参数值示于表1，模拟结果示于图3. 可以看出，修正UH模型能够较好地模拟本试验不同荷载等级下的变形过程.

表1 河南某地黏土分析所用参数

图3 孔隙比与时间的变化曲线

3.2 香港黏土

Yin[29]曾对香港地区的黏土进行过固结试验，部分实验数据见图4.据此，Yin给出了一个非线性流变的计算公式及相应EVP模型参数的确定方法.Le等[37]认为Yin[29]的方法在确定模型参数时有一定的局限性，因此，建议了TRRLS方法，其模拟结果见图4.本文按上述修正UH本构模型也对Yin[29]的试验数据进行模拟，所用参数见表2.其中，不同荷载等级下的试样高度H0、压缩指数CC=0.525、回弹指数CS=0.036 1、初始孔隙比e0均参考Le等[37]模拟所用参数取值，非线性流变参数Cα0和A根据Yin[29]试验数据按照1.2节计算方法获得，初始超固结参数R0和渗透系数k则根据试算选用，黏土的有效内摩擦角取为15°.模拟结果也示于图4.不难发现，本文修正UH本构模型也能够较好地描述香港黏土的流变固结特性.

表2 香港黏土分析所用参数

图4 竖向应变与时间的变化关系

3.3 萧山黏土

为进一步验证修正UH模型的适用性，本节对李西斌[38]的部分固结试验结果进行了模拟. 李西斌[38]的试验对象为萧山黏土，其中4组试样在荷载等级800～1 600 kPa下的的竖向变形S随时间t的变化曲线示于图5. 使用修正UH模型对其进行模拟时，4组试样的土性参数见表3.

表3 萧山黏土分析所用参数

其中，黏土的有效内摩擦角参考文献[25]取为25°，其他参数的选取方法同3.2节. 模拟结果示于图5. 很明显，修正UH模型能够较好地描述萧山黏土的流变固结特性.

4 结 论

1)次固结系数的时间效应是影响流变非线性过程的重要因素，考虑次固结系数的时间效应，对完善非线性流变本构关系具有重要意义.

2)次固结系数与时间对数的双曲线表达式(13)可以较好地描述黏性土的非线性流变特性.

3)基于次固结系数时间效应修正的UH本构模型可以较好地描述多地黏性土的一维流变固结过程，因而具有较广的适用性.