结合跳点引导的无人机随机搜索避撞决策方法

李安醍，李诚龙,*，武丁杰，卫鹏

1. 中国民用航空飞行学院 空中交通管理学院，广汉 618307

2. 乔治·华盛顿大学 机械与航空航天工程学院，华盛顿特区 20052

随着无人机技术的发展和世界城市化进程的推进，城市空中交通(Urban Air Mobility，UAM)的运输概念被NASA[1]、Uber[2]、Airbus[3]等机构重新提出。该交通方式旨在城市空域发展短程点对点运输系统，利用具有无人驾驶功能的垂直起降(VTOL)或短距起降(STOL)飞行器进行载人或载物运输以克服日益增长的地面交通拥堵问题[4]。但无人机在城市区域内执行运输任务将面临更复杂的空域环境，如部分高层建筑和限制飞行区域以及空中实时变化的密集交通流等因素将构成动态变化的障碍空间，而环境感知和避撞决策技术将是提供无人机在这种空间中穿行所需自动安全间隔保持能力的关键[5]。

城市空中交通的避撞问题结合了民航基于合作相关监视手段的避撞决策方法和移动机器人动态避撞路径规划的一般特性。相比于运输航空，城市空中交通流密度更大，飞行器需要在动静态障碍物中进行穿梭，且并不保证同一空域内飞行器都接受合作相关监视手段(广播式自动监视(Automatic Dependent Surveillance-Broadcast, ADS-B)、二次雷达)[6]；而相比于地面移动机器人，选择倾转旋翼(例如Airbus Vahana飞行器)等复杂气动布局飞行器在巡航飞行过程中较难实现长时间悬停，这意味着大多数飞行器必须在前飞过程中同时完成避撞机动。面向该应用场景，避撞决策算法不仅需要考虑无人机机载计算性能以满足实时机动决策的需要，还需考虑无人机本身动力学特性，尽可能优化避撞路径，使无人机整个运输过程安全高效。

文献[5, 7-8]对各类空中交通避撞建模与决策方法做了详细的总结和综述性工作，根据技术路线不同主要可将避撞方法分为3类：① 以几何方法为代表的被动式避撞决策，通过分析无人机和入侵对象几何空间位置相对运动速度矢量，进行飞行器危险接近最终阶段的冲突解脱[9]。对于飞行器间避撞问题较为有代表性的是最小接近点法(PCA)和碰撞锥法(CCA)[10-11]，这类方法计算简单，能够拓展到三维动态环境的飞行避撞问题上，但对多机避撞问题处理结果不够理想，所计算得到的避撞路径平滑程度得不到有效保障。文献[12]更多考虑了飞行器本身的机动性能，从最优控制理论角度给出了滚转角速度和法向过载的解析形式最优解，但该方法仍存在实时性不足的问题。② 基于无碰撞路径规划的主动避撞方法，即将避撞决策过程转化为带有安全间隔约束的无碰撞路径规划问题。其中人工势场法[13]在单机对静态障碍物避撞路径规划过程中，计算量小，具备机载部署所需的实时性，但容易陷入局部最优陷阱。文献[14]对传统的人工势场法进行改进，在斥力场表达式中乘上本机到目标地距离差因子，并将其他合作的无人机作为移动的障碍物进行计算，使得目标点位置能够成为全局力场的唯一最小值，很好地克服了人工势场法中路径规划的可达性和抖动性问题。文献[15]引入张量场概念将势场法拓展以解决4D航迹约束下的多机编队飞行避撞问题，但该方法仅在冲突发生时重规划，缺乏冲突的预测和事前调整，未考虑避撞对集群所带来的连锁反应，不适合无人机群体规模较大时的应用。文献[16-17]创新性地提出将无人机绕飞障碍物的轨迹以流水绕石现象进行建模，在路径规划过程中引入流体计算方法，其中解析法计算时间短，所规划的航路平滑且具有可飞性，但其对障碍物以球形边界划设保护区，对于不规则多边形障碍物乃至凹形保护区划设方式的避撞效果并未进行讨论和验证。针对空中多无人机交通流的合作式避撞问题，文献[18]提出了混合整数线性规划方法进行求解，甚至考虑了无人机冲突过程中的速度变化情形，但该方法随无人机数量增多时计算量会成几何倍数增加。③ 基于人工智能算法的避撞决策方法。早期的方法如A*算法[19]、蚁群算法[20]、遗传算法[21]能够解决无人机对静态障碍物避撞路径规划问题，其本质是用于路径规划的优化算法，考虑的避撞对象主要为静态障碍物，对于多无人机交通流避撞问题应用需要较多次迭代计算，实时性不够。近年来一些研究者开始将无人机避撞建模成多智能体决策问题[22-24]，从而便于利用强化学习等人工智能方法进行研究。Bai[25]和Mueller[26]等系统性考虑了无人机传感器测量误差等不确定性因素，并以部分可观马尔科夫决策过程(POMDP)进行建模，其中文献[25]采用蒙特卡洛数值迭代方法对三维连续状态空间进行求解，较好地解决了离散方法在应对高维状态空间过程中需要大量计算资源的问题。文献[26]主要讨论了如何自适应求解避撞过程中影响飞行器对间隔保持和轨迹跟踪之间性能的折中系数问题，拓展了部分可观马尔科夫决策过程建模解决避撞问题的通用性，但上述问题讨论的计算工作需要离线计算。受此启发，文献[27]应用马尔科夫决策过程(Markov Decision Process，MDP)对城市地区高密度交通流运行场景进行建模并采用蒙特卡洛树搜索(Monte Carlo Tree Search，MCTS)求解无人机避撞问题，该方法在实时性和避撞效果上取得了较好的效果，但其连续避撞飞行轨迹从全局来看并不是最优的，存在飞行器原位置盘旋的问题。

面对城市空中交通这一场景中同时出现的静态障碍和空中密集动态交通流，如何在保证算法实时性的前提下实现对动态障碍和静态障碍双重目标的自主避撞并优化避撞决策路径是本文研究的重点。本文将采用离散马尔科夫过程对空中避撞问题进行建模，基于Yang等[27]所提出的蒙特卡洛树搜索方法实时求解最优避撞动作，引入A*改进算法跳点搜索(Jump Point Search，JPS)进行起止点间全局路径规划，自动生成合适间隔的离散路径点以引导无人机进行更优的避撞动作选择，避开因搜索深度不足所导致的无人机陷入局部环境最优情形，从而在保证算法实时性前提下，实现了对障碍的避撞和飞行路径的优化，最终达到降低冲突概率和缩短飞行时间的目的。

1 背景知识

1.1 马尔可夫决策过程

马尔可夫决策过程最早由Bellman提出[28]，其后被广泛应用在机器人、自动控制、最优化等主题中，马尔可夫决策过程可用一个五元组表示为

其中：S为一组有限状态集；A为一组有限动作集；P为在时刻t对应状态St下采取动作a(a∈A)后转换到t+1时刻状态St+1的概率；R为通过执行动作a，状态St转换到St+1所带来的奖励，在本文中奖励值应符合R∈[0,1][29]；γ为折扣因子，表示未来的奖励在当前时刻的价值比例，即当前的奖励相对于未来的奖励能够获得更大的收益。

求解马尔可夫决策过程的关键在于找到一个执行策略。该策略是指从状态S到动作A的映射，即在给定状态下动作的概率分布，策略常用符号π表示为

π:S→A

最优策略π*，是指该策略能使得最终期望的总奖励值最大化，其表达式为

(1)

1.2 蒙特卡洛树搜索

蒙特卡洛树搜索算法是通过特定策略进行非对称树搜索的算法。搜索是一组沿着搜索树的遍历，单次遍历是从根节点到未完全展开的节点的路径，未完全展开的节点至少有一个子节点未被访问。在搜索过程中，算法并不会访问树的每一个分支，而是用搜索树上限置信区间(Upper Confidence bound apply to Tree，UCT)算法来寻找一个最佳的策略对树进行搜索[30]。UCT是将上限置信区间(Upper Confidence Bound，UCB)[31]运用到MCTS的算法。对于搜索树节点的选择既要给期望值高的节点更大的选择概率(Exploitation)，也要考虑探索那些暂时期望不高的分支节点(Exploration)。UCT算法通过各个节点的UCT值来决定访问哪一个节点，可以很好地权衡这种探索和利用(Exploration and Exploitation)。UCT算法公式为

(2)

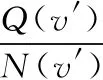
蒙特卡洛树搜索主要由选择(Selection)、拓展(Expansion)、模拟(Simulation)和反向传播(Backpropagation)4个阶段构成[32]。Selection阶段是在搜索树中寻找一个最有价值的节点，通常优先选择未被探索的子节点，否则选择UCT值最大的子节点。Expansion阶段是在当前选中的节点上进行一个随机动作并创建一个新的子节点。Simulation阶段是使上一个阶段中创造的新节点开始随机模拟的过程，直至达到终末状态。Backpropagation阶段是从叶子节点到根节点的遍历，并将Simulation阶段的模拟结果传送到根节点，对于反向传播路径上的每个节点，更新节点的回报价值、访问次数及其他有用统计信息。

1.3 跳点搜索

跳点搜索是A*算法的一种改进版本，其改进之处在于修改了A*算法的搜索规则，使得搜索速度最快能提高一个数量级[33]。A*算法是一种启发式算法[34]，拥有启发式函数H(n)以及两个列表：open列表和close列表，并用一个估值函数来评估节点的代价，估值函数的表达式为

F(n)=H(n)+G(n)

(3)

式中：G(n)为从搜索起始点到节点的实际代价；H(n)为搜索目标点到节点的估计代价。

A*算法首先从当前节点开始，将所有不在close列表的合法邻近方格放入open列表中。从open列表中选取F(n)值最小的方格作为下一个节点，并把当前节点移出open列表，放入close列表中。将选中的下一个节点作为当前节点重复上述步骤，直到目标点出现在open列表当中。

跳点搜索同样采用A*算法中的估值函数，但是不会逐一对邻近方格进行搜索，而是从当前节点开始沿着水平、垂直和对角线3个方向进行搜索。当搜索到转折点时，则把当前点移入close列表，并把转折点加入到open列表中。选取open列表中F(n)值最小的点，若此点为目标点则结束搜索，否则作为当前点并按上述步骤重新开始搜索。

2 建模与求解

美国洛杉矶市是Uber Air公司进行城市空中交通(UAM)验证飞行的试点城市之一。图1为大疆无人机公司在洛杉矶城市某空域划设的限制飞行区域，图中红色和灰色部分分别为禁飞区和限高区。从图中可以看出该空域的限制飞行区域会对无人机在城市空域下运行形成带状或凹形的静态障碍。

图1 限制飞行区域

针对Yang和Wei[27]未考虑到成片的高层建筑群或限制飞行区域对无人机在城市空域环境下运行的影响，本文在仿真场景中加入静态障碍，对无人机在静态和动态混合环境下的运行场景进行建模，并将场景之中的部分静态障碍设计为局部凹形，使其形成局部陷阱区域以增加环境复杂性。

2.1 场景与模型描述

假设无人机在城市空域下没有固定航路，而是按需自由飞行，城市空域高度层通常十分狭窄，因此无人机仅考虑在同一高度下进行水平机动避撞。本文将具有避撞算法的无人机称为试验机，没有避撞算法的无人机称为入侵机，用于模拟随机交通流形成的动态障碍。每次仿真实验，试验机将从固定起始点出发无碰撞地抵达随机生成的目标点位置，入侵机将以指定数量在模型中随机位置生成并以一定的初速度做匀速直线运动，模型不考虑入侵机两两之间的碰撞。

图2为仿真场景1(凹形限飞区空域)模型示意图，其模拟了边长为24 km含有凹形限飞区域的方形城市空域。模型缩放比例为1像素：30 m，那么该模型的大小为800像素×800像素。黄色带有环形的飞机图形代表具有避撞算法的试验机；红色飞机代表入侵机；绿色星形代表目标点；黑色图形代表由限制飞行区域形成的静态障碍。

图3为仿真场景2(含有凹形区域的多个限飞区空域)和仿真场景3(不含凹形区域的多个限飞区空域)的模型示意图，其缩放比例与图形代表的含义与图2保持一致。

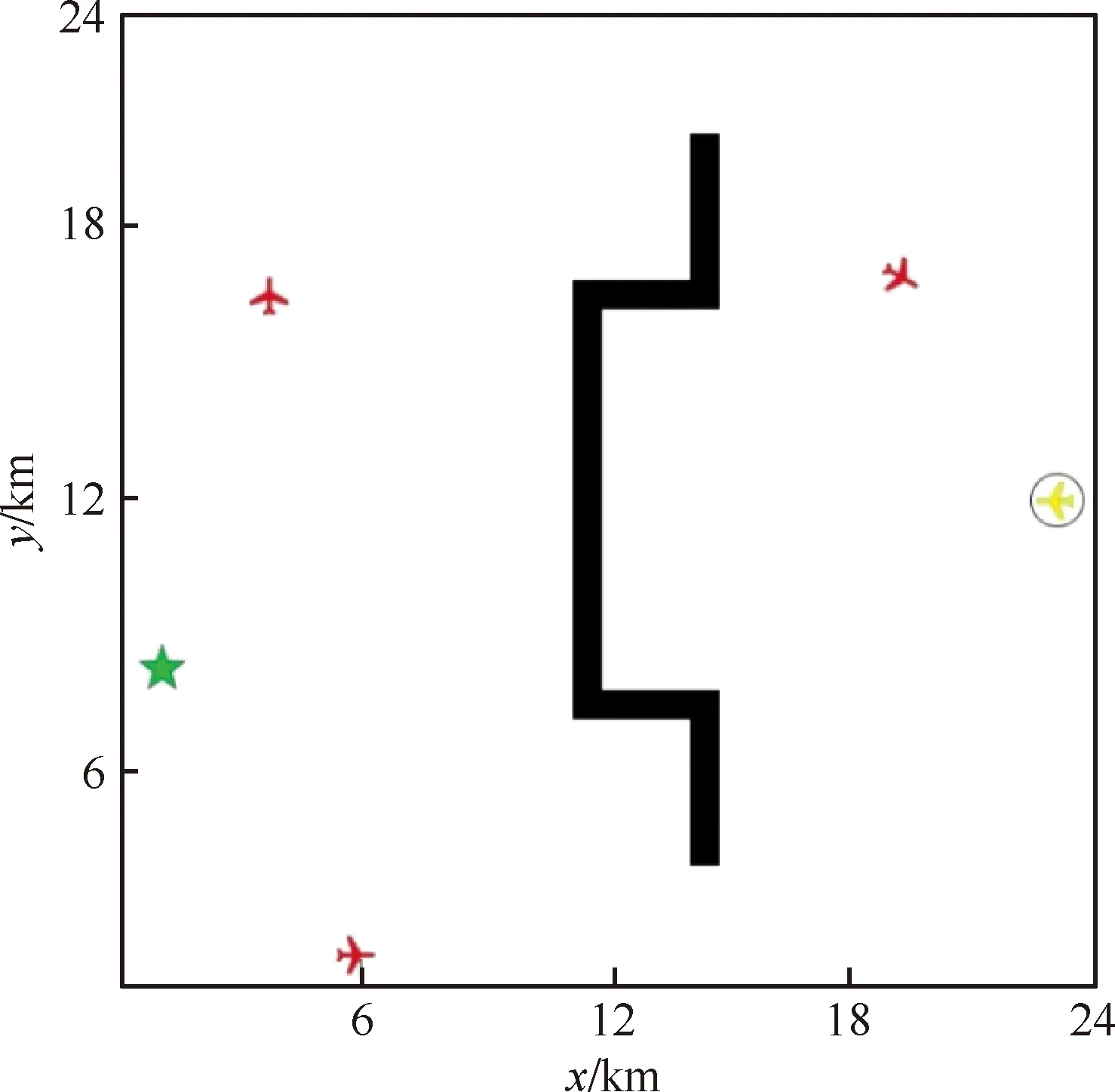
图2 仿真场景1模型示意图

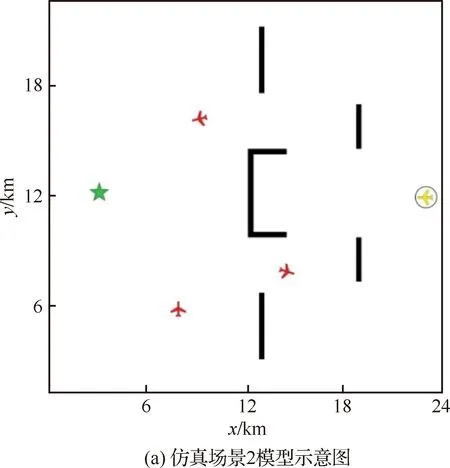
图3 限飞空域场景模型示意图

无人机之间的冲突与碰撞定义为

(4)

式中：ix、iy为入侵机位置的横纵坐标；ox、oy为试验机位置的横纵坐标；Δd为试验机与最近一架入侵机之间的距离；这里的碰撞指NMAC(Near Mid-Air Collision)[35]。

2.2 飞行器运动模型

无人机的运动学模型可表示为[27,36]

(5)

式中：ε为无人机运行过程中的不确定因素产生的噪声，其大小服从正态分布；Δt为时间变化量；v为无人机速度，且v∈[50,80] m/s；av为无人机加速度；εv为速度误差；φ为无人机倾斜角，且φ∈[-25°,25°]；εφ为倾斜角误差；aφ为倾斜角的改变率；θ为无人机航向角；g为重力加速度；x和y分别为无人机的横纵坐标；εx和εy分别为横纵坐标位置误差。

2.3 状态集描述

模型以1 s为单位进行离散化，并定义为一个时间步长t(time step)。这意味着无人机的速度、航向角度、位置等参数将以1 s为单位进行改变，利用式(5)并令Δt=1 s即可确定下一时刻无人机的各项参数。模型假设每5个时间步长(5 s)， 无人机将会做一次避撞决策，即从动作集中选取最佳的飞行动作。由于小型无人机通常具有极高的功率重量比，因此无人机动力学相对于5 s的决策周期是快速的[37]。

因为MDP需要执行一个动作后才进行状态转移，所以我们将模型中的状态空间以避撞决策频率，即5个时间步长为单位进行离散化，得到若干个中间状态S1,S2,…,Sn。每次仿真开始，试验机从初始时刻状态S0开始立即执行一次避撞决策并进入中间状态，在状态Sn的某时刻下触发终止条件则立即从中间状态转移到终末状态ST，因此完整的状态集为{S0,S1,S2,…,Sn,ST}。对于进入终末状态的终止条件

(6)

模型中，试验机的状态由坐标位置(ox,oy)、速度(ov)、航向角(oθ)4个变量表示；入侵机的状态由坐标位置(ix,iy)、速度(iv)、航向角(iθ)4个变量表示；目标点的状态由坐标位置(gx,gy)2个变量表示。设某时刻状态为St，若模型中有n架入侵机，那么状态St由(4×n+6)维状态分量组成，即

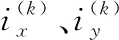
2.4 动作集描述

在真实环境中，无人机能在性能范围内选取任意的加速度和倾斜角进行机动。但是从连续的动作空间中选取一个最佳的飞行动作，对于MCTS其计算复杂度将成指数上升。为了简化计算，将模型中的动作空间离散为9维，由加速度动作子集和倾斜角动作子集组成有限动作集，动作集为

(7)

式中：Aa为加速度动作子集；Aφ为倾斜角动作子集；(av,aφ)为最优加速度和倾斜角的一个组合动作。

试验机每次执行避撞决策会从动作子集Aa和Aφ中通过MCTS选取一个最优加速度和倾斜角的组合作为当前的飞行动作。由于飞行动作有9种选择方案，所以MCTS所构建的树状结构最多有9d个节点，d为搜索树的深度。

2.5 奖励函数描述

避撞过程建模为马尔科夫决策过程后的原始奖励函数式为

(8)

式中：R(S)为在状态S时试验机在不同飞行条件下获得的奖励值;d(g)为试验机与目标点之间的欧式距离；max(d(g))为当前场景下，试验机与目标点之间所能达到的最大距离。

MCTS算法需要进行大量的随机过程模拟采样以获得最佳策略，所以将其应用于无人机避撞时，考虑到对算法实时性的要求，不可能进行长时间的运算来得到全局最优解，而只能在有限时间里得到当前状态下的一个局部最优解。因此，MCTS算法仅能满足短期内的局部冲突避撞。

原始的奖励函数仅计算试验机与目标点之间的欧氏距离，而为了获得最大的累计奖励值，MCTS算法选择的飞行动作是使得连线长度最短，因此，其期望航迹为试验机与目标点之间的连线。当试验机与目标点的连线之间存在静态障碍时，那么采取MCTS算法得到的飞行动作可能导致试验机的实际飞行航迹非全局最优，甚至陷入局部最优的陷阱之中，即无法抵达目标点。

无人机在城市环境中运行难免会因为地形因素或者限制飞行区域形成的静态障碍导致无人机无法直接到达目标点。MCTS算法能够满足对局部动态障碍避撞的要求，但是在城市空域下，无人机也需要同时对静态障碍进行避撞。对于静态障碍避撞的最优决策不是当无人机靠近静态障碍后再进行机动飞行避撞，而是应该规划一条无碰撞的最短路径并主动对静态障碍进行绕飞。因此，通过跳点搜索算法从全局规划出一条绕开静态障碍的路径并以合适的距离等间距建立路径点。无人机逐点飞行便可主动绕开静态障碍，并在两个路径点之间的飞行过程中，同时以MCTS算法选择飞行动作实现对局部动态障碍进行避撞。

考虑到目标点和路径点同时对航迹的影响，改进了原始奖励函数的表达式。改进后的奖励函数加入了路径点和试验机之间的距离因素，并通过比例系数来权衡目标点与路径点对试验机飞行动作的影响，使得无人机能对静态障碍主动进行绕飞并保持对动态障碍的有效避撞。试验机的期望航迹不再是一条简单的直线，而是由若干条线段组成近似曲线的线条。改进后的奖励函数为

R(S)=

(9)

式中：d(p)为试验机与最近路径点之间的距离； max(d(p))为当前场景下，试验机与路径点之间所能达到的最大距离；a为奖励函数的比例系数。

2.6 算法描述

为便于和原始的MCTS算法进行区分，本文将改进后的算法称作JPS-MCTS。首先通过程序创建一个名为Way Point的列表来存储路径点位置信息，在每次仿真实验中通过跳点搜索规划出一条避开静态障碍的最短路径后，将此路径按照合适的距离等间隔建立离散的路径点，并将路径点的位置信息加入Way Point列表。试验机遍历Way Point列表，从中选择一个与其距离最近的路径点，然后通过MCTS选择一个当前状态下所能获得最大奖励值的飞行动作并进入下一个状态，算法流程如图4所示。

图4 算法流程示意图

因为MCTS选择的动作是使得奖励值最大化，若试验机选择的动作能使得自身与路径点之间的距离缩小，那么试验机就能获得更多的奖励回报，其结果就是试验机飞向路径点。试验机到达路径点后，此路径点将从Way Point列表中移除，并重新选择一个与试验机距离最近的一个路径点。按照上述步骤，试验机将以一条优化过的航迹依次逐点飞行，并在飞行过程中同时实现对静态障碍和动态障碍的避撞。

3 仿真与结果分析

图5展示的是一次完整的仿真流程示意图，即从每次仿真开始时刻的初始状态S0到仿真结束时刻的终末状态ST

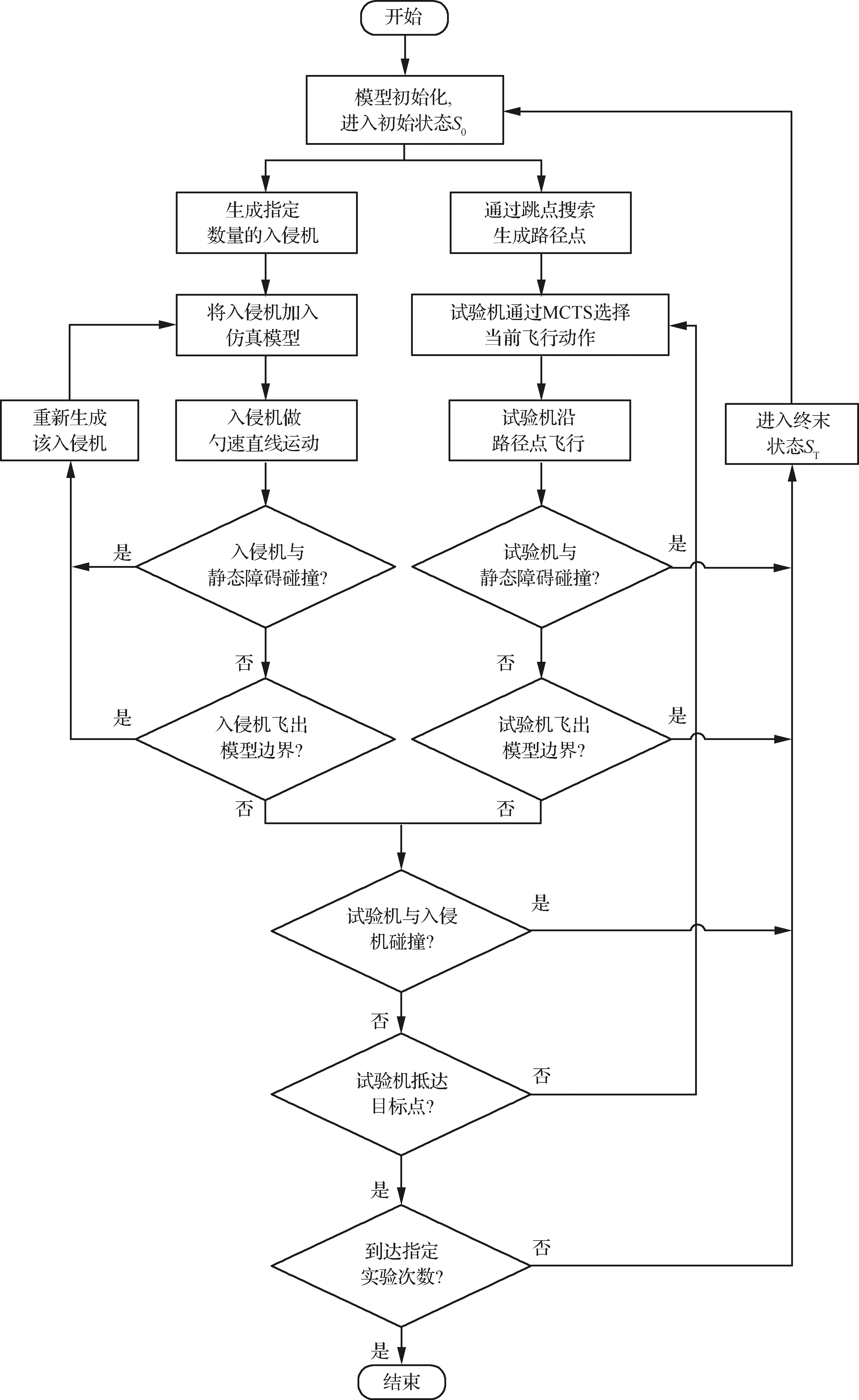
图5 仿真流程示意图

3.1 设置实验参数

本次实验采用的蒙特卡洛树搜索深度为3层， 随机模拟采样次数为100次。模型设置入侵机数量为60架，每个实验项目重复仿真500次，部分仿真画面如图6所示，蓝色实心圆点为引导试验机飞行的路径点。仿真中的各概率为

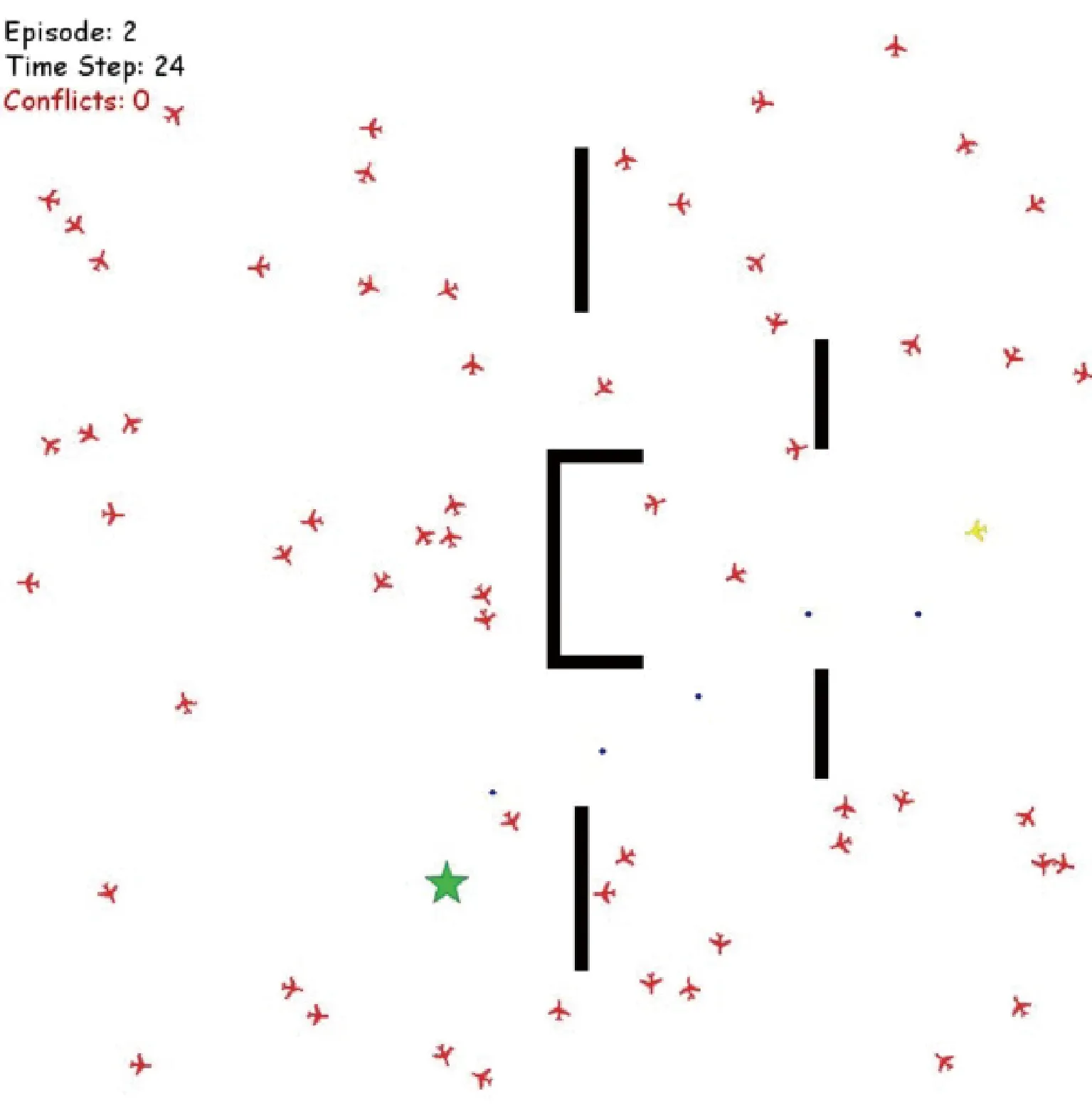
图6 仿真画面

(10)

式中：N为总仿真次数；Pn为NMAC概率；Pc为冲突概率；Pg为抵达目标点概率；Cn为NMAC的总次数；Cc为冲突的总次数；Cg为抵达目标点的总次数。

3.2 选取路径点的间隔距离

首先将奖励函数的比例设置为1.0，然后分别以40、60、80、100、120、140、160像素的距离等间距设置路径点并分别进行仿真实验，结果如表1所示。

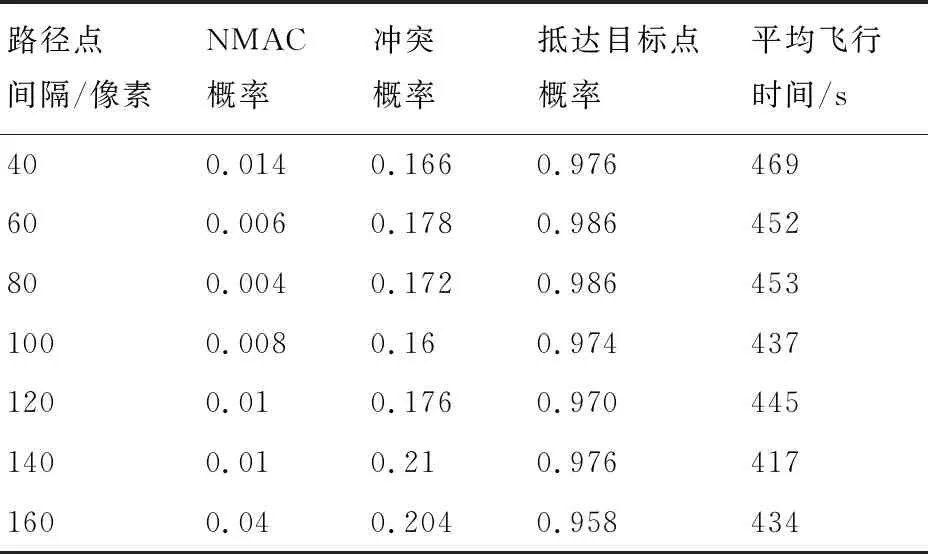
表1 不同间隔路径点条件下的仿真结果

对于无人机而言，安全性是最关键的要素，因此其性能参数首先应保证NMAC概率最小，其次是抵达目标点概率、冲突概率以及平均飞行时间。综合以上因素，这里选取80像素作为路径点的间隔距离，按照缩放比例换算成真实距离则是约2.4 km。

3.3 选取奖励函数的比例系数

首先将路径点的间隔距离设置为80像素，然后设置奖励函数的比例系数分别以1.0、0.9、0.8、 0.7、0.6、0.5、0.4进行仿真实验，结果如表2所示。

按照相同的原则，这里选取a=0.8作为奖励函数的比例系数。从表2仿真实验数据中可以观察到，不同的比例系数和不同间隔距离的路径点对飞行时间影响不大，而对于NMAC概率和冲突概率的影响较大。对于不同的比例系数来说，其平均飞行时间随比例系数减小而增加，这是因为比例系数越小，路径点对试验机的影响就越小，而目标点的位置对试验机干扰越大，这从侧面可以反映出原始的蒙特卡洛树搜索算法规划出的无碰撞航迹并不是最优的。

表2 不同比例系数条件下的仿真结果

3.4 对比实验

分别在仿真场景1、仿真场景2、仿真场景3中对原始的MCTS算法以及JPS-MCTS算法(间隔距离设置为80像素，比例系数a=0.8)进行仿真实验，仿真结果分别如表3～表5所示。

表3 仿真场景1结果对比

表4 仿真场景2结果对比

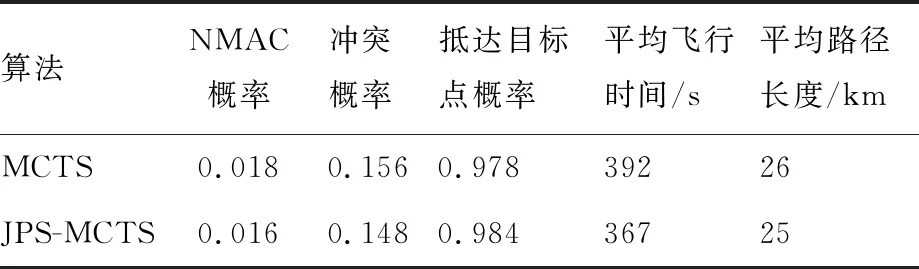
表5 仿真场景3结果对比

从表3中可以看出，对于“凹形限飞区空域”，JPS-MCTS算法相对于MCTS算法，NMAC概率降低了75%、冲突概率降低了36%、抵达目标点概率提升了40%、平均飞行时间缩短了47.8%、平均路径长度缩短了43.4%。

从表4中可以看出，对于“含有凹形区域的多个限飞区空域”，JPS-MCTS算法相对于MCTS算法，NMAC概率降低了75%、冲突概率降低了5.4%、 抵达目标点概率提升了5.4%、平均飞行时间缩短了15.9%、平均路径长度缩短了16.7%。

从表5中可以看出，对于“不含凹形区域的多个限飞区空域”，JPS-MCTS算法相对于MCTS算法，NMAC概率降低了11%、冲突概率降低了5%、抵达目标点概率提升了0.6%、平均飞行时间缩短了6.4%、平均路径长度缩短了3.8%。

从上述结果中可以看出，JPS-MCTS算法在场景1中的优势最大；JPS-MCTS算法在场景2中相对于场景3优势较为明显。场景1中的静态障碍是3个场景中对无人机阻碍范围最大的，并且场景1和场景2中都包含有凹形区域，因此可以推论出：JPS-MCTS算法在无人机需要对静态障碍进行大范围绕飞的场景中性能优势最为明显，对于含有凹形区域的场景其算法的稳定性也较好。原始的MCTS算法对于较大范围并含有凹形静态障碍的场景，其算法性能会出现明显下降。

同时，选取具有代表性的2个仿真场景：仿真场景1和仿真场景2，分别在仿真实验中将2种算法的冲突点位置进行记录，并绘制在地图上，结果如图7和图8所示。两图中的绿色圆点为发生冲突时试验机的位置，红色圆点为发生NMAC时冲突点的位置。从冲突和碰撞的散点分布可以看出，实验结果与预期一致。原始的MCTS求解避撞决策动作的算法容易陷入凹形区域且无法较好地实现对静态障碍物避撞。经过改进后的算法结合了全局路径规划和随机搜索避撞算法的优点，能够同时实现对静态障碍和动态障碍有效避撞，并避免无人机陷入凹形区域导致无法抵达目标点。改进后的算法由于其奖励函数通过权衡路径点和目标点的影响，使得无人机飞行路线更趋近于有人驾驶航空器的飞行路线，能够有效绕开静态障碍并且提高无人机到达目标点的效率，同时保留了随机搜索算法在避撞决策过程中实时性的优点。

图7 场景1中冲突点对比结果

图8 场景2中冲突点对比结果

4 结 论

本文针对城市空域环境下的无人机避撞问题展开了研究，提出了一种基于跳点搜索引导的避撞决策算法。该算法本质是将城市空间避撞问题进行解耦，针对先验的地形环境，应用跳点搜索预先建立最优离散路径点，结合这些离散路径点引导无人机在飞行过程中采用改进的具有较强实时性的蒙特卡洛树搜索算法解决试验机与动态障碍和静态障碍之间的避撞决策问题。相比于仅使用蒙特卡洛树搜索算法，改进后的算法在复杂空域环境中体现了全局规划的优势，能够对动态障碍避撞的同时对静态障碍实现主动绕飞并获得更优的飞行路线。在特定场景下，改进算法能够降低冲突碰撞发生的概率并且缩短飞行路程和飞行时间。

本实验场景着重讨论了复杂凹形静态障碍和密集交通流动态障碍共同影响下无人机避撞决策算法的性能表现。下一步将考虑在真实城市空域环境下进行建模仿真，用以测试该算法的通用性和实时性，并进一步对其鲁棒性进行探究。