BB84协议中测量转发攻击的侦测方法及其分析

卿 爽 陈小明,3

1(北京电子科技学院 北京 100071)2(西安电子科技大学通信工程学院 陕西 西安 710071)3(中国科学技术大学网络空间安全学院 安徽 合肥 230026)

0 引 言

在1984年由Bennett 和Brassard提出第一个量子密钥分发协议——BB84协议之后[1-4]，量子密钥分发在理论上成为了可能。近年来，量子密钥已经成为量子密码领域的研究热点[5-10]。量子密钥分发协议的安全性不同于传统密码算法所依靠的计算复杂度，而是基于量子力学基本原理来确保安全性，目前已证明量子密钥分发在理论上具有无条件安全性[11-16]。在实用的QKD工程中，协议中的原理都需要有相应的技术手段来落实，比如攻击行为的侦测问题，原理上有攻击和没有攻击的过程在收方数据的差错概率上会有显著区分，但我们看到的都是样本数据，在大样本前提下能得到概率的近似，最自然的方法是采用假设统计检验方法来判断是否存在攻击行为，但假设检验不可避免会导致弃真和取伪两类差错，从而引发安全和效率之间的矛盾。

本文通过分析测量转发攻击的技术过程提出采用假设检验来侦测攻击行为的方法，评估两类差错发生的概率。

1 量子密钥分发技术原理

目前大部分QKD技术使用BB84协议，有相位编码和偏振编码两种类型，本文以偏振编码协议为例进行论述。该协议是利用单光子的四种偏振态来对随机密钥信息进行编码，再对携带信息的单光子进行传输，每一个单光子所携带的信息都可以看作是1量子比特(Qbit)。在传输单光子的过程中，由“量子不可克隆定理”和“海森堡测不准原理”来保障BB84协议的安全性[17-20]。

图1为单光子的四个偏振态：水平偏振态|H>、垂直偏振态|V>、45°偏振态|+>和135°偏振态|->。|H>和|V>称为水平垂直基，简称为Z基。|+>和|->称为对角基，简称为X基。

图1 四种单光子偏振态

在BB84协议中，发送方Alice随机选取四种偏振态对待传输的密钥信息进行编码，经量子信道将这些包含密钥信息的量子态发送给接收方Bob；Bob在接收到这些量子态对每个量子态随机选取X基或Z基进行测量。测量完成之后，Alice和Bob通过公共经典信道来交换他们的基选择信息，若双方对于同一个量子态的制备基与测量基选择是一致的，就保留这份数据，反之则舍去这份数据，这一过程称之为基矢对比。而后Alice从保留的数据中选取部分(例如50%)用于侦测是否存在测量转发攻击，Alice将选中的数据公开，Bob根据将其与自己所测量到的数据进行对比来计算响应的误码率，若误码率过高则说明存在窃听行为，双方可以终止本轮协议重新开始。若误码率在合理范围内，Alice和Bob将进数据后处理，包括数据协调、保密增强等步骤，最终双方得到一段安全密钥。图2为使用BB84协议产生密钥的过程。

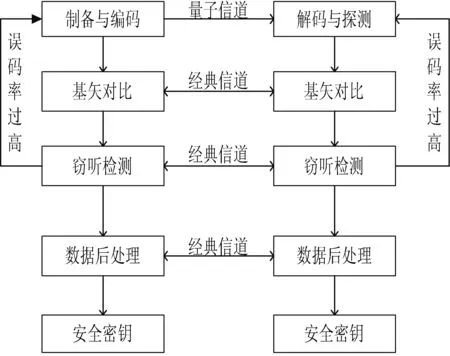
图2 BB84协议流程图

2 测试转发攻击过程及分析

发送方Alice和接收方Bob在进行量子密钥分发的过程中不仅使用了量子信道，还使用了经典信道，量子信道用于传输携带量子态信息的光子，经典信道用于双方进行基矢对比。经典信道是完全公开的，Alice和Bob的所公布的制备基和测量基信息可以被任何人接收到，但这些信息与密钥信息无关，并不会影响到整个协议的安全性。

窃听者Eve实施攻击的具体过程如下：

(1) 在Alice随机选取两组长度相同的序列{xn}和{an}，其中{xn}决定选取哪种基，{an}决定发送该基下的哪一种偏振态。{an}即为随机密钥序列。

(2) Alice完成量子态的制备后发送给Bob时，Eve在量子信道中截取Alice所发送的量子态，并随机选取一组测量基{zn}对每个量子态进行测量，测量结果记为{En}。而后Eve根据{zn}和{En}来制备相应的量子态发送给Bob。

(3) Bob在接收到Eve发送给他的量子态之后，随机选取一组测量基{yn}进行测量，测量结果记为{Bn}。

(4) Alice通过一个公共的经典信道公布其制备基选择{xn}，Bob将其与自己的测量基{yn}进行对比，将两者相同的位置通过公共信道告诉Alice，双方保留相同的位置所对应的量子态信息，舍弃不同的部分。

(5) Eve同样可以从公共信道获取到Alice和Bob进行基矢对比的信息，因为他可以保留与Bob完全相同的量子态，从而达到窃听的目的。

在Eve实施攻击的过程中，由于量子不可克隆定理，Eve无法完美克隆这些量子态而不引起扰动，即Eve在对Alice制备的量子态进行测量的过程中，若使用了与制备基不同的测量基进行测量，量子态将塌缩成该测量基下的随机一种偏振态。因此Eve无法得知自己是否选对了测量基，即使Eve选择了错误的测量基，也只能根据这个错误的基组来制备量子态发送给Bob。

理论上来看，由于Eve是随机选取测量基的，因此她将会有一半的测量基选择不正确，从而导致其发送给Bob的量子态中有一半是错误的。在测量这一半错误的量子态信息时，若Bob选择的测量基与Eve的测量基不同(即与Alice的制备基相同)，则Bob所测的量子态将会等概率随机塌缩成该基下的一种偏振态。因此，对于Eve转发的一半错误量子态，Bob仍有50%的概率测得与Alice所发的正确的量子态信息。从整体上来看，Alice和Bob在双方基选择都正确的情况下，测量转发攻击仍会导致通信双方存在25%的误码率。

由上述分析可以得出，若Eve实施了测量转发攻击，根据量子不可克隆原理，攻击行为将会使Bob端产生25%的误码率，这与没攻击行为时接近于0的误码率是十分容易区分的。但在实际应用BB84协议进行量子密钥分发时，概率不能直接显现，只能通过样本数据来进行检验，即使用频率来代替概率。Eve的窃听行为所造成的误码率并不是严格等于25%，其数值应该在25%附近波动，极端的状况下Eve完全可能选到与Alice和Bob一样的测量基，从而Bob从差错率上完全无法感知到攻击行为的存在。因此，在实际操作中如何判断此次通信是否遭到窃听便成为非确定性问题，本文考虑利用统计学中假设检验的方法来进行判断。假设检验必将导致两类差错的产生，引发安全性与效率之间的矛盾。

3 差错概率分析

在m重伯努利实验中，事件A发生的概率为p(0

(1)

则有Yn～N(0,1)。由此可得n～m(mp,mp(1-p))，即n服从均值为mp、方差为mp(1-p)的正态分布。

(2)

(3)

(4)

若u落在拒绝域内，则拒绝原假设H0，反之则接受原假设H0。同时也可以由拒绝域计算出被检测值的1-α置信区间为：

(5)

即每次检测的误码率以1-α的概率落入该区间内。显著性水平α为犯第一类错误的概率，也就是把存在攻击错判为无攻击情况的概率。β为犯第二类错误的概率，也就是把不存在攻击判断为存在攻击的情况。在样本量给定的条件下，α与β中一个减小必导致另一个增加。

表1 几种显著性水平与对应的置信区间

由于α和β的大小是相互影响的，因此无法同时控制二者，在密钥分发的过程中，犯第一类错误所产生的后果远比第二类错误要严重，且β不易求出。故本文选择控制α来使检验犯两类错误的概率达到一个合适的平衡。由表1可以看出，当置信区间为(21.03%，28.97%)时，α的大小是可接受的，且此时不会因α过小而导致β太大。若继续扩大置信区间，将系统误差所产生的误码率判定为攻击行为的概率就会提高，使得密钥分配效率下降。因此，在实际应用QKD系统中，使用1 800位数据进行窃听检测，当误码率超过21.03%时，即认为此次通信有99.99%的概率存在窃听。

4 结 语

本文通过使用假设检验的方法对BB84协议中因测量转发攻击而引起误码率变化的问题进行了分析，通过理论上的公式推导给出了较为详细的判别方法，并对数据进行了实际分析。实际上，假设检验并不能给出一个完全确定的结论，只能说明在相当大的概率下是服从原假设或备择假设的，但总有小概率的情况犯两类错误。在窃听检测中，第一类错误是把有窃听检测成无窃听；第二类错误是把无窃听检测为有窃听，后者的严重性要远超前者。本文选择控制犯第一类错误的概率，是因为第二类错误的概率不易求出，但二者是息息相关的，故可以通过控制第一类错误的概率来使窃听检测环节的结论更加可靠。本文主要分析的是测量转发攻击，但在量子密钥分发技术的实际应用中需要面对的攻击远不止这一种，因非窃听行为而产生的误码原因也有很多。本文以简化的密钥分发过程为基础，为将来考虑到复杂环境、多种攻击的误码率分析指出了方向，例如在不完美光源而产生多光子的问题中窃听者采取PNS攻击[21]而产生的误码率。