基于部分补偿干涉的非球面顶点曲率半径加工误差测量

胡 摇， 李腾飞， 郝 群， 常 旭

(1.北京理工大学光电学院精密光电测试仪器及技术北京市重点实验室，北京100081；2.中国北方车辆研究所，北京100072)

1 引 言

非球面光学元件广泛应用于各种光学仪器中，用来改变光路、校正像差、改善像质、减少光学系统的体积和重量[1，2]。特别是在天文望远镜，外太空望远镜和卫星遥感相机领域，高精度的非球面起着十分重要的作用[3，4]。

非球面的加工误差可以分为两类：面形误差(surface figure error，SFE)和面形参数误差。面形误差是被测面与标称面之间的不规则偏差，可以通过干涉仪[1]和轮廓仪[5]进行测量；面形参数误差包括顶点曲率半径加工误差和二次常数加工误差。其中，顶点曲率半径(vertex radius of curvature，VROC)加工误差是指非球面的实际顶点曲率半径与理想值之间的偏差，它影响非球面的基本性质，比如非球面的焦距，进而影响光学系统的像差和成像质量。精确测量非球面的顶点曲率半径加工误差对光学面的加工制造和校准是非常重要的，一直以来是研究的热点问题。

作为参考，传统的球面曲率半径测量方法是“猫眼和共焦位置”法，即通过自准直或干涉条纹判读法来精确定位猫眼位置和共焦位置两点，并测得这两点之间的距离来获得曲率半径[5，6];而非球面的几何关系较为复杂，通常很难直接找到其共焦位置，为顶点曲率半径加工误差的测量带来一定的困难。按照是否接触被测面，非球面顶点曲率半径加工误差的主要测量方法可以分为两类：接触式测量方法和非接触式测量方法。

接触式测量方法是利用轮廓仪[5，7，8]和三坐标机[9～12]，对被测非球面进行逐点测量，通过曲面拟合计算其顶点曲率半径，进而与理想值比对计算加工误差。但是，该方法容易受到扫描非正交性的影响，引入较大的系统误差[13]。测量仪器接触被测面，一般情况下要求被测面进行抛光处理；在测量过程中，测量仪器和被测非球面均会因挤压而产生磨损和变形，影响测量结果；对环境要求高，静电、灰尘和震动等均会使测量精度降低[8，13，14]。

非接触式测量方法不会造成被测面的损伤，测量结果精度较高，受到越来越多的关注。进一步对非接触式测量方法进行细分，包含非干涉测量方法与干涉测量方法两大类。对于非干涉测量方法，一种常用的方法是使用激光扫描轮廓仪[15]来获得被测面的顶点曲率半径加工误差，其相对测量精度可以达到0.02%。哥伦比亚国立大学的Mejía等基于哈特曼光阑检验[16]，提出了一种Null screen方法来测量二次曲面的顶点曲率半径加工误差[17]，相对测量精度可以达到0.15%，但是该方法存在Null screen只能测量某一个特定类型的非球面的问题，导致其动态测量范围较窄;普埃布拉州立大学的Diaz-Uribe[18，19]、清华大学王浩[2]和中国科学院光电技术研究所的黄传科[20]等基于法线像差的几何性质，进行非球面顶点曲率半径加工误差的测量，相对测量精度可以达到0.5%。这类方法的原理均较为简单，但是由于仪器和设备的制约，相对测量精度或者测量范围受到一定的限制。

对于干涉测量方法，一般是通过零位补偿干涉来获得非球面的顶点曲率半径加工误差[21，22]。汉茨维尔阿拉巴马大学的Robinson等通过零位干涉系统获得的相对测量精度优于0.1%[23]；但是，一种零位补偿器或者零位全息图(computer generated hologram，CGH)只能测量某一个特定类型的非球面，测量范围窄，周期长，开发成本较高。而基于部分补偿干涉(partial compensation interferometry，PCI)的非球面测量可以在提高相对测量精度的同时拓宽测量范围，具有较广的应用前景；然而，传统的PCI系统只能测量非球面的面形误差，无法获得非球面的顶点曲率半径加工误差。目前，仅有浙江大学杨甬英等提出了一种基于部分零位干涉的非球面顶点曲率半径加工误差测量方法[24]，使用部分零位干涉系统的多重结构模型进行同步优化，同时获得被测非球面的顶点曲率半径加工误差和面形误差，其相对测量精度可以优于0.025%；该方法使用的干涉系统多重结构模型，可能会导致波前相位的测量逐渐积累误差，最终影响整个系统的测量精度。

本文首先针对PCI系统中顶点曲率半径加工误差与面形误差的耦合问题，提出旋转对称非球面的误差分离原理，从而消除面形误差中耦合的部分顶点曲率半径加工误差；然后，在分析PCI系统的剩余波前像差的基础上，建立初级球差项与顶点曲率半径加工误差的关系；最后，提出一种基于PCI的非球面顶点曲率半径加工误差测量方法，在简化测量系统结构的同时，实现非球面顶点曲率半径加工误差的高精度测量。

2 基本测量原理

2.1 部分补偿干涉法的原理

光学系统中用非球面光学元件可以在增强像差的同时减少系统中光学元件的数量。但是如果将非球面光学元件和它所属的系统分开，那么在进行非球面检测时，该元件会产生非球面波前;而在干涉系统中，非球面波前与参考波前干涉的条纹密度很可能超过探测器的分辨率，因此非球面波前自身的检测要比球面波前或者平面波前较困难[16]。

零位补偿干涉法通过使用零位补偿器把非球面波前完全转化为球面波前或者平面波前，然后与参考波前进行干涉，对其结果进行分析计算，即可获得被测非球面光学元件的相关信息;PCI法则使用部分补偿器减小干涉系统剩余波前的最大斜率，使得干涉条纹的密度满足探测器分辨率的要求[25]，同时具有较高的精度、较大的动态范围和一定的通用性。

PCI法用于非球面面形误差测量的原理如图1所示，包括1台实际干涉仪以及1台通过计算机建立的虚拟干涉仪，PC是部分补偿器(partial compensator)。在实际干涉仪中，采用实际PC补偿被测非球面，从而得到包含被测面误差信息的一幅实际干涉图；在计算机中，根据实际干涉光路，在被测面位置虚设与被测非球面对应的标准非球面，并代入已知的PC参数，用光线追迹的方法得到4幅移相虚拟干涉图。采用数字莫尔移相干涉技术比较处理实际干涉图与虚拟干涉图，即可得到被测非球面的面形误差信息[3，26]。

图1 部分补偿干涉法原理图Fig.1 Schematic diagram of partial compensation interferometry

对顶点曲率半径加工误差测量而言，与零位补偿干涉系统不同，PCI系统不存在零位置，无法确定实际被测面和虚拟被测面的相对位置，使部分顶点曲率半径加工误差信息被离焦补偿而丢失，而无法直接获得非球面的顶点曲率半径加工误差;同时顶点曲率半径加工误差与面形误差耦合。为有效分离2种误差，并发挥PCI方法的优势，基于PCI本文进行了非球面顶点曲率半径加工误差测量的研究。

2.2 误差分离原理

该原理的目的是将顶点曲率半径加工误差剔除，得到完整的面形误差信息。光学系统中通常采用的是旋转对称非球面，在直角坐标系中，设Z轴为非球面的旋转对称轴，非球面的顶点P与坐标原点重合，可以建立非球面的曲面方程，用以表征非球面的面型，其关系式可表示为[16]：

(1)

式中：S2=x2+y2；|S|表示非球面上任意一点到旋转对称轴的径向距离；R0是非球面的顶点曲率半径；K0是二次曲面常数，K0=-e2，e为二次曲面的偏心率；A2i是高次非球面系数。

对式(1)进行麦克劳林级数展开(McLaurin series expansion)，可以获得：

(2)

式中D2i为非球面形变系数。

2.3 非球面顶点曲率半径加工误差测量的原理

在获得去离焦面形误差的基础上，研究剩余波前像差的初级球差项与顶点曲率半径加工误差的关系，可以得到基于PCI的非球面顶点曲率半径加工误差测量方法。

首先，对PCI系统的剩余波前像差进行研究。图2为部分补偿干涉系统测量臂的结构示意图，SUT表示被测非球面(aspheric surface under test，SUT)；剩余波前经由理想透镜汇聚在像平面处，然后与参考球面波干涉形成部分补偿干涉图。

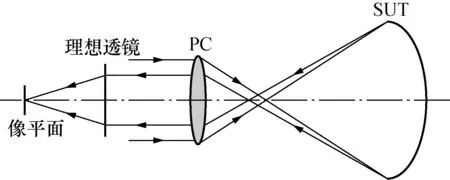
图2 部分补偿干涉系统测量臂结构示意图Fig.2 Sketch map of the measured arm of the partial compensation interferometer

在PCI系统中，SUT的球差并没有被完全补偿，存在部分余量，从SUT处反射的光线不沿原路返回，剩余波前为非球面波前，系统存在一定的剩余波前像差。当沿光轴方向移动SUT时，剩余波前的分布会发生变化，即系统会产生额外的剩余波前像差，且种类与原剩余波前像差一致，不会产生新的像差分量。鉴于PCI系统是以补偿球差为主，这里只考虑剩余波前像差中的球差分量，将其变化量记为ΔWS(Δl)，其中Δl是SUT沿光轴方向的位置变化量，其关系可以表示为[27]：

(3)

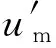
为了便于分析和研究，需建立Zernike初级球差系数与Δl的关系。一般用Zernike多项式的前九项表示初级像差，对其进行合并同类项和等价替换，可以得到球差分量的变化量表达式：

ΔWS(Δl)=6·ΔZ8·S4

(4)

式中：ΔZ8是Zernike多项式的第9项系数的变化，可以用来表示初级球差的变化。

可知，ΔZ8与Δl成正比[27]，则Z8随SUT沿光轴方向的位移满足直线关系：

Z8(Δl)=k·Δl+b

(5)

式中：k和b分别是直线的斜率和截距。

然后，对初级球差项Z8与顶点曲率半径加工误差ΔR的关系进行研究。构造4种不同的SUT形式用于像差分析。

(1) 实际SUT：同时包含去离焦面形误差和顶点曲率半径加工误差，记为SR，其剩余波前的初级球差用Z8R来表示；

(2) 虚拟SUT：只包含去离焦面形误差，记为SF，其剩余波前的初级球差用Z8F来表示；

(3) 构造SUT：只包含顶点曲率半径加工误差，记为SC，其剩余波前的初级球差用Z8C来表示；

(4) 理想SUT：不包含任何加工误差，记为SV，其剩余波前的初级球差用Z8V来表示。

如果沿光轴方向移动SR、SF、SC和SV相同的距离Δl，根据式(5)，Z8R、Z8F、Z8C、Z8V的数值变化均满足直线关系，则Z8R-Z8F和Z8C-Z8V也是直线，记Z8R-Z8F=Z8RF，则有：

Z8RF=kRF·Δl+bRF

(6)

式中：kRF和bRF分别是直线的斜率和截距。

同理，记Z8C-Z8V=Z8CV，则有：

Z8CV=kCV·Δl+bCV

(7)

式中：kCV和bCV分别是直线的斜率和截距。

大量仿真实验结果表明：式(6)和式(7)表示的两条直线具有较好的平行关系，即kRF≈kCV；而kCV与非球面顶点曲率半径加工误差ΔR近似成正比，即

kCV=α·ΔR+β

(8)

式中：α是比例系数；β是直线的截距。在系统结构确定后，无需实际被测面即可通过光学设计软件进行预先标定。

因此，利用包含实际SUT的实际PCI和包含理想SUT的虚拟PCI系统1采用数字莫尔移相干涉测量得到的结果，以及包含虚拟SUT的虚拟PCI系统2模拟得到的结果，即可拟合得到式(6)所示直线和kRF；根据kRF≈kCV以及预先标定得到的α和β，利用式(8)，即可求得实际SUT的顶点曲率半径加工误差ΔR。

3 系统结构与测量流程

建立图3所示的基于PCI的非球面顶点曲率半径加工误差测量系统框图，使用虚拟PCI系统1和实际PCI系统来测量实际SUT(即SR)位于光轴不同位置时的剩余波前像差，使用虚拟PCI系统2来获得虚拟SUT(即SF)位于光轴不同位置时的球差Z8F，具体测量流程为：

(1) 确定补偿镜和被测镜名义参数后，预先建模构造SUT，标定求解kCV与ΔR的关系，计算其比例系数α和截距β；

(2) 基于PCI法和误差分离原理，获得实际SUT的去离焦面形误差；

(3) 利用虚拟PCI系统1和实际PCI系统，通过数字莫尔移相干涉技术，计算实际SUT(包含面形误差和顶点曲率半径加工误差)位于光轴不同位置Δl时的剩余波前球差Z8R；

(4) 利用虚拟PCI系统2，获得虚拟SUT(包含去离焦面形误差)位于光轴不同位置Δl时的球差Z8F；

(5) 计算Z8R-Z8F，对其与Δl关系进行拟合，计算斜率kRF，利用kRF≈kCV获得kCV；

(6) 利用式(8)计算实际SUT的顶点曲率半径加工误差ΔR。

图3 基于PCI的非球面顶点曲率半径加工误差测量系统框图Fig.3 Diagram of fabrication error measuring system for the VROC of aspheric surface based on PCI

4 实验验证

在第2.3节阐述的测量原理中，ΔZ8与Δl成正比是严格满足的，但式(6)和式(7)表示的两条直线具有较好的平行关系，即kRF≈kCV是近似关系，且式(8)所示线性关系也是近似的，因此有必要通过仿真实验验证上述原理的精度和可行性。

利用ZEMAX对基于PCI的非球面顶点曲率半径加工误差测量法进行验证，理想非球面参数：R0=1 179.45 mm，D=580 mm，K0=-0.499 4，非球面度107.1λ，激光器的波长为550 nm。仿真实验中，实际PCI系统也由ZEMAX软件仿真完成。以Zernike多项式的形式来向实际SUT添加面形误差，其值为：第5项至第18项和第20项系数10-4，相应的分布如图4所示。向实际SUT添加的顶点曲率半径加工误差为1.54 mm，即实际SUT的顶点曲率半径为1 180.99 mm。

图4 向实际SUT添加的面形误差分布Fig.4 The distribution of surface error added to the real SUT

首先，求解kCV与ΔR的关系，结果如图5所示，其比例系数α=0.475 5，截距β=0.003 2。

图5 kCV与ΔR的关系Fig.5 The relationship between kCV and ΔR

其次，分别将实际SUT和虚拟SUT置于光轴的不同位置Δl，共取相隔0.5 mm的9个采样点，计算其剩余波前球差Z8R和Z8F。

然后，计算Z8R-Z8F，并对Z8RF和Δl的关系进行拟合，结果如图6所示，斜率kRF=0.740 5。

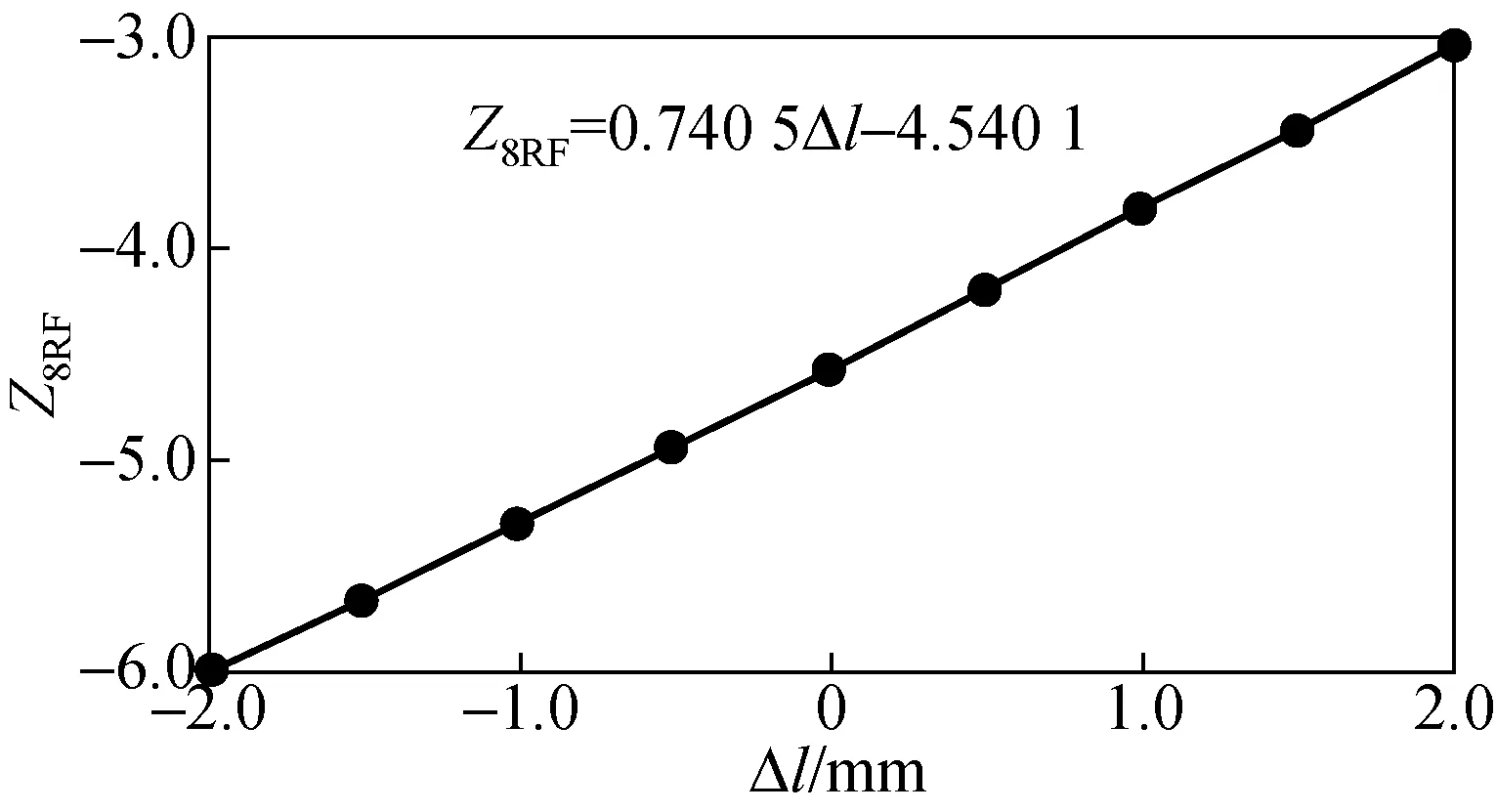
图6 Z8RF和Δl的关系Fig.6 The relationship between Z8RF and Δl

最后，kCV=kRF=0.740 5，根据式(8)，计算实际SUT的顶点曲率半径加工误差ΔR=1.56 mm。

对比引入顶点曲率半径加工误差真值1.54 mm，结果的相对测量精度为(ΔR-1.54)/R0=0.002%。

向非球面添加不同的顶点曲率半径加工误差，可以得到如表1所示的结果。

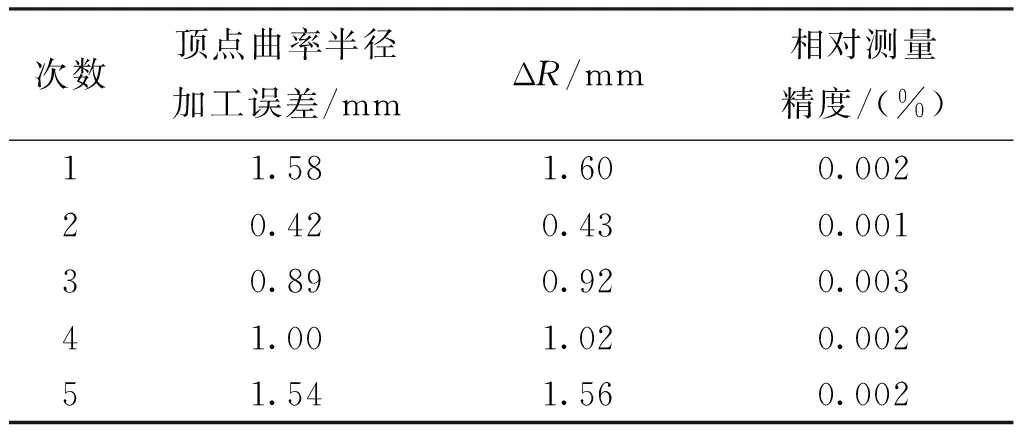
表1 不同顶点曲率半径加工误差的测量结果Tab.1 Measuring results of VROC fabrication error

5 结 论

针对当前部分补偿干涉法中缺少顶点曲率半径加工误差测量方法的现状，本文提出一种基于部分补偿干涉的非球面顶点曲率半径加工误差测量方法，以部分补偿干涉系统的剩余波前像差为切入点，对其进行分析和研究，得到了初级球差项与顶点曲率半径加工误差的关系，进而实现顶点曲率半径加工误差的高精度测量。

该方法的原理相对测量精度仿真结果优于0.003%，实际测量时其限制因素包括：(1) 测量过程中的曲面拟合、Zernike多项式拟合和直线拟合引入的误差；(2) 系统测量误差，如面形误差测量偏差和实际被测非球面沿光轴方向的位移偏差等；(3) 环境因素的干扰，如光学平台的振动、大气扰动等。对上述误差源进行限制和校准，可以进一步提高非球面顶点曲率半径加工误差的相对测量精度。