单车共享下城市居民出行方式选择行为模型分析——以湛江市为例

李 曼

(岭南师范学院机电工程学院，广东 湛江 524048)

1 出行方式选择模型的分析

1.1 模型构建

非集计模型的构建来自于出行者出行过程，其包括许多变量，成本低、效率高、可替代性强，在交通运输等领域得到普遍的研究和运用。本文以广东省湛江市为例，分析在共享单车的引入下城市居民的基本出行特征。为了较为准确的获取湛江市居民出行基础数据，选取5个交通大区为代表性的出行区域。依据行为理论，制定了“湛江市居民出行调查问卷”，并遵循交通调查方法和原则进行实地调查。调查总共发放问卷5 000份，收回4 843份，有效问卷4 759份。其中从有效数据中随机抽取2 039份，利用非集计理论构建模型。

依据效用最大化理论，即假设出行者n选用第i中出行方式的效用为Uin，选用第j种出行方式的效用为Ujn，An为出行者n出行方式的选择方案集合，则出行者n选择出行方式i的条件如式(1)。

Uin>Ujn,i≠j,j∈An

(1)

其中Uin可以表示为式(2)

Uin=Vin+εin

(2)

式中：Vin为出行者n选择第i种出行方式的效应函数中固定效用部分；εin为出行者n选择第i种出行方式效应函数中随机效用部分或者随机误差项。

若Vin与特性向量Xink呈线性关系，则其关系如式(3)

(3)

式中：K为特性变量的个数；θk第k个变量对应的参数；Xink为出行者n选择第i中出行方式的第k个特性变量。

假设上式中Vin与εin相互独立，并且εin服从二重指数分布，则出行者n选择第i种出行方式的概率Pin可用式(4)描述：

(i,j∈An)

(4)

1.2 交通方式选取及影响因素划分

湛江市居民出行方式复杂，居民出行方式包含公交车、出租车、私家车、摩托车、电动车、单车以及步行等多种交通方式，其中为了简化研究，把出租车和私家车归为一种交通方式——即小汽车，故湛江市居民出行方式以步行、摩托车/电动车、公交车、小汽车和单车为主。其中单车方式中单车来源包括家庭拥有单车和共享单车。那么，模型的选择肢可定义为：步行、电动车/摩托车、公交车、小汽车、单车，分别用0、1、2、3、4表示。

经初步筛选、归类、分组后，选取的影响因素包括两部分构成，个人属性、家庭属性和出行属性。个人属性包括性别、年龄、教育程度、个人月均收入等4个参量，家庭属性包括拥有小汽车情况、拥有摩托车/电动车情况、拥有单车情况、具备共享单车使用条件等4个参量，其中具备单车使用条件参量定义为只要满足具有共享单车年卡或者手机上安装有单车APP并注册会员的其中一个条件，即可取值为1；出行属性包括出行距离、出行目的、出行时间、出行费用等4个参量，其中出行费用主要是指乘车费用。具体影响因素见表1。

表1 影响因素说明

1.3 模型参数的标定与分析

对模型影响因素进行标定，结果见表2。

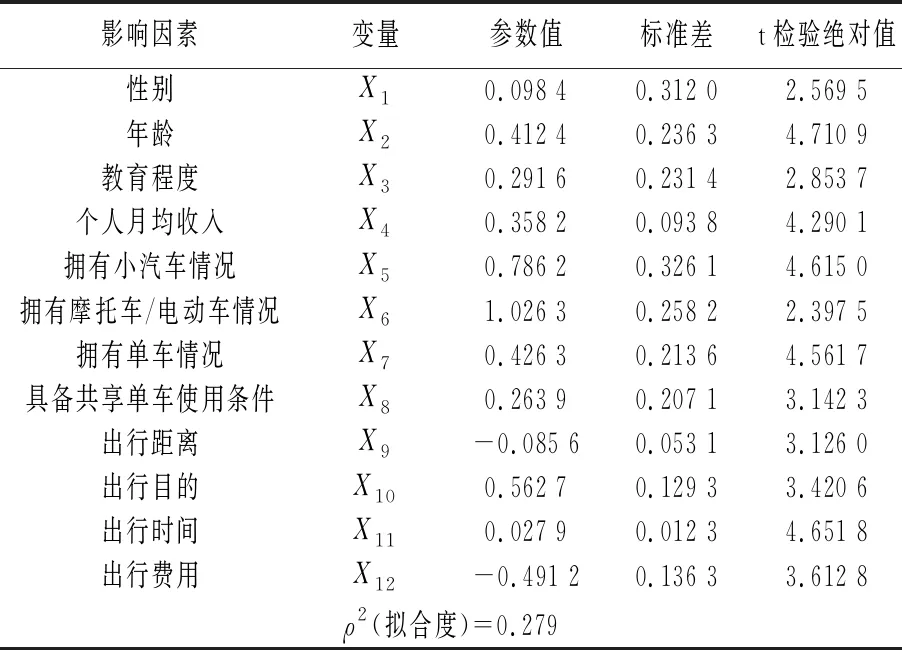
表2 参数标定结果

根据统计学检验理论，由表2可见，以上12个影响因素变量的参数t检验值的绝对值均大于1.96，表明具有95%的把握认为各影响因素变量对选择概率产生显著影响，且其符号的正负与实际情况对应。故表中12个特征变量对城市居民出行方式选择行为有显著影响。

ρ2cfadden决定系数，用来判定模型的拟合度，其值在0到1之间，愈接近1，说明模型的精度愈高。不过，实践证明：ρ2的值达到0.2～0.4之间时，即可认为精度相当高了。本文的决定系统ρ2的值为0.279，表明该模型的拟合比较理想，模型正确。

由此可知，模型标定参数正确，各出行方式影响因素变量参数见表3。表中，具备单车使用条件参数为0.263 9，表明具备单车使用条件的人口比例相对较少，但具备了单车使用条件会增加单车出行比例，同样也会增加步行出行和公交出行比例，这是换乘的影响，符合实际情况。

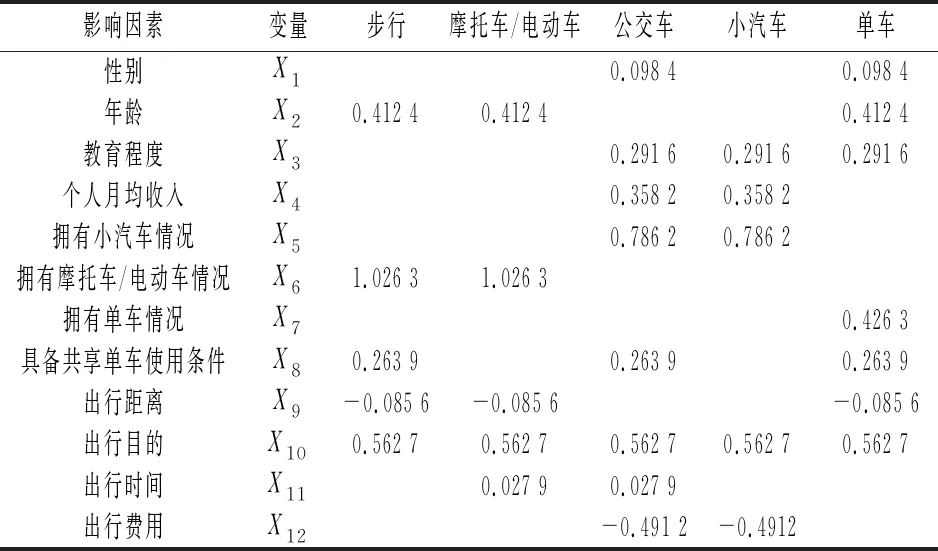
表3 出行方式参数值

2 模型实证分析

从剩余的有效调查数据中抽取181份，分析模型的正确性。根据标定参数值以及公式(2)和(3)，对应的效用函数用固定项代替，则：

V0=0.412 4X2+1.026 3X6+0.263 9X8-0.085 6X9+0.5627X10

(5)

V1=0.412 4X2+1.026 3X6-0.085 6X9+0.5627X10+0.027 9X11

(6)

V2=0.098 4X1+0.291 6X3+0.358 2X4+0.786 2X5+0.263 9X8+0.562 7X10+0.027 9X11-0.491 212

(7)

V3=0.291 6X3+0.358 2X2+0.786 2X5+0.562 7X10-0.491 2X12

(8)

V4=0.098 4X1+0.412 4X2+0.201 6X3+0.426 3X7+0.263 9X8-0.0856X9+0.562 7X10

(9)

式中，V0、V1、V2、V3、V4分别为出行方式选择步行、摩托车/电动车、公交车、小汽车、单车的出行效用。

结合效用值及公式(4)，可得5种出行方式的选择概率P0、P1、P2、P3、P4分别用式(10)、(11)、(12)、(13)、(14)计算：

(10)

(11)

(12)

(13)

(14)

其中某出行者的出行数据为：X1=1;X2=2;X3=2;X4=1;X5=1;X6=2;X7=1;X8=1;X9=1;X10=3;X11=2;X12=0。计算各出行方式的效用值和对应的概率值，见表4。由表4可见，步行出行的选择概率值最大，即该出行者根据其个人属性和出行属性选择步行出行的概率最大。

表4 出行方式选择效用值及概率值

将181份出行数据按照上述方法分别代入各出行方式效用函数公式中，进行迭代计算，求城市居民出各出行方式的概率，并对其概率求平均值，所得的结果即为模型计算结果。将模型计算结果与181份居民出行方式调研统计结果进行误差分析，结果见表5。

表5 误差结果

由表5可知，对于城市居民出行方式选择行为分析，利用模型计算的结果值与实际统计结果值差别不大，各项绝对误差值较小，最大绝对误差值仅为4.4%，可以满足实际使用要求。故模型相关因素选取较为科学合理，模型正确，具有一定的适用性。

3 结 语

本文依托湛江市居民出行数据建立了城市居民出行方式选择模型，经相关检验，模型正确、有效。因此可用于单车共享的背景下，城市居民出行方式选择的预测。

利用模型计算的结果值与实际统计结果值差别不大，各项绝对误差值较小，最大绝对误差值仅为4.4%。能准确分析模型的相关因素，具有一定的适用性。

由于城市交通中引入了共享交通工具的模式，实际交通问题较为复杂，同时在模型的研究中未考虑各因素间的相互影响、换乘等问题，故本文中利用非集计模型对单车共享下城市居民出行方式选择行为的研究有待进一步完善。