分数阶复值时滞神经网络的准一致同步
刘苑醒,张玮玮,张红梅
(安庆师范大学数理学院,安徽安庆246133)
复值神经网络的状态向量、连接权值和激活函数都是复值,它不仅是实值神经网络的简单扩展,而且其性质也更为复杂。复值神经网络可以解决一些实值神经网络无法解决的问题,比如用于异或问题和对称性问题的检测[1]。分数阶微积分是关于任意阶微分和积分的理论,也是整数阶导数和积分在任意阶上的推广。分数微分方程被认为是生物学、化学、物理、医学、经济学和其他科学领域中对实际问题进行建模的有力工具,其主要优点是分数阶系统具有遗传和无限记忆的特点。因此,许多研究者将分数算子应用到神经网络中,建立分数阶神经网络模型,并且取得了许多研究成果,比如投影同步[2]、全局Mittag-Leffler同步[3]、固定时间反同步[4]和自适应投影同步[5]。其中在文献[2]中,利用分数阶不等式、拉普拉斯变换和建立一种简单的线性控制策略来实现分数阶复值递归神经网络的投影同步;文献[5]通过在复数域上构造新的分数阶微分不等式和设计新的自适应混合控制器,利用分数阶李雅普诺夫引理和复变函数理论得到了分数阶复值神经网络自适应同步的充分条件。另一方面,研究整数阶模型的方法不能简单应用到分数阶模型中,最好用分数阶的理论来研究分数阶模型,这在技术方面为研究分数阶复值神经网络的动力学特征带来了一定的困难。应该认识到在实际同步实现中,同步误差不能总是随着时间接近零,而是波动的,这使得研究准一致同步有一定的必要性。然而在先前的文献中研究分数阶复值时滞神经网络的准一致同步较少。基于此,本文选取一种比较简单的线性控制器,利用Hölder 不等式、Cauchy-Schwartz不等式、Gronwall不等式和不等式放缩技巧分别在1 2 ≤α < 1和0 < α < 1 2的两种情况下讨论分数阶复值时滞神经网络模型的准一致同步,并得到保证分数阶系统的准一致同步的充分条件。
在本文中,Pn表示n维实数空间,Rn×m是一组n × m 阶实矩阵。上标“T”表示转置。ℂ,ℂn,ℂn×m分别表示所有复数的集合、所有n维复数向量的集合以及所有n×m阶复值矩阵的集合。i表示虚数单位,即对于任意复数z=x+iy∈X,符号表示 z 的模,即给定向量表示z的2-范数,即表示由M 到N 的n 阶连续可微函数组成的空间。对于函数ψ(t):[t0- τ,τ]→ ℂn,定义范数。
1 预备知识
定义1[6]函数h(t)的非整数α(α>0)阶的分数积分的定义其中Γ(⋅)是Gamma函数。
定义2[6]函数h(t)的α分数阶Caputo导数定义如下:
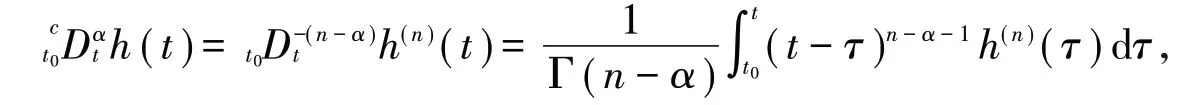
其中n-1< α < n∈ℤ+,特别地,当0 < α < 1时,有。
引理1[7]若
引理2[8](Hölder 不等式)假设q,p>1,且则
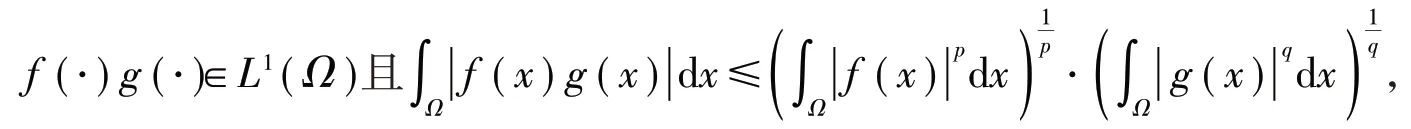
其中L1(Ω)是所有勒贝格可测函数f的Banach空间,其中f:Ω →ℝ且。
特别地,令p,q=2,就得到Cauchy-Schwartz不等式:
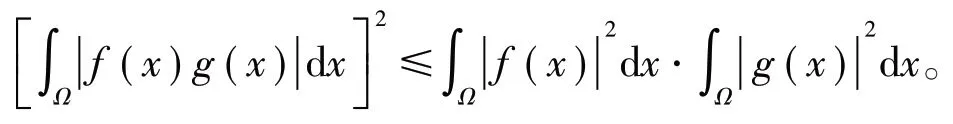
引理3[9]令n∈ℕ,ω>1,则。
引理4[10](Gronwall 不等式)若其中所涉及的所有函数在[t0,T)上连续,T ≤∞且k(t)≥0,则x(t)满足。
在本文中,考虑以下分数阶时滞复值神经网络:
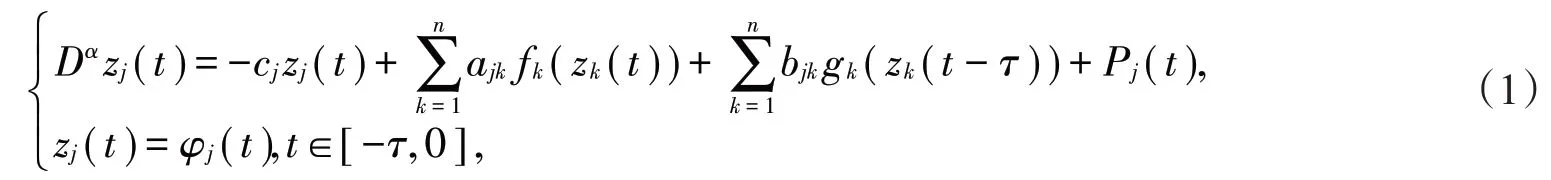
其中j=1,2,…,n,其向量形式为

其 中 0 < α < 1,n 是 神 经 元 的 数 量 ,z(t)=(z1(t),z2(t),…,zn(t))∈ℂℂn是 状 态 向 量 ,F(z(t))=(f1(z1(t)),f2(z2(t)),…,fn(zn(t)))Τ、G(z(t))=(g1(z1(t)),g2(z2(t)),…,gn(zn(t)))Τ分别表示无时滞和有时滞的神经元有界激活函数,A=(ajk)n×n、B=(bjk)n×n∈ℂℂn×n分别表示无时滞和有时滞的连接权重矩阵,C=diag{ c1,c2,…,cn}∈ℝn×n(cj>0)是自反馈连接权重矩阵,P(t)=(P1(t),P2(t),…,Pn(t))T∈ℂn是外部输入向量,τ是时滞且τ>0,模型(2)定义为驱动模型。
为了讨论分数阶复值时滞神经网络的准一致同步,定义响应系统如下:
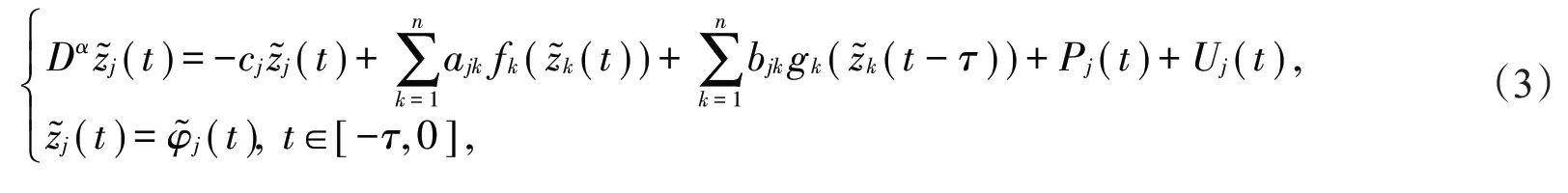
其向量形式:
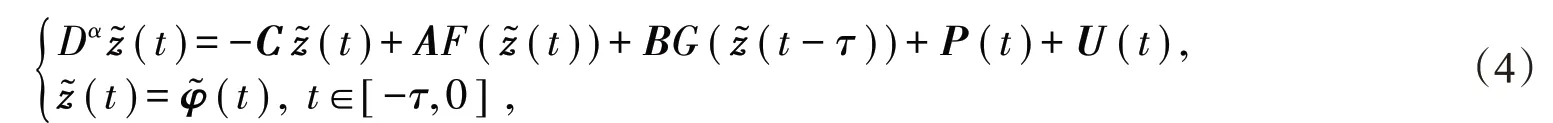
其中U(t)为控制器且U(t)=(U1(t),U2(t),…,Un(t) )Τ。
假设1令z=x+iy,F(z(t))和G(z(t-τ))是解析的,把它们用实部和虚部分开来表示:
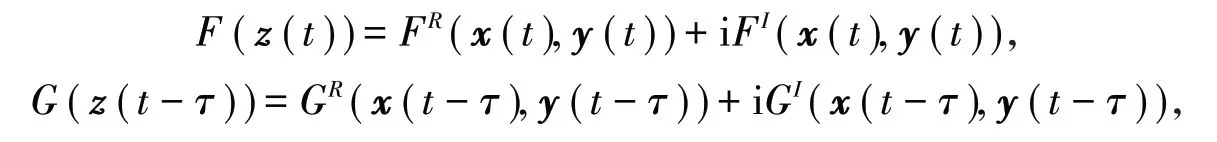
同样地,复数矩阵 A 和 B 也可以表示为 A=AR+iAI,B=BR+iBI,令,外部输入向量P(t)表示为P(t)=PR(t)+iPI(t),控制器U(t)表示为U(t)=UR(t)+iUI(t)。
假 设 2在 ℝ2上 满 足 Lipschitz 条 件 ,即 对 任 意存在正数使得
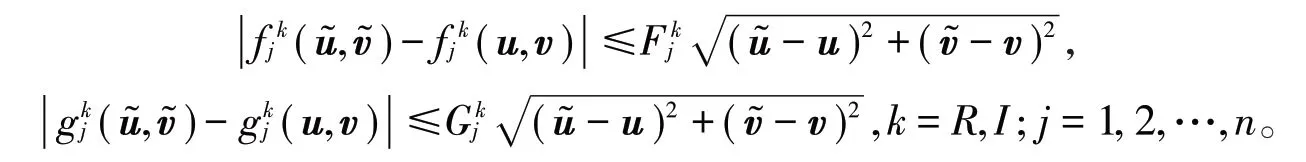
备注1注意到对于任意有:


同样地,也可以得到:
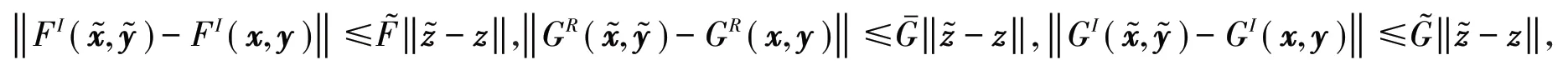
将分数阶复值神经网络模型(2)和(4)中的状态向量、连接权重矩阵、向量激活函数、外部输入向量和控制器分成实部和虚部来表示得到:
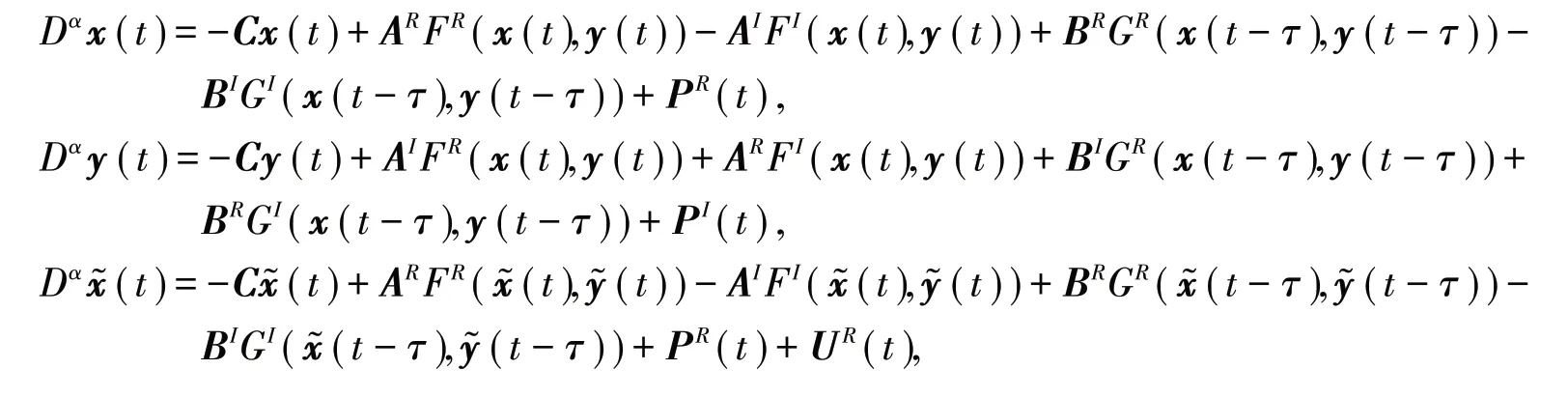
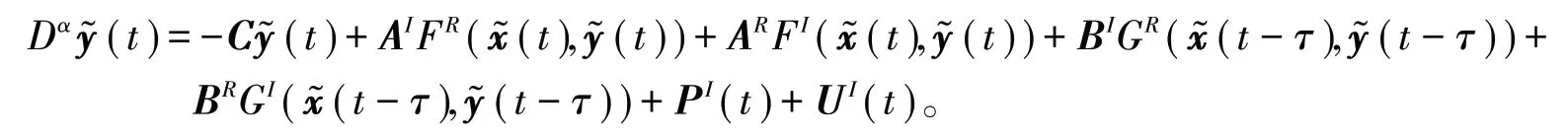
定义驱动系统与响应系统之间的误差为e(t),令
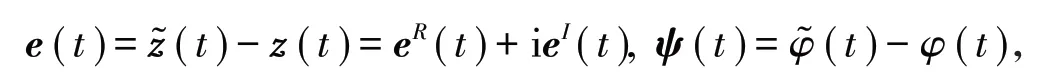
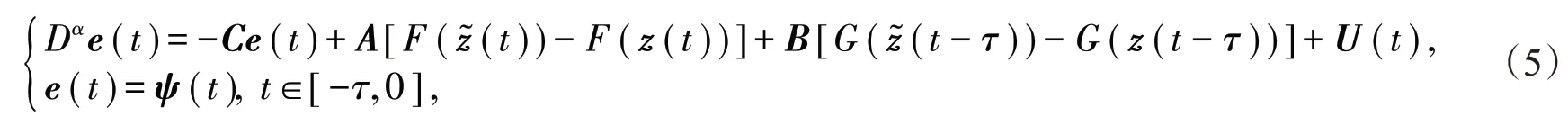
选取响应系统(4)中的控制器:

其中H =diag{h1,h2,…,hn}∈ℝn×n,则误差系统(5)可改写为
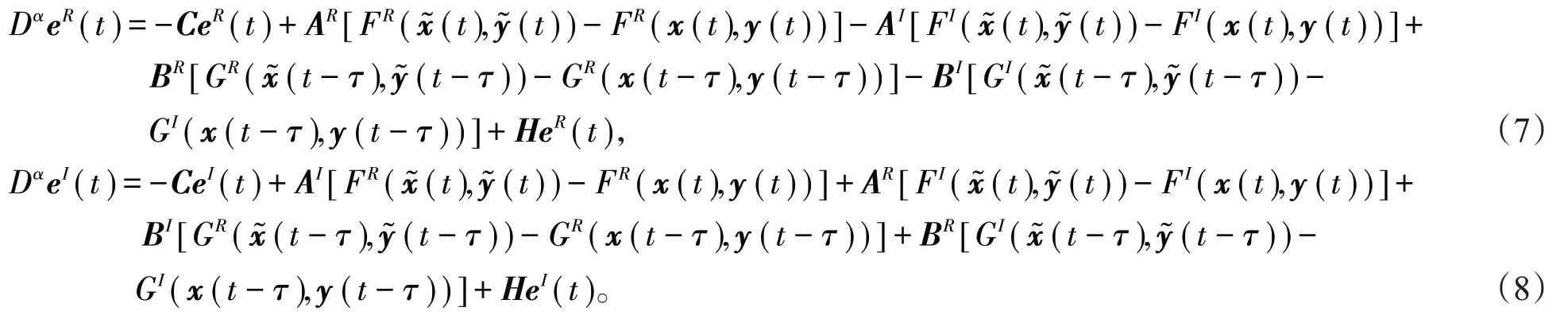
定义 3[11]对于误差系统(5),若对于∀ε>0,存在两个常数0 < δ < ε,Τ>0,当‖ ‖e(t0) < δ 时,有对∀t∈J=[t0,t0+Τ],其中t0为初始观测时间,则称分数阶神经网络的驱动系统(2)和响应系统(4)实现准一致同步。
根据引理1,系统(7),(8)可以分别表示为
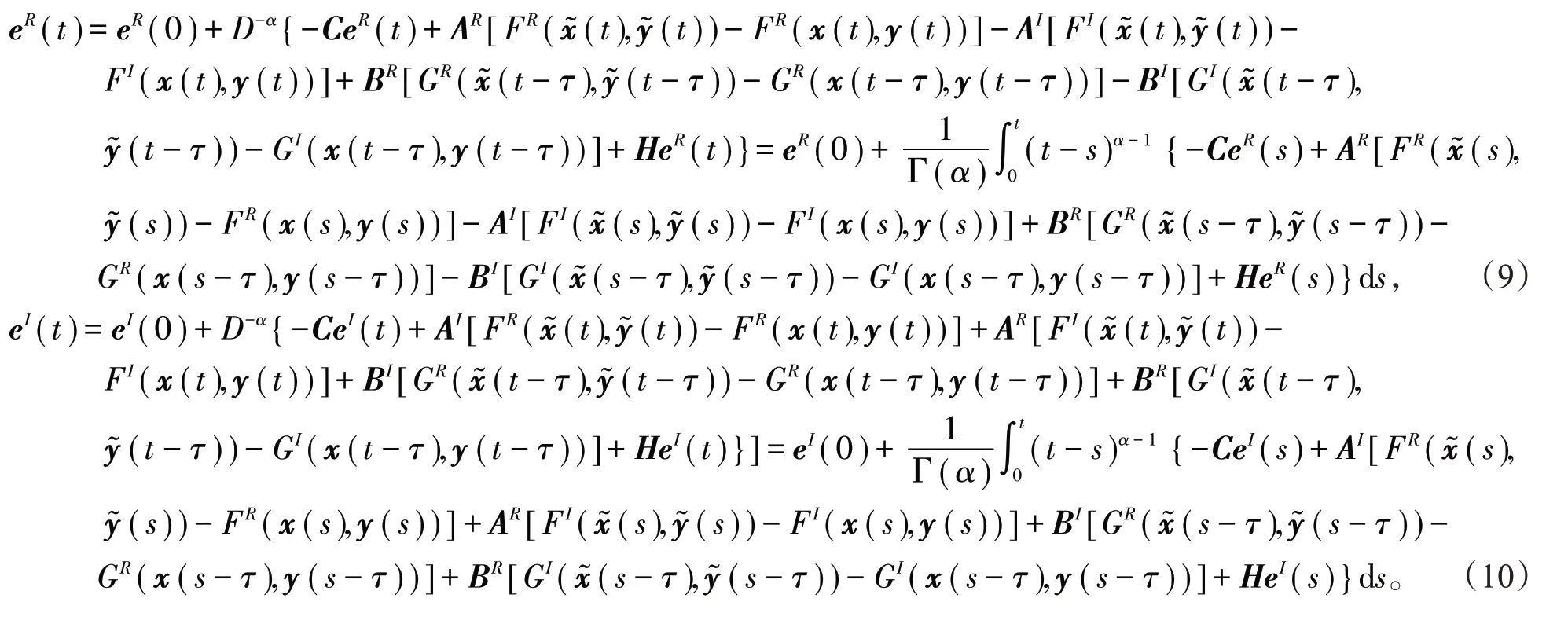
2 主要结果
定理1在假设1和假设2的前提下,若1 2 ≤α <1且
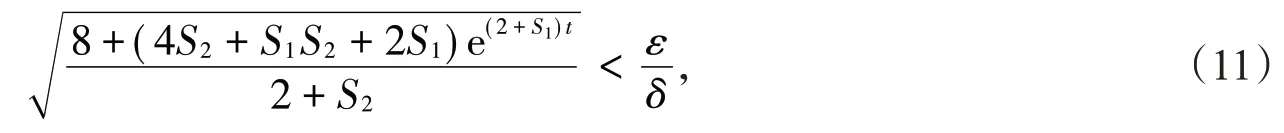
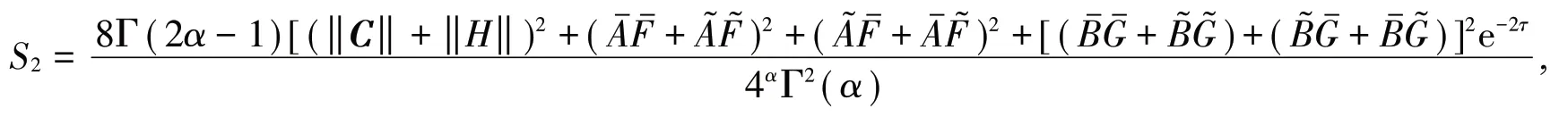
则对于t∈J=[0,T],分数阶神经网络的驱动系统(2)和响应系统(4)实现准一致同步。
证明由假设1和假设2得到
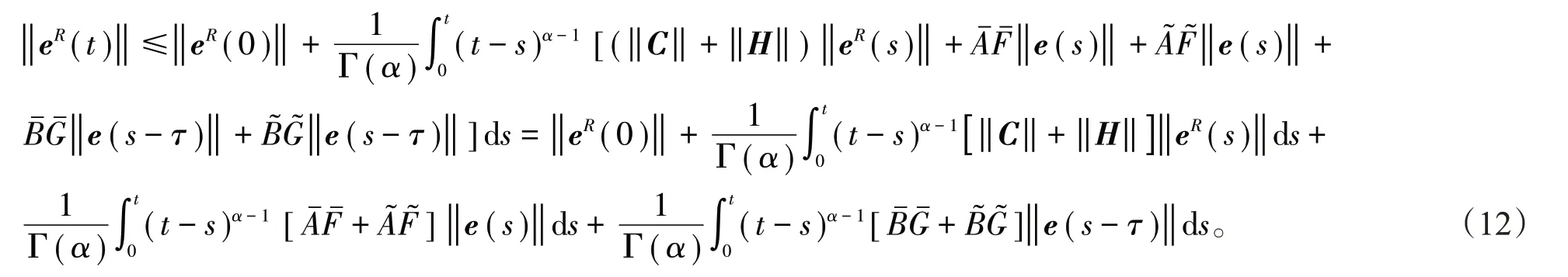
利用引理2,得到
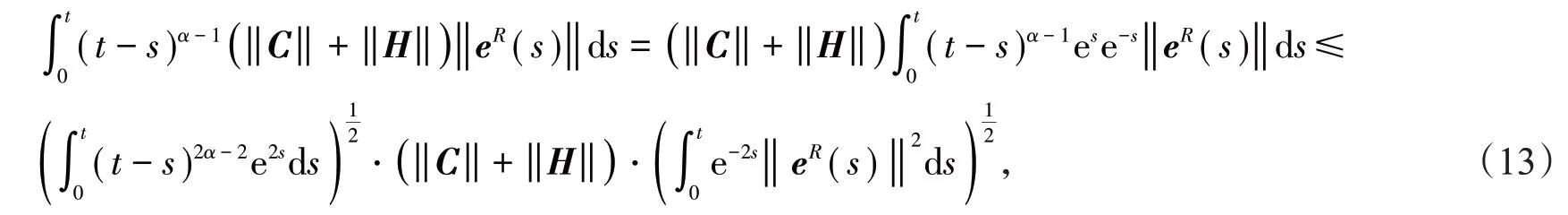
同样地,可以得到

将(13)~(16)式代入(12)式得到
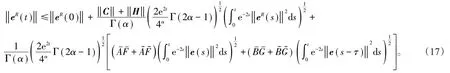
利用引理3,令n=4,ω=2,从(17)式中得到
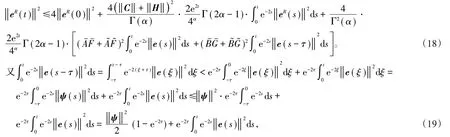
将(19)式代入到(18)式得到
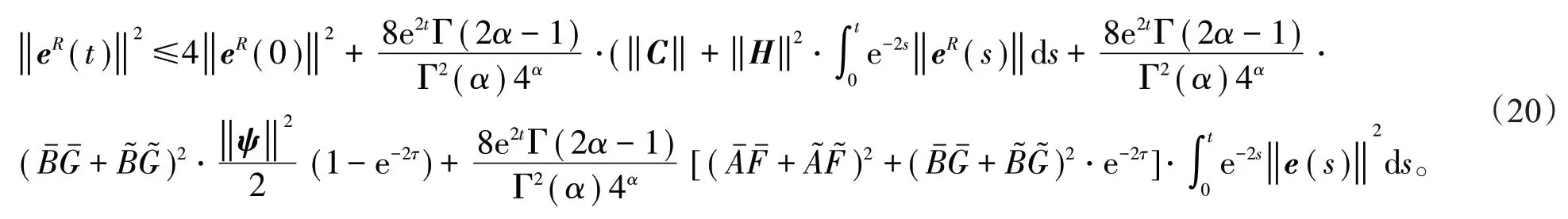
同理,可以得到
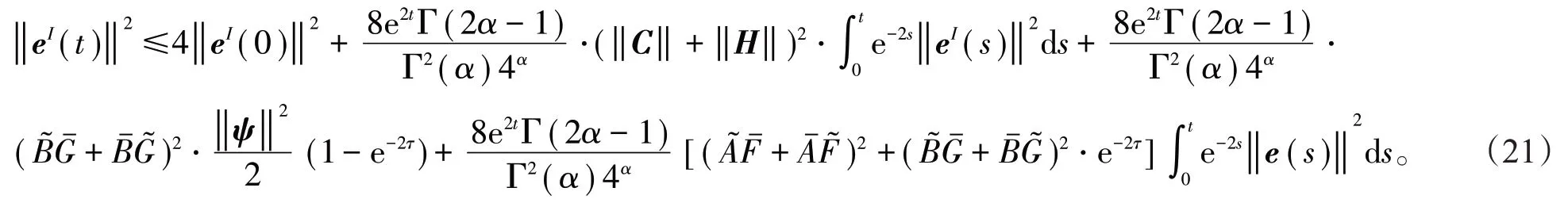
通过(20),(21)式可以得到
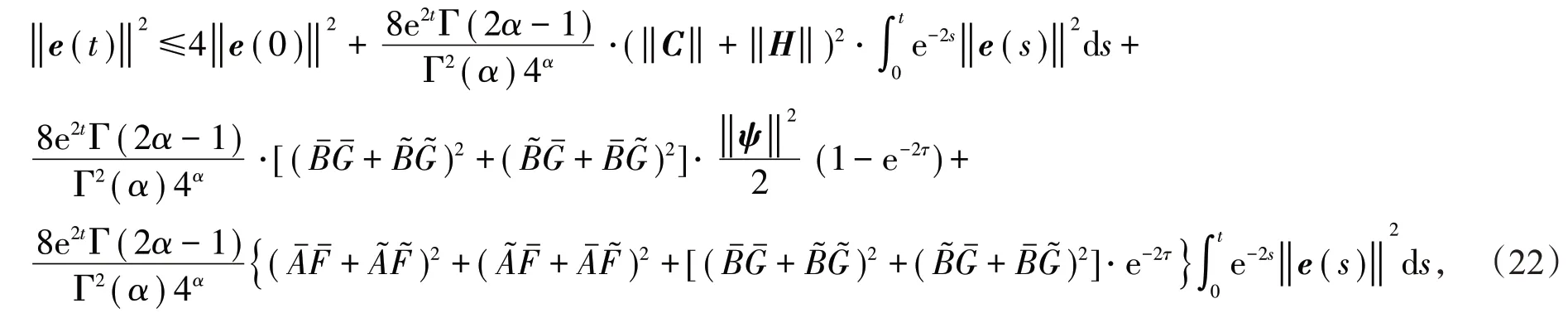
在(22)式左右两端同时乘以e-2t得到
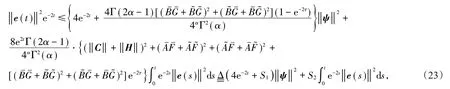
其中S1,S2是如定理1中的形式,通过Gronwall不等式得到
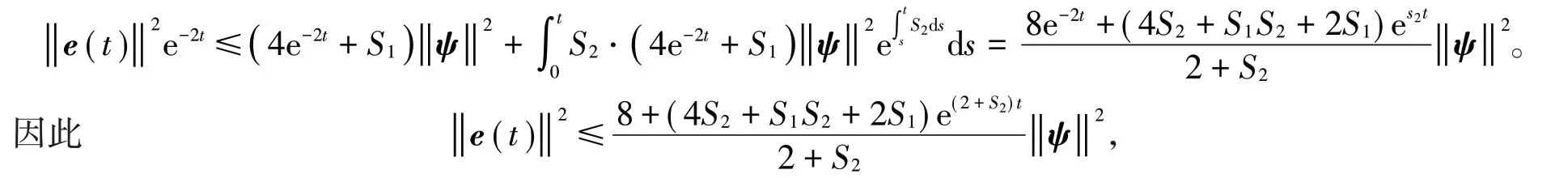
定理2在假设1和假设2的前提下,若0 ≤α <1 2且
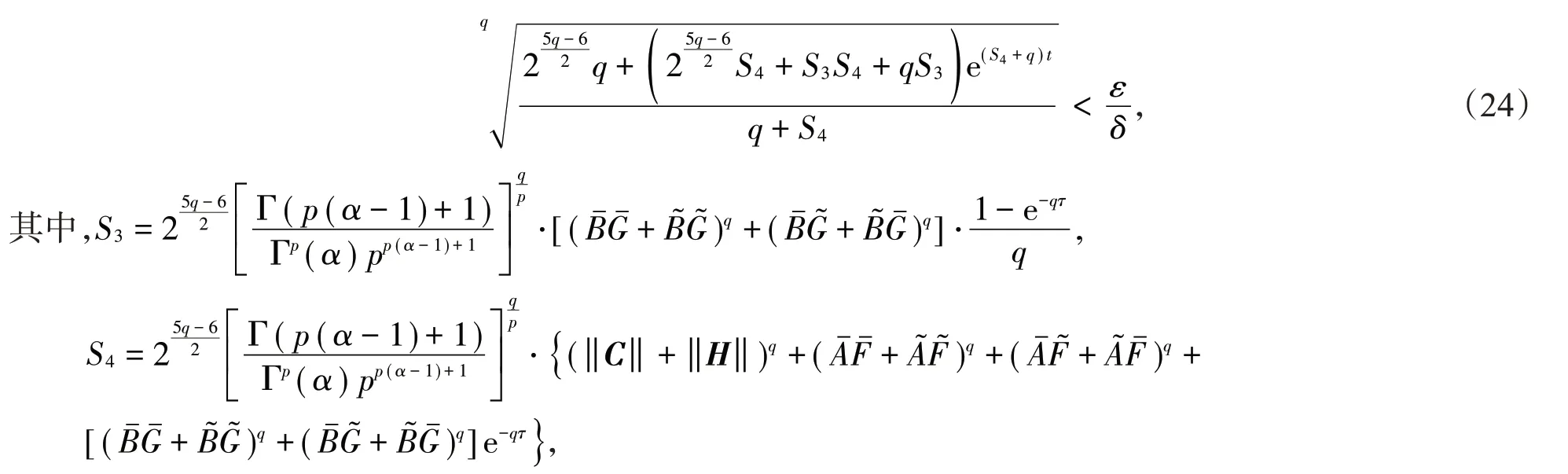
p=1+α,q=1+ 1 α,则对t∈J=[0,T],分数阶神经网络的驱动系统(2)和响应系统(4)实现准一致同步。
证明与定理1相同,有:
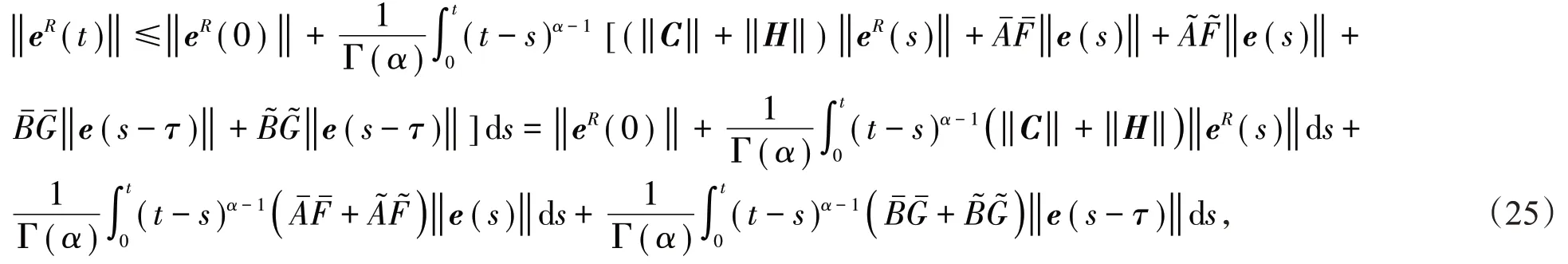
利用引理2得到
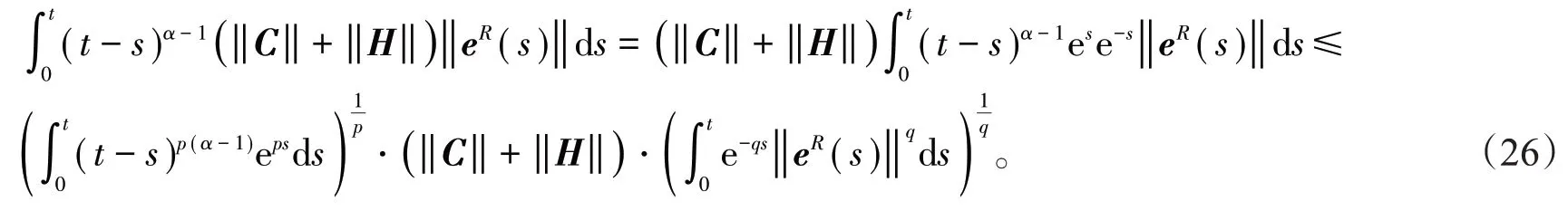
同样地,可以得到
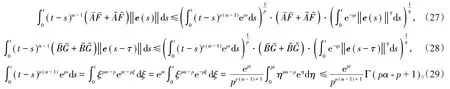
将(26)~(29)式代入(25)式得到
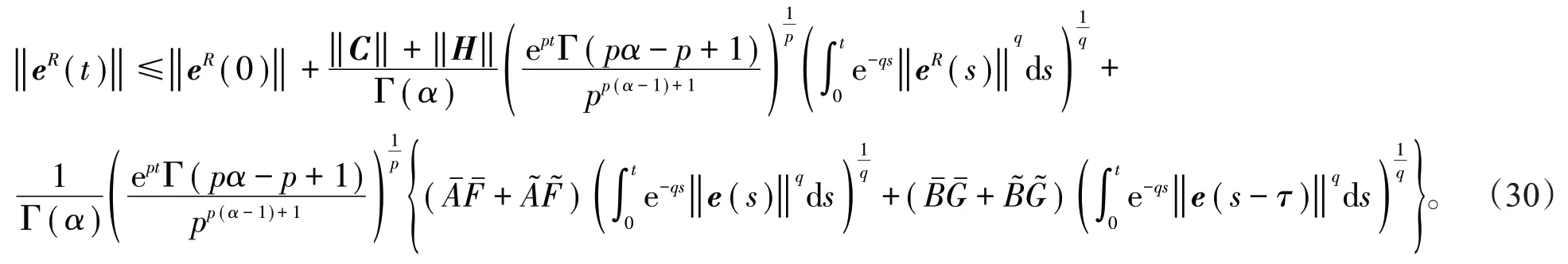
利用引理3,令n=4,ω =q,从(30)式得到
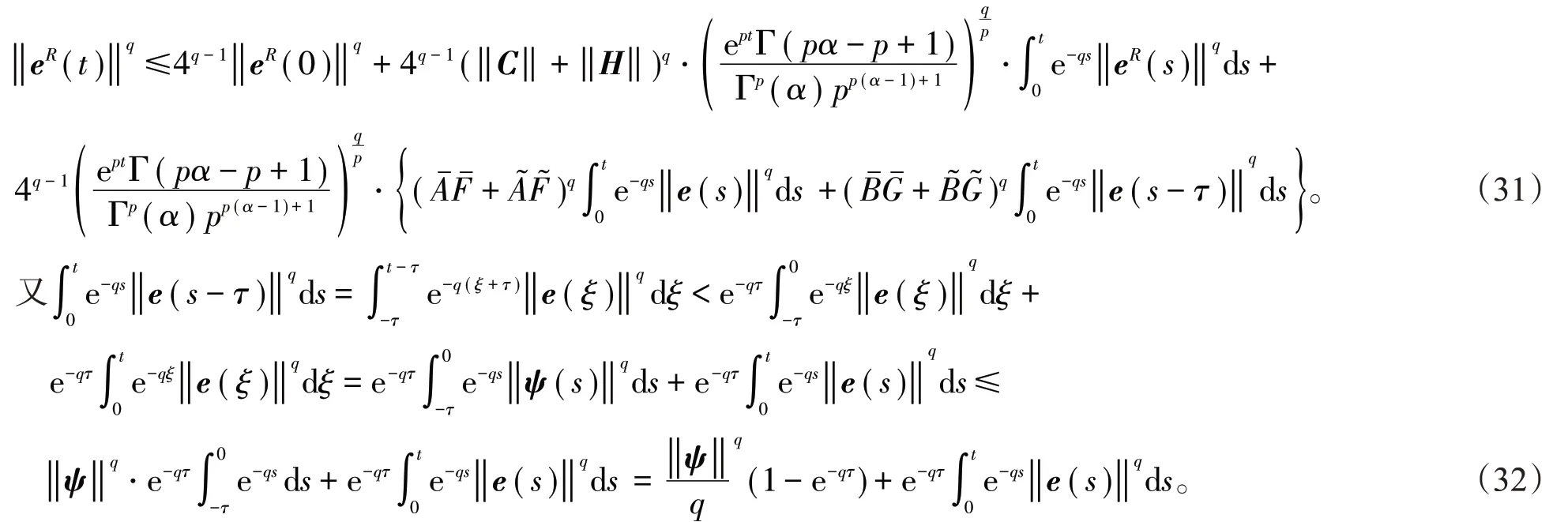
将(32)式代入到(31)式得到
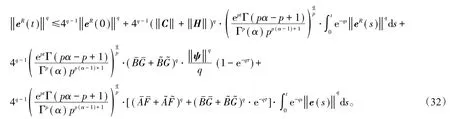
同理,可以得到
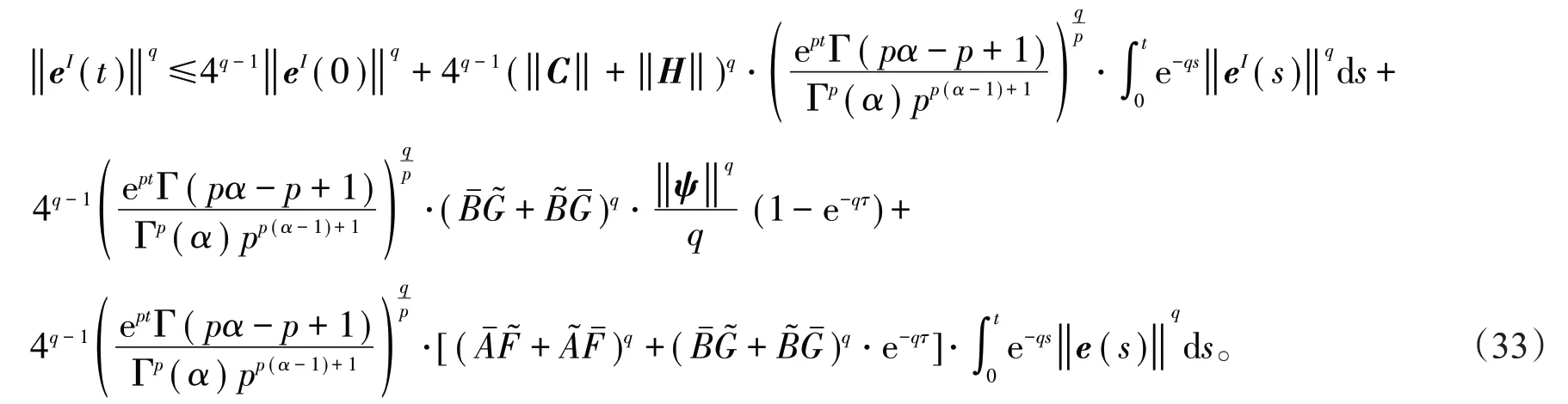
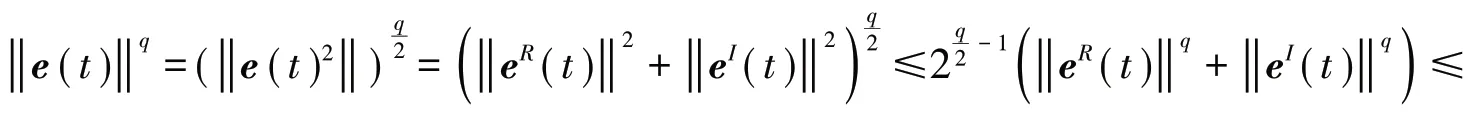
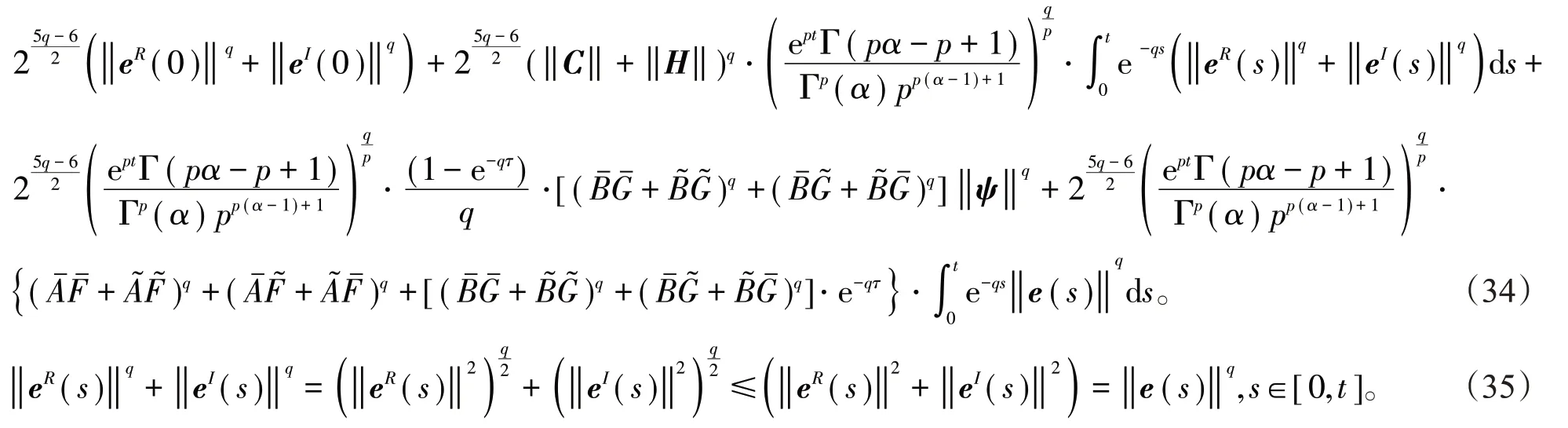
把(35)式代入到(34)式后,并在(34)式左右两边同乘以e-qt得到
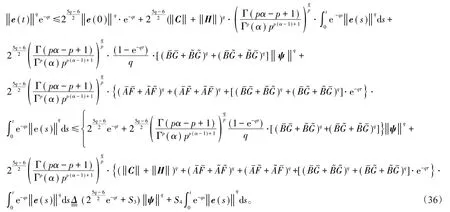
其中S3,S4如定理2中的形式,通过Gronwall不等式得到
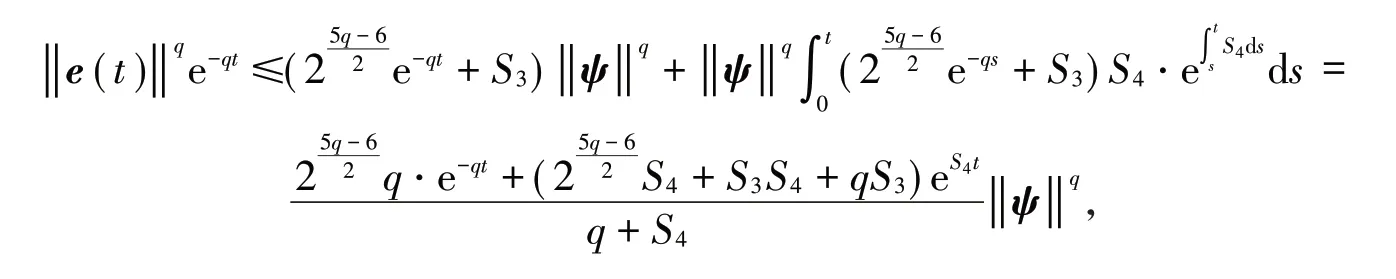
因此
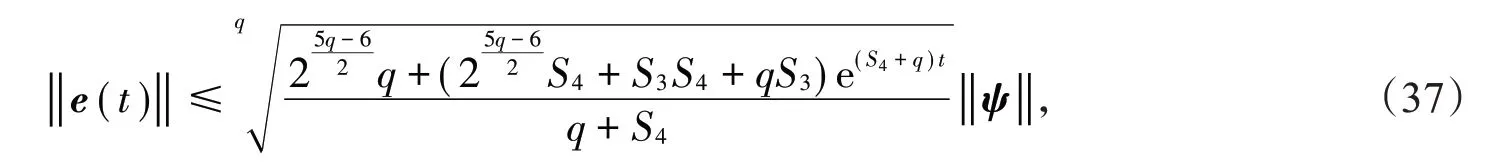
3 应用举例
为了验证所得结果的正确性以及可行性,现给出数值模拟结果如下。
例1 考虑一个具有双神经元的分数阶复值神经网络作为驱动系统:
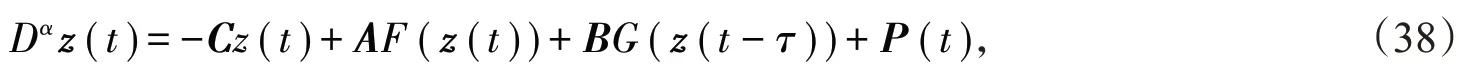
其中
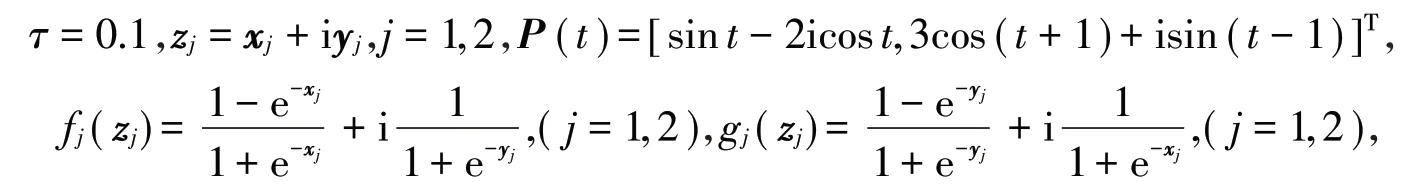
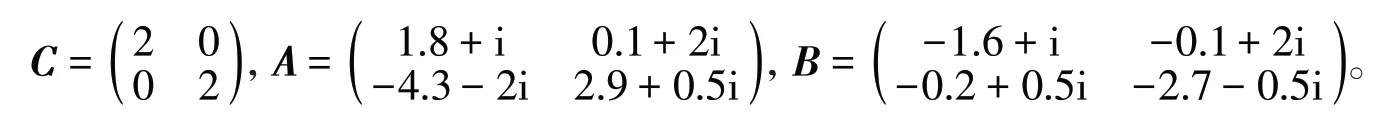
分数阶复值神经网络的响应系统为:
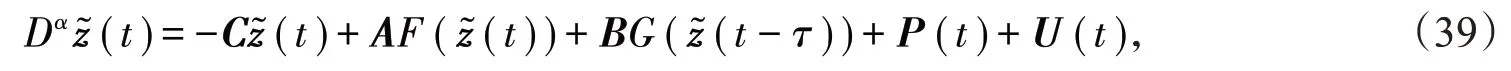
(1)当α=0.88 时,取控制器中的H为取α=0.88,τ=0.1,δ=0.1,ε=1,由定理1可以得到S1≈0.616 9,S2≈23760。将上述值代入(11)式,因分数阶神经网络的驱动系统(2)和响应系统(4)实现准一致同步的时间Te≈1.5819,得不等式(11)成立。取初始条件为对于s∈[-1,0],得到图1~图4。
(2)当α=0.49 时,取控制器中的矩阵δ=0.1,ε=1,由定理2 可以算出S3≈0.099 5,S4≈115 108.6。因分数阶神经网络的驱动系统(2)和响应系统(4)实现准一致同步的时间Te≈2.006 0,将上述值代入(24)式,得取系统中的初始条件为z1(s)=500-300i,z2(s)=150-100i,z˜1(s)=-250+100i,z˜2(s)=-75+75i,对于s∈[-1,0],得到图5~图8。
4 总 结
本文讨论了在1 2 ≤α<1和0 <α<1 2两种情况下,分数阶复值时滞神经网络的准一致同步问题。通过利用Hölder不等式、Cauchy-Schwartz不等式、Gronwall不等式和一些不等式技巧,实现了驱动-响应系统的准一致同步,并利用数值模拟说明所得结果是正确和可行的。应该指出的是,许多复杂的系统近年来得到了广泛的研究,而本文选择的控制器比较特殊。将来会利用一些新的技术来研究更复杂系统的一些同步问题,譬如有限同步、定时同步等等。
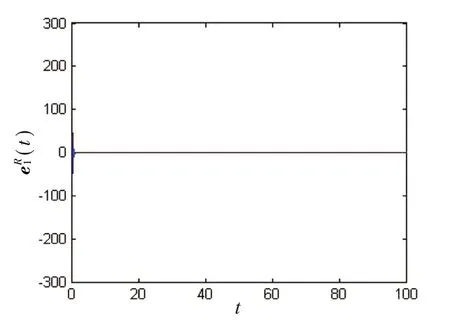
图1 误差(t)的状态轨迹
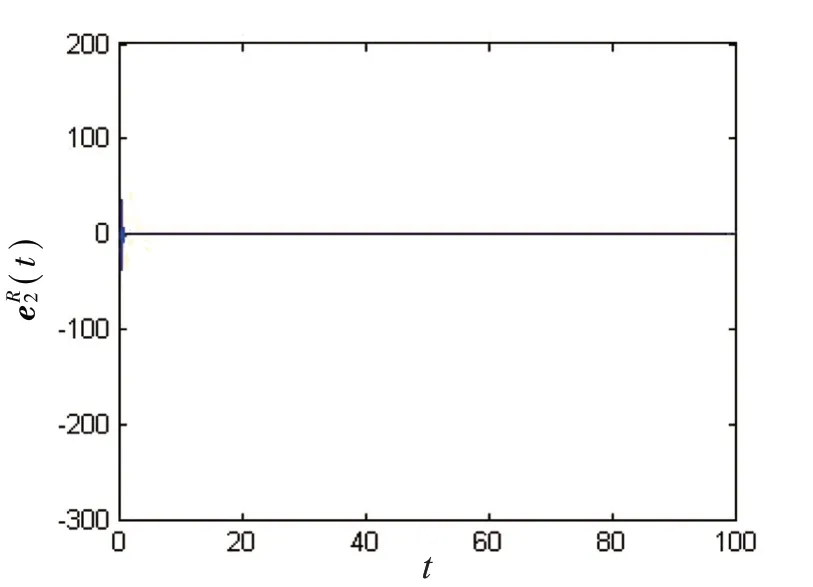
图2 误差(t)的状态轨迹
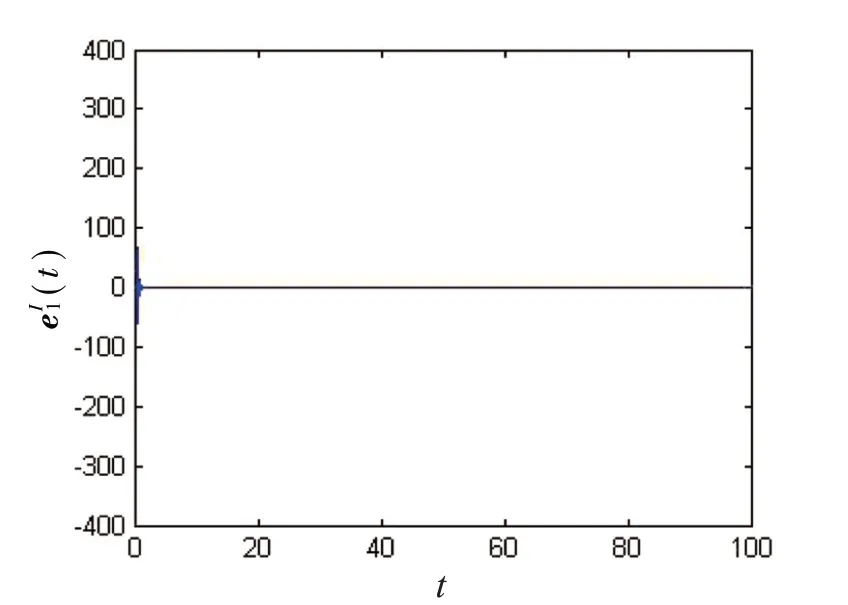
图3 误差(t)的状态轨迹

图4 误差(t)的状态轨迹

图5 误差(t)的状态轨迹
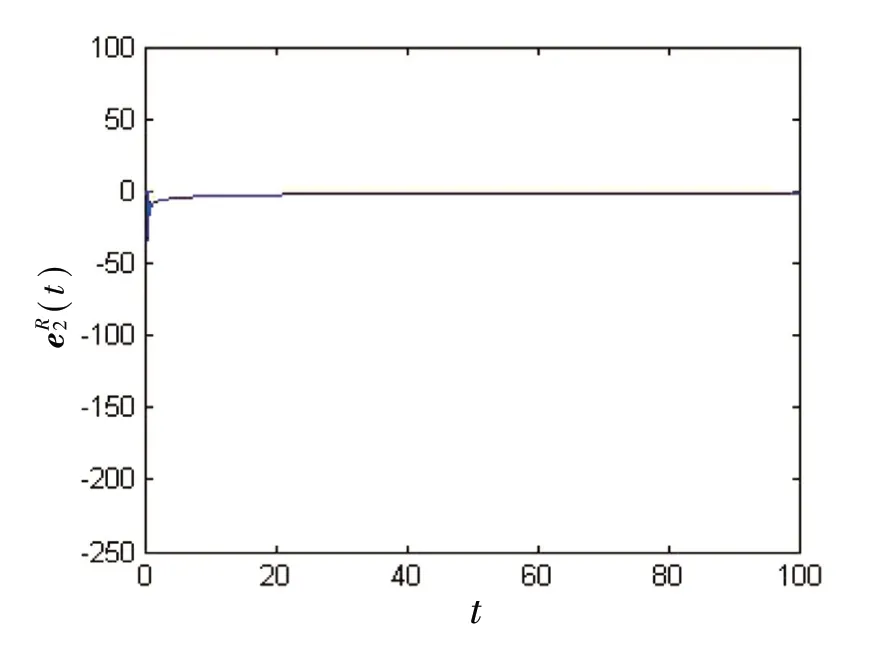
图6 误差(t)的状态轨迹
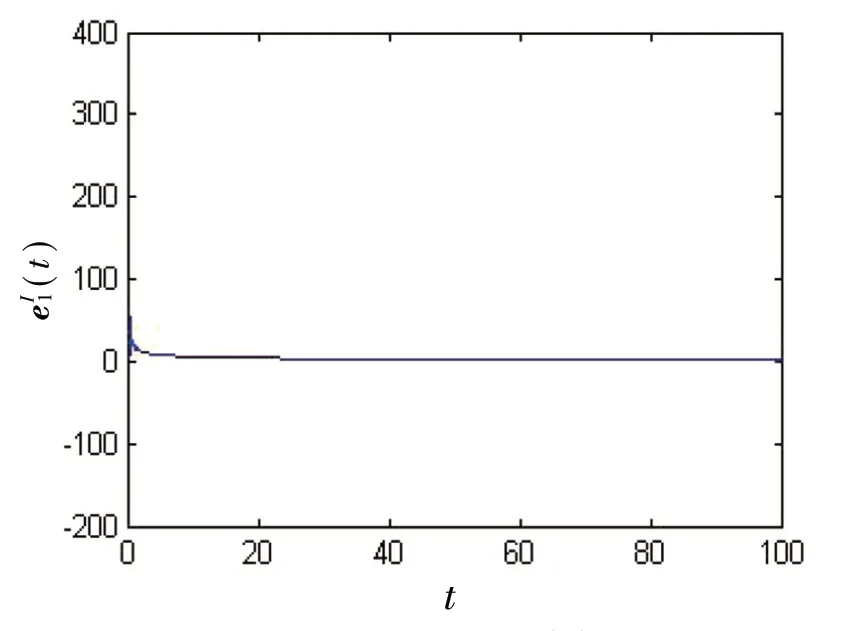
图7 误差(t)的状态轨迹
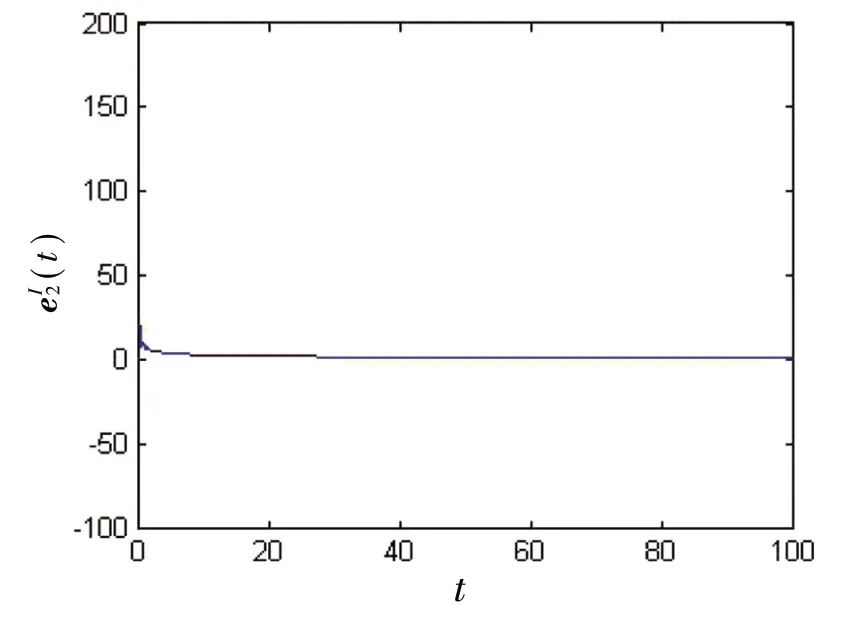
图8 误差(t)的状态轨迹

