基于ISOMAP与Adaptive-Lasso的日平均气温预测模型
许 欢,朱华亮,温华洋
(1.合肥幼儿师范高等专科学校基础部,安徽合肥230013;2.安徽省气象信息中心,安徽合肥230031)
近年来,全球气候呈现快速性、灾难性等特点,强风、气温升高和强降雨等极端天气频发,严重影响了人们的日常生活、社会生产、军事活动等。开展气候变化研究,预测未来的气象变化,对极端天气进行提前预防和抵御,以减少恶劣气象所造成的不必要的损失,变得尤为重要[1]。国内外学者针对气象预测已经做了大量的研究应用,如文献[2-3]分别基于贝叶斯理论和自然灾害风险理论,对短期风速和降雨进行了预测;文献[4-5]利用神经网络和极限学习机,基于气象预报数据建立了气象预测模型。然而从研究中可以发现,大多数文献都是对单一气象因素的分析,对多元气象因素的研究却相对较少。
随着信息时代的到来,使得海量的气象数据信息获取成为可能。然而,海量的气象数据信息种类和数量也给问题分析过程带来了巨大挑战,数据降维是解决这类问题的有效工具,因此被广泛使用。主成分分析(PCA)方法是人们提取气象数据特征常用的方法,其对于本身具有线性结构的数据集的特征提取是非常有效的,而对于具有非线性结构的气象数据的效果却并不理想[6]。流形学习中的等距特征映射(ISOMAP)方法具有非线性降维能力,此外,Lasso方法可以很好地对模型参数进行压缩,使得某些回归系数变小甚至为0,从而进一步优化模型[7]。Zou[8]提出的Adaptive-Lasso方法对不同系数使用不同程度的压缩效果,使Lasso估计具有Oracle性质。本文针对合肥2017.1.1—2018.8.31气象数据信息,在对气象因素使用ISOMAP方法降维的基础上运用Adaptive-Lasso方法进行建模,预测日平均气温。将结果与基于ISOMAP及Adaptive-Lasso的模型预测结果相比较,发现通过ISOMAP与Adaptive-Lasso方法建立的回归模型能更好对日平均气温进行回归预测。
1 ISOMAP方法
ISOMAP 方法是Tenenbaum[9]于2000 年提出的以线性简约多维尺度变换方法为基础,以保持观测空间样本点原有的几何结构为原则的算法[10]。在ISOMAP中,用两点间的测地距离代替直线距离,从而可以更好地表示同一流形中两点的真实距离。算法步骤如下:
(1)设样本集{a1,a2,…,an},计算任意两点ai,aj的欧氏距离de(ai,aj),利用KNN(k-NearestNeighbor)方法构造k邻域图G。
(2)用Dijkstra 算法或Floyd 算法度量任意两点ai,aj的最短路径长度作为两点的测地线距离dG(ai,aj),若aj是ai的k近邻,则dG(ai,aj)=de(ai,aj);若aj不是ai的k近邻,且{a1i,a2i,…,aki}是ai的k近邻点集,则
(3)以dG(ai,aj)作为距离矩阵D的元素,以矩阵D作为多维标度分析(MDS)的输入,得到输出。
MDS可以看作是一个特征分解过程,它的输入通常是一个距离矩阵D,D经降维后不会改变。
2 Adaptive-Lasso方法
Lasso是一种同时选择和估计变量的方法,其参数估计为
其中,X=(X1,X2,…,Xk)是预测变量矩阵,Xj=(x1j,x2j,…,xmj)Τ,j=1,2,…,k为预测变量,Y=(y1,y2,…,ym)Τ是响应变量,λ为非负正则化参数,β=(β1,β2,…,βk)Τ为回归系数。
Lasso 方法的核心在“l1惩罚”,即(1)式的第二部分。在Lasso 方法中,随着正则化参数λ的不断增大,回归系数逐渐趋向于0。当λ足够大时,此时回归系数缩小到0。
Adaptive-Lasso方法是Zou[8]于2006年在Lasso的基础上进行改进并提出的,该方法对不同系数采用不同程度的压缩,从而能够更快更好地选择出最优的特征。其参数估计为


3 实证分析
本文数据来源于安徽省气象信息中心,对合肥2017.1.1—2018.8.31日平均气温及其影响因素进行研究并建立回归预测模型。数据如下页表1所示。

表1 2017.1.1—2018.8.31合肥日平均气温及其影响因素
因因素太多,表1中不能全部列举,故省略一些因素。省略的有:日平均风速(24小时)(m/s)、日降水量(mm)、日平均地面温度(℃)。在下列进行的所有实验中,以上述600组数据中的前365 组数据进行分析,对后235组数据进行预测比较。
3.1 ISOMAP回归
对气象数据中的平均气压、平均水气压等相关因素进行ISOMAP降维,选取k=5,残差如图1所示。从图1中可以看出,当维度d≥4时,投影到低维上的残差值最小并收敛到一个定值。因此选择4为低维空间的维度,原始因素分量的相关系数如表2所示。

图1 气象数据残差曲线图
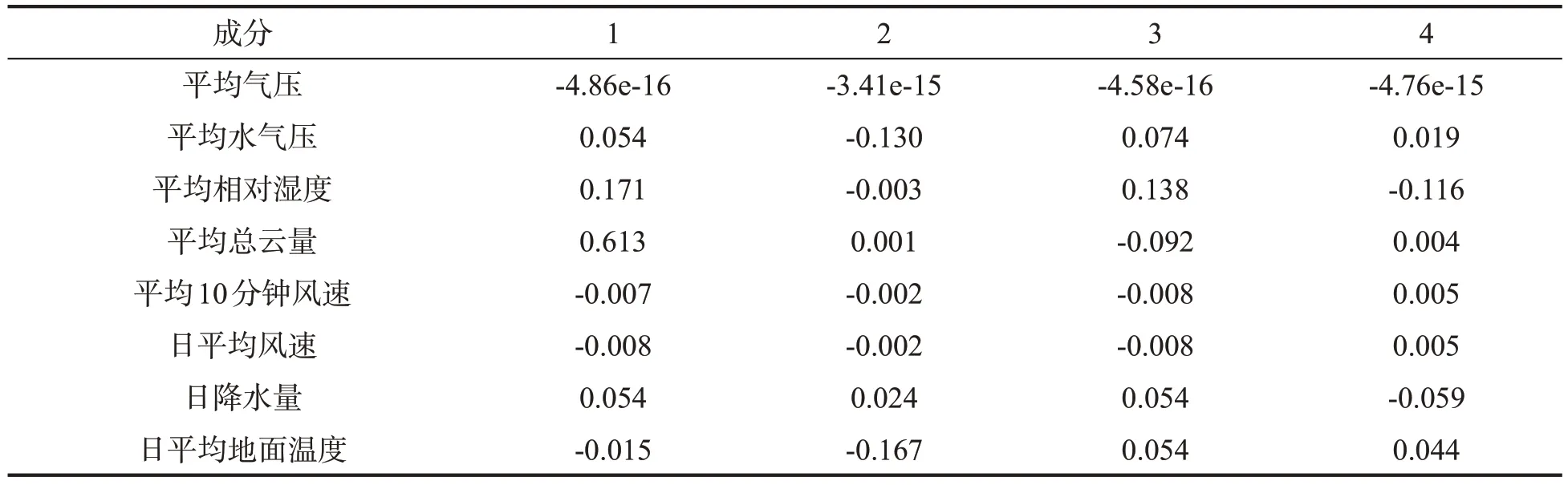
表2 原始坐标分量的相关系数
利用ISOMAP所得的成分矩阵,采用逐步回归法建立日平均气温与主成分之间的回归模型,结果如表3 所示。由此得出回归模型:y=0.016+0.035Comp1+0.577Comp2+0.345Comp3+0.095Comp4,回归模型的拟合度为0.963 2,对后235组数据根据以上模型进行预测,并将预测数据与实际数据进行比较,如图2所示,黑色代表实际值,红色代表预测值。计算其均方误差根(RMSE)为0.024。从图2可以看出,预测值与实际值走势大致吻合,在25~40和210~230这两段预测的误差较大。
3.2 Adaptive-Lasso回归
采用Adaptive-Lasso方法建立日平均气温与相关气象因素之间的回归模型,表4为各相关因素的回归系数。
基于Adaptive-Lasso方法的回归模型:y=0.002+0.306X2-0.034X3+0.008 5X4+0.621X8,模型拟合度为0.965 3,与上节相同,对后235组数据根据以上模型进行预测,图3为预测数据与实际数据的比较。计算其均方误差根为0.021。从图3可以看出,预测值与实际值走势大致吻合,在25~40这段预测的误差较大。

表3 日平均气温与主成分间的回归模型

表4 相关因素的回归系数

图2 ISOMAP方法预测值与实际值的比较

图3 Adaptive-Lasso方法预测值与实际值的比较
3.3 基于ISOMAP的Adaptive-Lasso回归模型
应用ISOMAP方法对气象因素进行降维,再采用Adaptive-Lasso方法建立日平均气温与主成分之间的回归模型,结果如表5 所示,得到回归模型:y=0.015+0.041Comp1+0.602Comp2+0.265Comp3,模型拟合度为0.970 1。对后235组数据根据以上模型进行预测,预测数据与实际数据的比较如图4所示。
从图4中可以看出,预测值与实际值基本吻合,预测的均方误差根为0.019,拟合效果较好。与基于ISOMAP 与Adaptive-Lasso 建立的模型相比,基于ISOMAP 的Adaptive-Lasso 方法建立的回归模型能更好地拟合日平均气温与其他相关气象因素之间的关系。

表5 回归系数

图4 ISOMAP-Adaptive-Lasso方法预测值与实际值的比较
4 总 结
本文针对合肥2017.1.1—2018.8.31 日平均气温及其影响因素,分别建立了基于ISOMAP 逐步回归模型、Adaptive-Lasso回归模型和基于ISOMAP的Adaptive-Lasso回归模型。结果表明,基于ISOMAP的Adaptive-Lasso方法建立的回归模型能够很好地对日平均气温进行回归预测。

