具有时滞状态导数反馈的一阶多智能体系统的收敛速度分析

晋守博

（宿州学院数学与统计学院，安徽宿州234000）

多智能体系统是一种特殊的分布式系统，被广泛应用于飞行器编队控制、机器人编队控制和集群控制等方面，对于复杂问题具有较强的处理能力。目前，一致性控制是多智能体系统研究的核心问题，许多学者都在关注如何提高多智能体系统实现一致性的收敛速度，研究表明，影响收敛速度的主要因素包括通信拓扑结构、通讯协议和协议权值等[1-5]。Olfati-Saber等证明了多智能体系统实现一致性的收敛速度正比于拉普拉斯矩阵的第二最小特征值，指出了代数连通度是提高收敛速度的决定因素[6]。随后，Olfati-Saber发现在小世界网络中，通过几个智能体经过不多的步数就与相邻智能体连接的方法，实现一致性的收敛速度会更快[7]。Xiao等证明了改变拓扑结构的权重可以提高收敛速度，并给出了收敛速度最大时对应的最优权重[8]。Kim等提出利用最佳顶点配置的方法增大拓扑结构的代数连通性，从而加快收敛速度[9]。Jin 等证明了不改变权重，只改变信息传递方式同样能够提高收敛速度[10]。上述文献主要是从拓扑结构、通讯协议和协议权值方面研究如何提高实现一致收敛的速度，本文将给出一种具有加权项的时滞状态导数反馈一致性协议，研究多智能体系统实现一致收敛的速度，在一定程度上完善了文献[11]的方法。本文主要研究下面一阶多智能体系系统

这里xi(t)∈ℝ表示智能体i的状态，ui(t)代表智能体i的输入变量。

对于具有时滞的多智能体系统，Olfati-Saber等提出了线性一致性协议[6]

并证明了在无向连通网络下，系统实现渐近平均一致的充要条件是通讯时滞τ＜π 2λN，这里λN对应拉普拉斯矩阵的最大特征值，文献[11]用xi(t-τ+β)替换协议（2）中的xi(t-τ)，并通过近似计算提出了一类具有时滞状态导数反馈的线性一致性协议，证明了对于无向连通网络拓扑，在不改变拓扑结构的条件下，通过调节反馈强度，能够同时提高系统的时滞鲁棒性和实现一致性的收敛速度，但是他们采用的方法对于较大的反馈强度存在误差偏大的问题。为了降低误差，本文令xi(t-τ+β)≈v1xi(t-τ)+v2βx˙i(t-τ)，提出如下具有加权项的时滞状态导数反馈的一致性协议

其中反馈强度β满足0 ＜β＜τ，权重常数v1＞v2＞0。

定 义 1[11]将通讯时滞τ∈(0,τmax)分割为(0,τ1],(τ1,τ2),[τ3,τ4],…,[τk-1,τk],(τk,τmax)，当τ∈(τ1,τ2)⋃(τ3,τ4)⋃…⋃(τk,τmax)时，多智能体系统（1）称为超临界时滞多智能体系统；当τ∈(0,τ1]⋃[τ2,τ3]⋃…⋃[τk-1,τk]时，多智能体系统（1）成为亚临界时滞多智能体系统。

多智能体系统（1）在一致性协议（3）下的闭环形式为

下面讨论具有加权项的时滞状态导数反馈的一致性协议对实现一致性收敛速度的影响。

1 主要结论

为了分析具有加权项的时滞状态导数反馈对多智能体系统实现一致性的收敛速度的影响，需要讨论反馈强度对闭环形式（4）极点的影响，记x(t)=[x1(t),x2(t),…,xN(t)]，将闭环系统转化为如下紧凑形

这里L是相应的拉普拉斯矩阵。

定理1当多智能体系统（1）为超临界时滞多智能体系统时，存在正常数β*，使得当时滞状态导数反馈强度β∈(0,min{τ,β*})时，多智能体系统（1）在一致协议（3）下能够提高实现一致收敛的速度。

证明对（5）式两边进行拉普拉斯变换，可以得到特征方程det[sI+e-sτ(v1+v2βs)L]=0，利用网络拓扑的连通性，经过计算可以得到

从（6）式可以看出，s=0为其单根，当s≠0时，分析方程s+λie-τs(v1+v2βs)=0的根。

令s=pi+jqi，其中pi,qi∈ℝ和j2=-1，经过计算可得

于是，由（7）式进一步计算可得

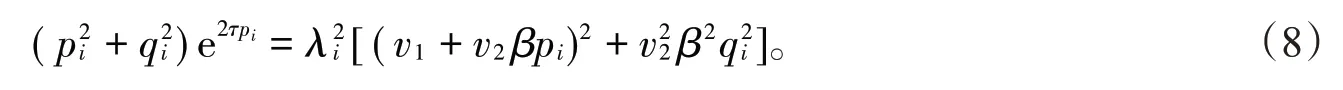
对（7）式两边关于β分别求导可得

和

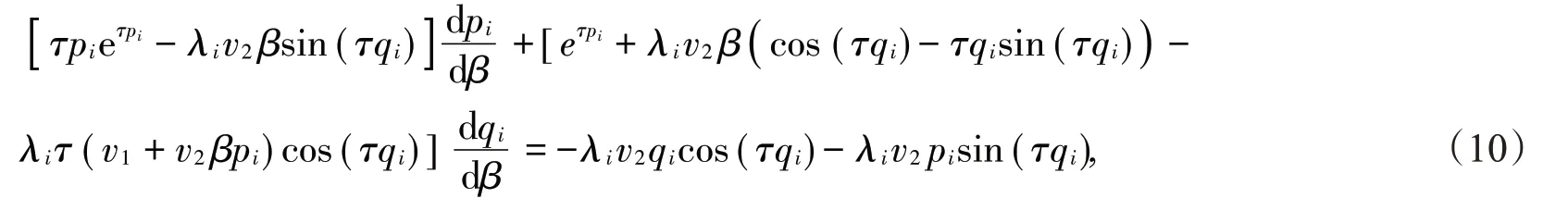
利用克莱姆法则得

由（7）式，将λi,β,v1,v2,τ看作常量，理论上可以求出pi=pi(β;λi,v1,v2,τ),qi=qi(β;λi,v1,v2,τ)，将此式代入到（11）式，可以求出但是，在一般情况下，很难求出的具体表达式，下面将考虑特殊情况下的符号。

实际上，由文献[11]可知，多智能体系统（1）在协议（3）下保证实现一致收敛的最大通讯时滞为τmax=且当τ=τimax时，pi=0，此时（7）、（8）式变为

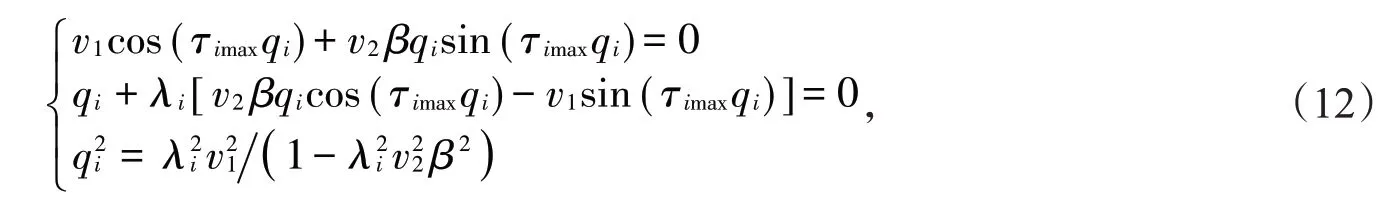
从（9）和（10）式入手，并利用克莱姆法则和（12）式可得：

上式进一步化简后得

所以Ψ(α)=0有且仅有一个解，记为，而且当时，Ψ(αi)＞0；当αi=α*i时，Ψ(αi)=0；当αi＞时 ，Ψ(αi)＜ 0。 由可知存在，使得且 当时 ，关于变量τ的连续性可知，存在使得对任意则对任意β∈(0,β*)和τ∈(τmax-,τmax)，有故当τ接近最大通讯时滞τ时，通过给定imax恰当强度的时滞状态导数反馈可以提高实现一致收敛的速度。

（2）通信时滞τ=0的情况

令τ=0，则（7）式变为

故当通讯时滞τ充分小时，对于带有任意强度的时滞状态导数反馈，减少了一致收敛的速度。

（3）超临界和亚临界时滞多智能体系统

设正函数V=V(p2,p3,…,pN)为多智能体系统的收敛速度，理论上将pi=pi(β;λi,τ,v1,v2)代入函数V可以得到收敛速度显示表达式V=V(p2(β;λi,τ,v1,v2),p3(β;λi,τ,v1,v2),…,pN(β;λi,τ,v1,v2) )，但是计算方式过于复杂，一般情况下无法使用该方法估计收敛速度。然而利用多智能体系统的收敛速度和闭环极点关系仍然可得，对于任意i∈{2 ,3,…,N}有由情况（1）和（2）的结论，并使用复合函数求导法则可知，当τ∈(0,τ0min)和β∈和β∈(0,β*)时。

综上所述，当多智能体系统（1）为超临界时滞多智能体系统时，引入时滞状态导数反馈可以提高实现一致收敛的速度；当多智能体系统（1）为亚临界时滞多智能体系统时，引入时滞状态导数反馈不能提高实现一致收敛的速度。

2 实例分析

考虑具有如下通信拓扑结构的多智能体系统，如图1所示，该系统的拉普拉斯阵为

在具有加权项的时滞状态导数反馈一致性协议（3）下，当通讯时滞τ=0.58 时，对于不同反馈强度β=0 和β=0.13，多智能体系统（1）仿真结果如图2 所示。从图2 可以看出，对于具有加权的时滞状态导数反馈的多智能体系统，假定通讯时滞τ=0.58，当反馈强度β=0时，图2(a)显示多智能体在t＞10后才能消除震荡；然而，当反馈强度β=0.13时，图2(b)显示多智能体在t＞5后就能消除震荡；当t=5时，利用所有智能体的状态与平均一致状态之间的误差函数可知，此时不同反馈强度下的误差为E(0.13)=0.040 1 ＜E(0)=0.256 2。因此引入适当反馈强度β=0.13可以有效提高多智能体系统实现一致性的收敛速度。

图1 多智能体系统的无向加权连通图

图2 多智能体系统应用协议（3）在τ=0.58 及不同反馈强度β=0 和β=0.13下的状态

3 总 结

研究发现，在无向通讯拓扑下，当一阶时滞多智能体系统具有加权项的时滞状态导数反馈协议时，通过对该系统闭环形式极点的讨论可以得出，超临界时滞多智能体系统必定存在恰当的反馈强度，使得系统（1）在一致协议（3）下能够有效提高实现一致收敛的速度。