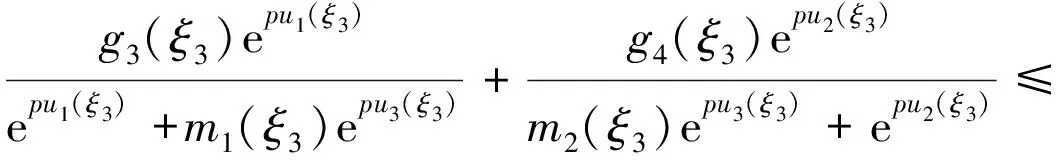比率型3种群混合模型正周期解的存在性

吴新民

(邵阳学院 理学院，湖南 邵阳，422000)

生态系统模型解的有界性、稳定性、振动性是种群动力系统中的重要研究内容，近几年有许多学者对此进行了比较深入和系统的研究，取得了有意义的结果[1-7]。本文考虑了如下一类比文献[1]更广泛的具有比率型的三种群混合模型:

(1)

这里xi(t)(i=1，2，3)表示t时刻Xi种群的密度；x1和x2为食饵种群；x3为捕食者种群；gi(t)(i=1，2，3)表示功能性反映函数；p≥1，为常数。并且假设模型中的系数ai(t)(i=1，2，3)，bi(t)，ci(t)，mi(t)(i=1，2)，gi(t)(i=1，2，3，4)均为正ω周期函数。

重合度理论在微分方程研究问题中有重要应用[8]，本文利用重合度的延拓定理，讨论了系统(1)中正ω周期解的存在性。所得结论是对文献[1]结果的实际性推广，因此，更具一般性和应用性。

1 预备知识

假设X，Z为两个Banach空间，线性算子L:DomL∩X→Z，现在定义2个投影算子，P:X∩DomL→X，Q:Z→Z/ImL，使得ImP=KerL，ImL=KerQ。

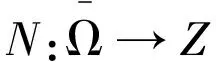
1)Lx≠λNx，∀x∈∂Ω∩DomL，λ∈(0，1);

2)QNx≠0，∀x∈∂Ω∩KerL;

3)deg{QNx，Ω∩KerL，0}≠0。

设f(t)为连续正ω周期函数，做如下定义：

2 结果及证明

定理1如果成立下列条件:

则系统(1)至少有1个正的ω周期解。

证明:设x1(t)=eu1(t)，x2(t)=eu2(t)，x3(t)=eu3(t)，则系统(1)变成

(2)

显然，系统(2)的ω周期解是系统(1)的正ω周期解。

令X=Y={(u1(t)，u2(t)，u3(t))T∈C(R，R3)，ui(t+ω)=ui(t)，i=1，2，3}

这里|Ω|代表R的欧几里得范数，由此X是1个Banach空间。又令：

其中：

DomL={(u1(t)，u2(t)，u3(t))T∈C′(R，R3)，N:X→Y}，

及

定义2个投影P和Q如下：

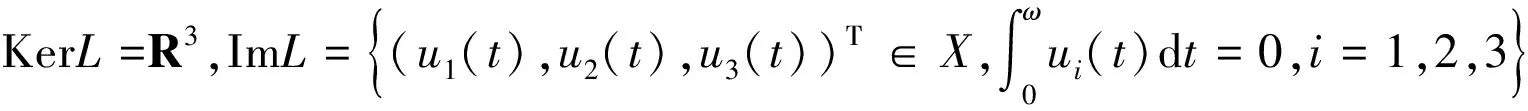
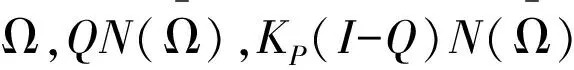
(3)

选择ξi，ηi∈[0，ω]，使得

则u′i(ξi)=u′i(ηi)=0，i=1，2，3，从这里和系统(3)有

(4)

(5)

(6)

和

(7)

(8)

(9)

从公式(4)中得到b1(ξ1)eu1(ξ1)

(10)

从公式(5)中得到c2(ξ2)eu2(ξ2)

(11)

即

因此有

(12)

从公式(7)中得到

即

(13)

同理从公式(8)中得

(14)

即

于是得到

(15)

由公式(10)～(15)，有

显然Ri(i=1，2，3)独立于λ。类似于前面的证法，能够证明当下列系统

(16)

有解时，它的每一解α*，β*，γ*满足

现在令

设系统(16)无解，则QNu≠(0，0，0)T。因此引理1的条件(2)是满足的。接下来证明引理1的条件(3)满足。作映射Ø:DomL×[0，1]→X

需证明当u∈∂Ω∩KerL，Ø(u1，u2，u3，μ)≠0，即Ø为一同伦映射。若结论不真，

即当u∈∂Ω∩R3，Ø(u1，u2，u3，μ)=0，于是由

利用公式(10)～(15)相类似的证明可得到

证明了Ω满足引理1的所有条件，由引理1知，系统(2)至少有1个ω周期解，定理1证毕。